Implementation of a Stirling number estimator enables direct calculation of population genetics tests for large sequence datasets

Abstract

Motivation

Stirling numbers enter into the calculation of several population genetics statistics, including Fu’s F_s. However, as alignments become large (≥50 sequences), the Stirling numbers required rapidly exceed the standard floating point range. Another recursive method for calculating Fu’s F_s suffers from floating point underflow issues.

Results

I implemented an estimator for Stirling numbers that has the advantage of being uniformly applicable to the full parameter range for Stirling numbers. I used this to create a hybrid Fu’s F_s calculator that accounts for floating point underflow. My new algorithm is hundreds of times faster than the recursive method. This algorithm now enables accurate calculation of statistics such as Fu’s F_s for very large alignments.

Availability and implementation

An R implementation is available at http://github.com/swainechen/hfufs.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Population genetics statistics are commonly used to test for evolutionary inference from sequence alignments. Well-known statistics include Tajima’s D (Tajima, 1989), Fay and Wu’s H (Fay and Wu, 2000) and Fu’s D and F (Fu and Li, 1993). Another statistic, Fu’s F_s (Fu, 1997), was recently shown to be potentially useful for identifying the causative mutation leading to a recent population expansion in the bacterium Campylobacter jejuni (Wu et al., 2016). There are several existing software packages that can calculate Fu’s F_s. However, some of these programs fail to calculate Fu’s F_s when alignments become too large, and others disagree on the value. I show that these issues are due to floating point overflow and underflow, respectively. I developed a hybrid algorithm to circumvent these computational issues. I demonstrate that this algorithm is hundreds of times faster than another recursive algorithm that is usable on large alignments. My algorithm may be useful for further testing the utility of Fu’s F_s on contemporary datasets, which can easily be in the hundreds to thousands of sequences.

2 Materials and methods

Fu’s F_s can be calculated from a multiple sequence alignment. One requires the number of alleles (denoted $k_0$⁠) and the mean number of pairwise nucleotide differences (denoted ${\widehat{\theta }}_{\pi }$⁠). The statistic $S\mathrm{\text{'}}$ is then defined as:

$$S^{\mathrm{\text{'}}}=\mathrm{ }\sum _{k\ge k_0}\frac{\left|S_k\right|{\widehat{\theta }}_{\pi }^k}{S_n{(\widehat{\theta }}_{\pi })}$$

(1)

where $S_n\left({\widehat{\theta }}_{\pi }\right)={\widehat{\theta }}_{\pi }\left({\widehat{\theta }}_{\pi }+1\right)\cdots \mathrm{(}{\widehat{\theta }}_{\pi }+n-1)$ and $S_k$ is the coefficient of ${\widehat{\theta }}_{\pi }^k$ in $S_n$ (Fu, 1997). The coefficients $S_k$ are also denoted in other literature as $S_n^{\left(k\right)}$⁠, where they are referred to as Stirling numbers of the first kind (Temme, 1993); hereafter I refer to these simply as Stirling numbers. Fu’s F_s is then defined as:

$$F_{\mathrm{s}}=\ln \left(\frac{S\mathrm{\text{'}}}{1-S\mathrm{\text{'}}}\right).$$

(2)

Stirling numbers can grow large very quickly, leading to floating point overflow. To circumvent this, I used the Stirling number estimator developed by Temme (1993) [Equation (3.5) therein]. The use of the logit transformation leads to floating point underflow when $S\mathrm{\text{'}}$ is close to 1. Further details of the theory and program details can be found in the Supplementary Material, including Equations (A1)–(A10).

3 Results

I used several software programs to calculate Fu’s F_s using the fimH dataset (Table 1). PopGenome and PGEToolbox gave the same results for all tests; only results for PopGenome are shown. PopGenome and PGEToolbox explicitly calculate Stirling numbers as part of the Fu’s F_s calculation; neither provides an answer when the Stirling numbers overflow the floating point range in R or Matlab (1.8e + 308). In contrast, DnaSP uses a recursive algorithm based on Equations (19)–(23) from Ewens (1972), avoiding calculation of Stirling numbers. However, the other programs disagreed at some values (bold in Table 1).

Table 1.

Fu’s F_s values calculated on subsets of fimH sequences

$n/k_0$	${\widehat{\theta }}_{\pi }$	Pop genome	DnaSP v5	DnaSP v6	Arlequin	hfufs	Bignum
5/5	7.80	−0.678	−0.678	−0.678	−0.678	−0.678	−0.678
10/9	7.69	−2.294	−2.294	−2.294	−2.294	−2.294	−2.294
25/20	9.39	−6.832	−6.832	−6.832	−6.832	−6.832	−6.832
50/31	9.61	−10.129	−10.129	−10.129	−10.129	−10.130	−10.129
100/40	9.37	−10.230	−10.230	−10.230	−10.230	−10.231	−10.230
250/67	8.96	NaN	−26.409	−26.410	−24.115	−26.409	−26.409
500/95	9.04	NaN	−47.06	−31.781	−23.964	−46.763	−46.763
1000/152	9.07	NaN	−112.627	−112.627	−23.718	−112.427	−112.427
2001/213	9.03	NaN	−192.343	−30.617	−23.596	−192.181	−192.181

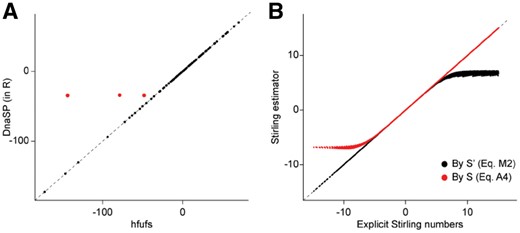
To reconcile the results, I implemented a Fu’s F_s calculator in R using the logarithmic Stirling number estimator (Temme, 1993). I also ported the Stirling number calculator from PGEToolbox and the recursive Fu’s F_s calculator from DnaSP v6. The limited range at low values of Fu’s F_s for DnaSP v6 is due to floating point underflow; because Fu’s F_s is calculated by Equation (A4), when the numerator is close to zero, two numbers close to 1 are subtracted, leading to a lower bound determined by machine precision (Fig. 1A). It occurs occasionally because the underflow test does not catch all cases (Table 1, bold underlined values for real data; Fig. 1A, red for simulated data). Arlequin suffers from a similar issue.

Fig. 1.

Validation of Fu’s Fs calculations. (A) Plot of Fu’s F_s calculated by the DnaSP V6 algorithm reimplemented in R versus the hfufs algorithm. Red dots indicate where underflow is not detected by the DnaSP code. (B) Plot of Fu’s F_s calculated using the Stirling number estimator versus using explicit Stirling numbers. Black dots calculated using Equation (2), red dots using Equation (A4). Dotted black lines are drawn at y=x

There are minor differences in Fu’s F_s values calculated by the different programs for ≥500 sequences (Table 1, bold bold values with no underlining). DnaSP v6 performs a second test for floating point underflow, in which case $S\mathrm{\text{'}}$ is estimated as $p\left(k_0\right)$ [Equation (A4)], leading to this discrepancy. To further confirm which values were correct, I reimplemented the PGEToolbox algorithm in perl using the bignum package for arbitrary precision mathematics; these explicit values agree with those obtained using the logarithmic Stirling number estimator.

For Fu’s F_s values <0, those calculated using a Stirling number estimator agree well with those calculated using explicit Stirling numbers (Fig. 1B, black dots). For high values of Fu’s F_s (where $S\mathrm{\text{'}}$ is close to 1), the range is limited again because of floating point underflow (⁠$1-S\mathrm{\text{'}}$ is limited by machine precision). This can be rectified by using Equation (A4) with the Stirling number estimator, which now agrees with values calculated using explicit Stirling numbers (Fig. 1B, red dots).

Therefore, the final algorithm (termed hfufs for hybrid Fu’s F_s) is:

1. Direct calculation of Fu’s F_s using Stirling numbers if the number of alleles is relatively small (⁠$n\le 30$⁠).

2. If n > 30, or there is overflow from direct calculation, then calculate Fu’s F_s using a Stirling number estimator.

3. If the value obtained is >0, then calculate Fu’s F_s using a Stirling number estimator by Equation (A4).

The DnaSP algorithm generally works well, but is recursive. I benchmarked my algorithm against the reimplemented DnaSP algorithm in R. R is notoriously slow for recursion, though caching of function results can help. I found that my algorithm was several hundred times faster [0.35 ± 0.09 s (for hfufs) compared with 162.65 ± 13.20 s for 100 calculations]. As expected, the recursive algorithm was far faster when rerun on the same parameter set (taking advantage of function caching for the recursive step; 0.89 ± 0.09 s for 100 calculations), but hfufs (which did not use caching) remained 2.5 times faster.

4 Conclusion

The hfufs algorithm solves issues with data size, floating point underflow and overflow, and accuracy in calculating Fu’s F_s. By avoiding recursion, it also improves speed. A software implementation in R is available at http://github.com/swainechen/hfufs.

Acknowledgements

I thank Shyam Prabhakar, Niranjan Nagarajan, Weiwei Zhai and the members of the Chen lab for useful discussions.

Funding

This work was supported by the National Medical Research Council, Ministry of Health, Singapore [grant numbers NMRC/CIRG/1357/2013, NMRC/CIRG/1467/2017]; and the Genome Institute of Singapore (GIS)/Agency for Science, Technology and Research (A*STAR).

Conflict of Interest: none declared.