A compositional mediation model for a binary outcome: Application to microbiome studies

Abstract

Motivation

The delicate balance of the microbiome is implicated in our health and is shaped by external factors, such as diet and xenobiotics. Therefore, understanding the role of the microbiome in linking external factors and our health conditions is crucial to translate microbiome research into therapeutic and preventative applications.

Results

We introduced a sparse compositional mediation model for binary outcomes to estimate and test the mediation effects of the microbiome utilizing the compositional algebra defined in the simplex space and a linear zero-sum constraint on probit regression coefficients. For this model with the standard causal assumptions, we showed that both the causal direct and indirect effects are identifiable. We further developed a method for sensitivity analysis for the assumption of the no unmeasured confounding effects between the mediator and the outcome. We conducted extensive simulation studies to assess the performance of the proposed method and applied it to real microbiome data to study mediation effects of the microbiome on linking fat intake to overweight/obesity.

Availability and implementation

An R package can be downloaded from https://github.com/mbsohn/cmmb.

Supplementary information

Supplementary files are available at Bioinformatics online.

1 Introduction

The human microbiome is recognized as a key determinant of normal physiology and immune homeostasis (Li, 2015; Honda and Littman, 2016; Thaiss et al., 2016). Essential functions provided by the microbiome include the regulation of the immune system and metabolic function, the synthesis of essential vitamins, and the removal of toxic compounds (Heintz-Buschart and Wilmes, 2018). It has also been shown that the microbiome changes readily in response to extrinsic factors, such as diet and xenobiotics (Wu et al., 2011; Lewis et al., 2015; Kurilshikov et al., 2017). This dual role of the microbiome is very appealing in biomedical science, as it can be used as a non-invasive therapeutic application. Modulating targeted microbes using xenobiotics, for instance, would be more effective than imposing a complete dietary change for obesity treatment and could be as effective as bariatric surgery with no severe side effects. To translate the microbiome research into therapeutic and preventative applications, however, we need to understand mechanisms underlying the effect of external factors or interventions on the disease transmitted through the perturbation in the microbiome.

Mediation analysis, which studies the effect of treatment on outcome transmitted through a variable called a mediator, has been widely applied in numerous disciplines, such as sociology and epidemiology. It traditionally has been formulated and implemented under the structural equation modeling (SEM) framework (Baron and Kenny, 1986; MacKinnon et al., 2002); however, with recent advances in causal inference, which clarifies the assumptions needed for causal interpretation, mediation analysis under the potential outcomes (PO) framework has been gaining popularity (Pearl, 2001; Rubin, 2005; Imai et al., 2010; VanderWeele and Vansteelandt, 2010). Recent studies have extended the traditional single-mediator model to the multiple-mediators model (Imai and Yamamoto, 2013; VanderWeele and Vansteelandt, 2014), even in high-dimensional settings (Chén et al., 2015; Huang and Pan, 2016; Zhao and Luo, 2016). These mediation models, however, are not directly applicable for microbiome data due to the compositional nature of the microbiome data.

Compositional data comprise the proportions or percentages of a whole, imposing a unit-sum constraint, i.e. the sum of components is 1 or 100%. This unit-sum constraint makes a composition with k-components lie in the $(k-1)$-dimensional simplex space ${\mathbb{S}}^{k-1}$ and makes it impossible to alter one component without altering at least one of the other components. Neglecting this compositional structure thus can cause undesirable consequences. Sohn and Li (2019) proposed a sparse compositional mediation model (CMM) for continuous outcomes under the PO framework utilizing the algebra defined in the simplex space (Aitchison, 1986; Billheimer et al., 2001) and a linear constraint on regression coefficients, which is a necessary condition to satisfy the basic properties of compositional data, such as scale and permutation invariance (Aitchison and Bacon-Shone, 1984; Lin et al., 2014). Subsequently, a few compositional mediation methods for continuous outcomes have been proposed (Wang et al., 2020; Zhang et al., 2021). In many human microbiome studies, however, the outcome is binary, such as the presence or absence of disease.

In this article, we extend CMM to accommodate binary outcomes. The effect of a treatment on all the components of a compositional mediator is jointly estimated using the algebra in the simplex space. For the quantification of the effects of a treatment and a compositional mediator on binary outcomes, an L1-penalized probit model with a linear constraint is used. Its parameters are estimated by an algorithm that combines the iteratively reweighted least-squares (IRLS) (Green, 1984; Lee et al., 2006) and the coordinate descent method of multipliers (CDMM) (Lin et al., 2014). To obtain asymptotically unbiased estimates for the parameters of the L1-penalized probit model, we developed a debias procedure that extends the methods of Shi et al. (2016) and Lu et al. (2019). We defined an estimator for the mediation effect under the PO framework and evaluated its performance in extensive simulation settings. We also developed a method for sensitivity analysis for the assumption of the no unmeasured confounding effects between the mediator and the outcome. We applied CMM to a real dataset, COMBO (Wu et al., 2011), to link diet fat intake to overweight/obesity and found a significant effect of fat intake on overweight/obesity mediated through the gut microbiome.

2 Materials and methods

2.1 Algebraic operators in simplex space

We first provide the definitions of the algebraic operators in the simplex space that appear in this article. For two compositions of k-components $\mathit{\eta },\mathit{\zeta }\in {\mathbb{S}}^{k-1}$⁠, the perturbation operator is defined as

$$\mathit{\eta }\oplus \mathit{\zeta }={({\eta }_1{\zeta }_1/\sum _{j=1}^k{\eta }_j{\zeta }_j,\dots ,{\eta }_k{\zeta }_k/\sum _{j=1}^k{\eta }_j{\zeta }_j)}^{\top };$$

the inverse of the perturbation operator as

$$\mathit{\eta }\ominus \mathit{\zeta }={({\eta }_1{\zeta }_1^{-1}/\sum _{j=1}^k{\eta }_j{\zeta }_j^{-1},\dots ,{\eta }_k{\zeta }_k^{-1}/\sum _{j=1}^k{\eta }_j{\zeta }_j^{-1})}^{\top };$$

the power transformation for a composition $\mathit{\eta }$ by a scalar $\upsilon$ as

$${\mathit{\eta }}^{\upsilon }={({\eta }_1^{\upsilon }/\sum _{j=1}^k{\eta }_j^{\upsilon },\dots ,{\eta }_k^{\upsilon }/\sum _{j=1}^k{\eta }_j^{\upsilon })}^{\top };$$

and a norm for composition as

$$\Vert \mathit{\eta }\Vert ={({\mathit{\eta }}^T\mathit{\eta })}^{1/2}={(\text{alr}{(\mathit{\eta })}^T{\mathcal{N}}^{-1}\text{alr}(\mathit{\eta }))}^{1/2},$$

where $\text{alr}(·)$ is the additive log-ratio transformation and ${\mathcal{N}}^{-1}$ is the inverse matrix of a $(k-1)\times (k-1)$ matrix $\mathcal{N}={\mathcal{I}}_{k-1}+1_{k-1}{1}_{k-1}^T$ (Aitchison, 1986; Billheimer et al., 2001).

2.2 Compositional mediation model for binary outcomes

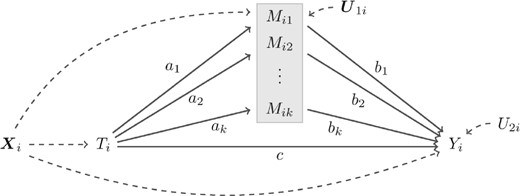
Suppose that we have n random samples from a population, where we observe an outcome Y_i, a compositional mediator ${\mathit{M}}_i$⁠, a treatment T_i, and covariates ${\mathit{X}}_i$ for $i=1,\dots ,n$⁠, and that we consider an expected causal effect of T_i on Y_i mediated through ${\mathit{M}}_i$⁠, depicted in Figure 1. Then, a model for this mediation effect should take the compositional nature of ${\mathit{M}}_i$ into an account, as ${\mathit{M}}_i\in {\mathbb{S}}^{k-1}$⁠. To develop such a model, we utilize algebraic operations defined in the simplex space and a zero-sum constraint on regression coefficients for the components of a composition.

Fig. 1.

A compositional mediation model: a_j, b_j, and c are path coefficients, $j=1,\dots ,k$⁠; ${\mathit{U}}_{1i}$ and $U_{2i}$ are disturbance terms for k compositional mediators ${\mathit{M}}_i$ and an outcome Y_i, respectively; T_i is a treatment variable; ${\mathit{X}}_i$ is a set of pretreatment covariates

With the perturbation and power transformation operators, the proposed compositional mediation model for a binary outcome (CMM) is given by

$${\mathit{M}}_i=({\mathit{m}}_0\oplus {\mathit{a}}^{T_i}\underset{r=1}{\overset{n_x}{\oplus }}{\mathit{h}}_r^{X_{ri}})\oplus {\mathit{U}}_{1i}$$

(1)

 

$$\begin{array}{c}{Y}_i=1\{c_0+c{T}_i+{\mathit{b}}^{\top }(\text{log}\hspace{0.17em}{\mathit{M}}_i)+{\mathit{g}}^{\top }{\mathit{X}}_i+U_{2i}>0\},\\ \text{subject}\text{to}{1}_k^{\top }\mathit{b}=0,\end{array}$$

(2)

where ${\mathit{m}}_0$ is a baseline composition (i.e. when $T_i=\mathbb{E}(T_i)$⁠); c₀ a baseline measure for Y_i; a a vector of composition parameters for a treatment; c regression coefficients for the treatment; b regression coefficients for the composition; ${\mathit{h}}_1,\dots ,{\mathit{h}}_{n_x}$ and g nuisance parameters corresponding to ${\mathit{X}}_i$⁠; ${\mathit{U}}_{1i}$ and $U_{2i}$ disturbance terms for ${\mathit{M}}_i$ and Y_i, respectively; and $\underset{r=1}{\overset{n_x}{\oplus }}{\mathit{\eta }}_r={\mathit{\eta }}_1\oplus \cdots \oplus {\mathit{\eta }}_{n_x}$⁠. We assume ${\mathit{U}}_{1i}$ follows a logistic normal distribution with mean $0$ and covariance Σ and $U_{2i}$ follows a standard normal distribution. Model (1) formulates the effect of a treatment on a compositional mediator perturbed from the baseline composition, which is measured by the parameter a, after adjusting for pretreatment covariates, and Model (2) links treatment and a compositional mediator to a binary outcome after adjusting for pretreatment covariates while it accounts for the compositional nature of ${\mathit{M}}_i$ by imposing a zero-sum constraint, ${\mathit{b}}^{\top }{1}_k=0$⁠. Note that the vector of regression coefficients b is scale-invariant with respective to ${\mathit{M}}_i$ because of the zero-sum constraint, i.e. ${(\text{log}\hspace{0.17em}C{\mathit{M}}_i)}^{\top }\mathit{b}={(\text{log}\hspace{0.17em}{\mathit{M}}_i)}^{\top }\mathit{b}$ for any constant C.

2.3 Model assumptions and identification

As in most of the work on causal mediation analysis, estimators of the natural direct and indirect (or mediation) effects for the proposed method are defined under the causal assumptions: the stable unit treatment value assumption (SUTVA) (Imbens and Rubin, 2015), the positivity assumption, and the no-unmeasured confounding assumption, i.e. a set of pretreatment covariates is sufficient to control for confounding effects. See Supplementary Material D.3 for details of these assumptions. Suppose that Models (1) and (2) are correctly specified. Then, under these assumptions, the direct effect $\zeta (t)$ and the total indirect effect $\delta (t)$ are identifiable and given by

$$\begin{array}{c}\zeta (\tau )\equiv \mathbb{E}\left[Y_i(t,\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{M}}_i(\tau ))-Y_i(t\prime ,\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{M}}_i(\tau ))|{\mathit{X}}_i=\mathit{x}\right]\\ =\mathbb{E}\left\{\Phi \left(\frac{ct+f_{\zeta }(\tau ,{\mathit{X}}_i)}{\sqrt{{\mathit{b}}_{-k}^{\top }\Sigma {\mathit{b}}_{-k}+1}}\right)-\Phi \left(\frac{ct\prime +f_{\zeta }(\tau ,{\mathit{X}}_i)}{\sqrt{{\mathit{b}}_{-k}^{\top }\Sigma {\mathit{b}}_{-k}+1}}\right)\right\},\end{array}$$

 

$$\begin{array}{c}\delta (\tau )\equiv \mathbb{E}\left[Y_i(\tau ,\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{M}}_i(t))-Y_i(\tau ,\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{M}}_i(t\prime ))|{\mathit{X}}_i=\mathit{x}\right]\\ =\mathbb{E}\{\Phi \left(\frac{{(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}t+f_{\delta }(\tau ,{\mathit{X}}_i)}{\sqrt{{\mathit{b}}_{-k}^{\top }\Sigma {\mathit{b}}_{-k}+1}}\right)\\ -\Phi \left(\frac{{(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}t\prime +f_{\delta }(\tau ,{\mathit{X}}_i)}{\sqrt{{\mathit{b}}_{-k}^{\top }\Sigma {\mathit{b}}_{-k}+1}}\right)\},\end{array}$$

where t is an observed treatment, $t\prime$ a reference value for the treatment, $f_{\zeta }(\tau ,\mathit{x})=c_0+{\mathit{b}}^{\top }(\text{log}\hspace{0.17em}{\mathit{m}}_0+\tau \hspace{0.17em}\text{log}\hspace{0.17em}\mathit{a}+{\sum }_{r=1}^{n_x}{x}_r\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{h}}_r)+{\mathit{g}}^{\top }\mathit{x}$⁠, and $f_{\delta }(\tau ,\mathit{x})=c_0+c\tau +{\mathit{b}}^{\top }(\text{log}\hspace{0.17em}{\mathit{m}}_0+{\sum }_{r=1}^{n_x}{x}_r\hspace{0.17em}\text{log}\hspace{0.17em}{\mathit{h}}_r)+{\mathit{g}}^{\top }\mathit{x}$⁠. Note that these estimators, $\zeta (\tau )$ and $\delta (\tau )$⁠, are invariant to the order of components (taxa) because of the constraint on a (i.e. lies in the simplex space) and the zero-sum constraint of b (i.e. $1_k^{\top }\mathit{b}=0$⁠).

2.4 Estimation of composition parameters

To estimate the parameters in Model (1), we minimize the difference between observed and estimated compositions in ${\mathbb{S}}^{k-1}$⁠. With the operators in ${\mathbb{S}}^{k-1}$⁠, we solve the following optimization problem:

$$\widehat{\mathbf{\theta }}=\underset{{\mathit{m}}_0,\mathit{a},{\mathit{h}}_r\in {\mathbb{S}}^{k-1}}{\text{argmin}}\sum _{i=1}^n{\Vert {\mathit{M}}_i\ominus \left({\mathit{m}}_0\oplus {\mathit{a}}^{T_i}\underset{r=1}{\overset{n_x}{\oplus }}{\mathit{h}}_r^{X_{ri}}\right)\Vert }^2,$$

(3)

where ${\widehat{\theta }}^{\top }=({\widehat{m}}_0,\widehat{a},{\widehat{h}}_1,\dots ,{\widehat{h}}_{n_x})$⁠. The objective function in (3) is convex in terms of $\text{alr}({\mathit{m}}_0),\hspace{0.17em}\text{alr}(\mathit{a})$⁠, and $\text{alr}({\mathit{h}}_r)$ for $r=1,\dots ,n_x$⁠, and the estimators are consistent and unbiased estimators. See Supplementary Material A for details.

2.5 Estimation of regression parameters

To estimate the parameters of the composition in Model (2), we will use a log-contrast model. Let ${\eta }_i=2y_i-1,\hspace{0.17em}{\mathit{z}}_i={(1,t_i,\hspace{0.17em}\text{log}\hspace{0.17em}{({\mathit{m}}_i)}^{\top },{\mathit{x}}_i^{\top })}^{\top },\hspace{0.17em}\mathit{\beta }={(c_0,c,{\mathit{b}}^{\top },{\mathit{g}}^{\top })}^{\top }$⁠, and $q({\eta }_i{\mathit{z}}_i^{\top }\mathit{\beta })=-\text{log}\hspace{0.17em}\Phi ({\eta }_i{\mathit{z}}_i^{\top }\mathit{\beta })$⁠. Then, the L₁ penalized log-likelihood function for Model (2) is given by

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{n}\sum _{i=1}^{n}q({\eta }_i{\mathit{z}}_i^{\top }\mathit{\beta })\right\},\hspace{0.17em}\hspace{0.17em}\text{subject}\text{to}\left|\right|\mathit{\beta }|{|}_1\le t;\hspace{0.17em}{1}_k^{\top }\mathit{b}=0,$$

where $t\ge 0$ is some constant. The solution of this optimization problem is equivalent to the solution of the following optimization problem:

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{2n}\left|\right|{\Xi }^{1/2}(\mathit{u}-Z\mathit{\beta })|{|}_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1\right\};\hspace{0.17em}{1}_k^{\top }\mathit{b}=0,$$

(4)

where Ξ is an n × n diagonal matrix with its ith diagonal term ${\Xi }_{ii}={\xi }_i({\eta }_i{\mathit{z}}_i^{\top }{\mathit{\beta }}^{*})[{\mathit{z}}_i^{\top }{\mathit{\beta }}^{*}+{\xi }_i({\eta }_i{\mathit{z}}_i^{\top }{\mathit{\beta }}^{*})]$⁠; ${\mathit{\beta }}^{*}$ a vector lying between ${\mathit{\beta }}_0$ and $\mathit{\beta }$⁠; ${\xi }_i(\mathit{\beta })={\eta }_i\varphi ({\eta }_i{\mathit{z}}_i^{\top }\mathit{\beta })/\Phi ({\eta }_i{\mathit{z}}_i^{\top }\mathit{\beta })$⁠; $\mathit{\xi }({\mathit{\beta }}_0)={({\xi }_1({\mathit{\beta }}_0),\dots ,{\xi }_1({\mathit{\beta }}_0))}^{\top }$⁠; $Z={({\mathit{z}}_1,\dots ,{\mathit{z}}_n)}^{\top }$⁠; $\mathit{u}=Z{\mathit{\beta }}_0+{\Xi }^{-}\mathit{\xi }({\mathit{\beta }}_0)$⁠; and $\lambda \ge 0$ is a penalty term. Letting $\tilde{Z}=Z({\mathcal{I}}_p-\mathit{\iota }{\mathit{\iota }}^{\top }/k)$⁠, where ${\mathit{\iota }}^{\top }=(0,0,1_k^{\top },0,\dots ,0)$⁠, Equation (4) can be written as

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{2n}\left|\right|{\Xi }^{1/2}(\mathit{u}-\tilde{Z}\mathit{\beta })|{|}_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1\right\},\hspace{0.17em}{\mathit{\iota }}^{\top }\mathit{\beta }=0.$$

(5)

We need this transformation of Z for the debiasing procedure in the following section. Note that the solutions of Equations (4) and (5) are the same since ${\mathit{\iota }}^{\top }\mathit{\beta }=0$⁠. The objective function in Equation (5) has the form of weighted least squares; however, Ξ and u depend on unknown quantities, ${\mathit{\beta }}^{*}$ and ${\mathit{\beta }}_0$⁠, respectively. Therefore, we propose a method that combines iteratively reweighted least squares and coordinate descent method of multipliers (IRLS-CDMM), which iteratively updates ${\Xi }^{(\ell )}$ and ${\mathit{u}}^{(\ell )}$⁠. The algorithm for IRLS-CDMM consists of constructing the augmented Lagrangian,

$$L_{\mu }=\frac{1}{2n}\left|\right|{\Xi }^{1/2}(\mathit{u}-\tilde{Z}\mathit{\beta })|{|}_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1+\varsigma {\mathit{\iota }}^{\top }\mathit{\beta }+\frac{\mu }{2}{({\mathit{\iota }}^{\top }\mathit{\beta })}^2,$$

where ς is the Lagrange multiplier and $\mu >0$ a penalty parameter; and iterative updates of

$${\mathit{\beta }}^{(\ell +1)}\leftarrow \underset{\beta }{\text{argmin}}{L}_{\mu }(\mathit{\beta },{\Xi }^{\left(\ell \right)},{\mathit{u}}^{\left(\ell \right)},{\gamma }^{\left(\ell \right)}),{\Xi }^{(\ell +1)}\leftarrow \underset{{\beta }^{*}}{\text{argmin}}\sum _{i=1}^{n}q({\eta }_i{\tilde{\mathit{z}}}_i^{\top }{\mathit{\beta }}^{*}),{\mathit{u}}^{(\ell +1)}\leftarrow \tilde{Z}{\mathit{\beta }}^{(\ell +1)}+{\Xi }^{-(\ell +1)}\mathit{\xi }({\mathit{\beta }}^{(\ell +1)}),{(\varsigma /\mu )}^{(\ell +1)}\leftarrow {(\varsigma /\mu )}^{(\ell )}+{\mathit{\iota }}^{\top }\mathit{\beta }.$$

The details of this algorithm are provided in Supplementary Material B.

2.6 Debiasing procedure and its asymptotic convergence

The solution $\widehat{\mathit{\beta }}$ of Equation (5) is biased because of L₁ penalization. To correct this bias, we adapt the debiased procedure of Shi et al. (2016) and Lu et al. (2019). The proposed de-biased estimator of $\widehat{\mathit{\beta }}$ given $\widehat{\Xi }$ and $\widehat{\mathit{u}}$ is given by

$${\widehat{\mathit{\beta }}}_{db}=\widehat{\mathit{\beta }}+\frac{1}{n}\tilde{\Theta }{\tilde{Z}}^{\top }\widehat{\Xi }(\widehat{\mathit{u}}-\tilde{Z}\widehat{\mathit{\beta }}),$$

(6)

where $\tilde{\Theta }=({\mathcal{I}}_p-\mathit{\iota }{\mathit{\iota }}^{\top }/k)\widehat{\Theta }$ and $\widehat{\Theta }={({\widehat{\mathit{\theta }}}_1,\dots ,{\widehat{\mathit{\theta }}}_p)}^{\top }$ is a solution of the following convex problem,

$${\widehat{\mathit{\theta }}}_j=\min {\mathit{\theta }}_j^{\top }\widehat{\Sigma }{\mathit{\theta }}_j\hspace{0.17em}\mathrm{s}.\mathrm{t}.\left|\right|\widehat{\Sigma }{\mathit{\theta }}_j-({\mathcal{I}}_p-\mathit{\iota }{\mathit{\iota }}^{\top }/k){\mathit{e}}_j|{|}_{\infty }\le \gamma ,$$

where $j=1,\dots ,p,\hspace{0.17em}\widehat{\Sigma }={\tilde{Z}}^{\top }\widehat{\Xi }\tilde{Z}/n,\hspace{0.17em}{\mathit{e}}_j\in {\mathbb{R}}^p$ the vector with one at the jth position and zero everywhere else, and γ some constant. Under some regularity conditions, the debiased estimator ${\widehat{\mathit{\beta }}}_{db}$ converges to $\mathit{\beta }$ as $n,p\to \infty$⁠. The algorithm for the debiasing procedure and the asymptotic properties of the debiased estimators are given in Supplementary Materials C and D.

2.7 Hypothesis test of mediation effect

The distribution of the total mediation effect $\delta (\tau )$ is unknown, so we propose a bootstrap approach to test the significance of an expected causal mediation effect,

$$H_0:\delta (\tau )=0\hspace{1em}\text{vs}.\hspace{1em}{\mathrm{H}}_1:\delta (\tau )\ne 0.$$

(7)

To construct a sampling distribution of $\delta (\tau )$⁠, we repeat the following steps B times: (i) randomly select n samples from the original n samples with replacement, and (ii) estimate ${\delta }_b(\tau )$⁠. We use the 95% percentile confidence interval to test the significance of $\delta (\tau )$ in this study. Alternatively, we can estimate an approximate P-value for $\delta (\tau )$ utilizing the fact that any bootstrap replicate $\delta {(\tau )}_b-\delta (\tau )$ should have a distribution close to that of $\delta (\tau )$ when the null hypothesis is true, where $\delta {(\tau )}_b$ denotes an estimated indirect effect derived from a bootstrap sample (Efron and Tibshirani, 1994).

2.8 Sensitivity analysis

In mediation analysis, the assumption of no unmeasured confounding effects is not verifiable. Particularly, no unmeasured confounding effects between a mediator and an outcome cannot be assured even in a randomized experiment, thus rendering estimated mediation effects prone to be biased. To address this potential problem, we propose a method for sensitivity analysis that extends the method proposed by Imai et al. (2010). Let $\rho \equiv \text{Corr}(\text{alr}{({\mathit{U}}_{1i})}_j,U_{2i})$ be a correlation between the disturbance terms for the compositional mediator and the outcome, respectively for all $j=1,\dots k-1$ and $Y_i=1\{{\tilde{c}}_0+\tilde{c}{T}_i+{\tilde{\mathit{g}}}^{\top }{\mathit{X}}_i+U_{0i}>0\}$ be a probit regression model for the total effect of T on Y. Suppose that the model assumptions are satisfied and the models are correctly specified. Then, for a given correlation ρ, we can identify the expected total mediation effect using

$${\delta }_{\rho }(\tau )=\mathbb{E}\{\Phi \left({\tilde{f}}_{\delta }(\tau )+\frac{{(\text{log}\hspace{0.17em}\mathit{a})}^{\top }{\mathit{b}}_{\rho }(t-\tau )}{\Psi (\mathit{\rho },{\mathit{b}}_{\rho },\Sigma )}\right)-\Phi \left({\tilde{f}}_{\delta }(\tau )+\frac{{(\text{log}\hspace{0.17em}\mathit{a})}^{\top }{\mathit{b}}_{\rho }(t\prime -\tau )}{\Psi (\mathit{\rho },{\mathit{b}}_{\rho },\Sigma )}\right)\},$$

(8)

where ${\tilde{f}}_{\delta }(\tau )={\tilde{c}}_0+\tilde{c}\tau +{\tilde{\mathit{g}}}^{\top }{\mathit{x}}_i,\hspace{0.17em}{\mathit{b}}_{\rho }$ is an adjusted estimate given ρ, and $\Psi (\mathit{\rho },{\mathit{b}}_{\rho },\Sigma )={\left[{({\mathit{b}}_{\rho })}_{-k}^{\top }\Sigma {({\mathit{b}}_{\rho })}_{-k}+2\rho {({\mathit{b}}_{\rho })}_{-k}^{\top }\text{diag}{(\Sigma )}^{1/2}+1\right]}^{1/2}$⁠. We can estimate ${\mathit{b}}_{\rho }$ utilizing the correlation between $U_{0i}$ and $\text{alr}{({\mathit{U}}_{1i})}_j$⁠. Note the range of ρ is not from −1 to 1 when the number of components is more than one since the components are not independent of each other, and its range becomes narrower as the number of components increases. See Supplementary Material E for details.

3 Results

3.1 Simulation study I: synthetic data

Mediation analysis for multiple or high-dimensional mediators often assumes independence between mediators. One approach to satisfying this assumption is to use principal components (PCs) of mediators, i.e. PCs of $\text{log}(M)$ as mediators. We use this approach under structural equation modeling (hereinafter referred to as PCS) and under the potential outcomes framework (PCP) to evaluate the performance of CMM. The main difference between these two approaches is how to estimate the direct and indirect effects: for PCS, the inner product of path coefficients (i.e. $\text{log}\hspace{0.17em}{(\mathit{a})}^{\top }\mathit{b}$⁠) was used for the indirect effect; and for PCP, an expression derived from the mediation formula was used (Pearl, 2001; Imai et al., 2010), which is like the expression for $\delta (\tau )$⁠.

In data generation, we randomly generated a treatment T_i from a Bernoulli distribution with success probability 0.5; a compositional disturbance ${\mathit{U}}_{1i}$ from a multivariate logistic normal (LN) distribution (Aitchison, 1986) with mean $0$ and covariance $\mathcal{N}$⁠; a regression disturbance $U_{2i}$ from a standard normal distribution, where $i=1,\dots ,50$⁠. We fixed $\mathit{a}={(20,10,5,2,1_{k-4}^{\top })}^{\top }/(20,10,5,2,1_{k-4}^{\top })1_k,\hspace{0.17em}\mathit{b}={(0.5,-0.5,0.5,-0.5,0_{k-4}^{\top })}^{\top }$⁠, and c = 1 for k = 5, 25, 50. For a baseline composition, ${\mathit{m}}_0=1_k/k$ was used. A composition ${\mathit{M}}_i$ and an outcome Y_i were then generated according to Models (1) and (2), respectively. Throughout the simulation studies and a real data application, we tested the direct and indirect effects at the 95% confidence level.

We first compared the coverage rate for the indirect effect, which measures a proportion of the time that estimated intervals contain the true value of an indirect effect. To this end, we first generated ${(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}\times r$ in each repetition, where r is randomly generated from the standard uniform distribution. In this setting, the true or known value of the total indirect effect is between 0 and 0.14. We then constructed a bootstrap confidence interval (CI) with 2000 bootstrap samples and measured the coverage rate for each method with each k. Figure 2 shows the results of 100 repetitions for each k. CMM yields the coverage rate around the nominal coverage rate (i.e. 0.95) for all the values of k considered. PCS gives the coverage rate around 0.95 when k = 5 but has an upward trend along with increased k. The coverage rate of PCP is a little lower than the nominal coverage rate for all k considered.

Fig. 2.

Coverage probabilities for the indirect effect estimated by CMM, PCP, and PCS for different numbers of taxa k

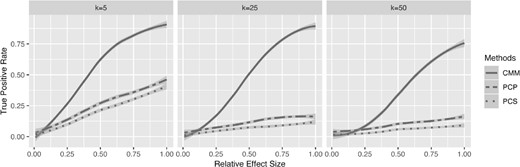
The second measure we used in performance comparison is the true positive rate versus the relative effect size, ${(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}\times r$⁠. Instead of randomly generating r, we increased r from 0 to 1 by 0.01 and calculated the true positive rate at a given r, which reflects a relative effect size of ${(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}$⁠. For each value of r, we used 100 repetitions. As shown in Figure 3, CMM outperforms PCP and PCS, even in a low dimensional setting (i.e. k = 5).

Fig. 3.

True positive rate versus relative effect size for CMM, PCP, and PCS and for different numbers of taxa k

We also compared the power and the size of these methods with n = 100 and k = 200. In this setting, we fixed r = 1 and estimated the total mediation effects and their bootstrap CIs. Based on 1000 and 500 simulations for the size and the power, all the methods control type I errors (CMM = 0.00, PCP = 0.01, and PCS = 0.01), but similar to the results with smaller k, CMM had a much higher power compared to the other methods (CMM = 0.73, PCP = 0.03, and PCS = 0.03).

3.2 Simulation study II: real microbiome data

To make a simulation setting more realistic, we used the composition of taxa in a real dataset, referred to as the ‘COMBO’ data (Wu et al., 2011), which was analyzed in Section 5.1. We first randomly permuted T_i and Y_i to measure the empirical size at $\alpha =0.05$⁠. For the power, we randomly generated T_i from N(0, 1) and estimated a with the Dirichlet regression (Maier, 2014). We then located the two largest and two smallest values of a and set $b_j=0.5$ if $j\in \{a_{(k)},a_{(k-1)}\},\hspace{0.17em}{b}_j=-0.5$ if $j\in \{a_{(1)},a_{(2)}\}$⁠, and b_j = 0 otherwise, where the subscript $(j)$ indicates the jth order. The direct effect c was set to 1, and Y_i was generated by the probit regression model (2). The estimated ${(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}$ in this setting was 0.29 ± 0.14. As PCP had a slightly better performance than PCS, we included only PCP in comparison.

As shown in Table 1, both PCP and CMM roughly control type I errors and have comparable powers for the direct effect. However, PCP has very low power to detect the total indirect effect, which is similar to the results in Section 3.1.

Table 1.

Power and size in testing DE and IDE: n = 96 and k = 45

	Power		Size
$\alpha =0.05$	DE	IDE	DE	IDE
CMM	0.900	0.942	0.066	0.004
PCP	0.810	0.222	0.051	0.001

The 1000 and 500 simulations were used for size and power, respectively.

3.3 Real data analysis: COMBO data

We applied CMM to the COMBO data, which consists of 16S rRNA gene sequences from fecal samples of 96 healthy individuals. It also contains demographic and clinical information including fat intake and BMI. Operational taxonomic units (OTUs) were summarized at the genus level, and the genera that appear in smaller than 10% of the samples were excluded, leaving 45 genera in 96 samples for analysis. Because of the compositional nature, the OTU counts assigned to the genera were transformed into proportions after adding a small number (0.5) to avoid the log-transformation of zero proportions, which is a common practice in compositional data analysis (Aitchison, 1986).

We dichotomized BMI at 25, which is generally used to define being normal (BMI < 25) or overweight/obese (BMI $\ge$ 25), and tested if the total effect of fat intake on overweight/obesity was statistically significant. The total calorie intake was included in the model as a pretreatment covariate. The estimated total effect with a probit model (i.e. $Y_i=1\{{\tilde{c}}_0+\tilde{c}{T}_i+\tilde{g}{X}_i+U_{0i}>0\}$⁠) was 0.122 with a 95% bootstrap CI of (0.017, 0.247). In other words, fat intake has a positive effect on overweight/obesity. CMM was then applied to study a mechanism of the effect of fat intake on overweight/obesity, in which the 45 genera were included as the components of a compositional mediator. The estimated direct effect was 0.018 with a CI of (−0.003, 0.073) and the estimated indirect effect was 0.030 with a CI of (0.000, 0.113), indicating positive mediation effects of fat intake on overweight/obesity.

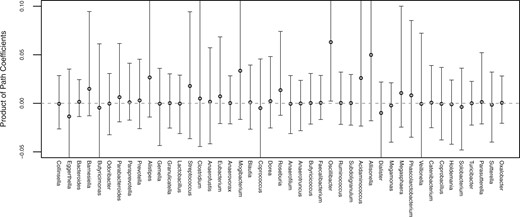
To estimate component-wise mediation effects, we need to know the distribution of $\text{log}\hspace{0.17em}{({\mathit{U}}_{1i})}_j$ for $j=1,\dots ,k$⁠; however, it is not attainable even though we know a distribution of $\text{alr}{({\mathit{U}}_{1i})}_j$ for $j=1,\dots ,k-1$⁠. Thus, we assessed the product of path coefficients instead to identify potential component-wise mediation effects, as it is directly related to component-wise mediation effect. The genus Oscillibacter was identified as a potential mediator: its estimated product of path coefficients was 0.062 with a 95% bootstrap CI of (0.002, 0.185). In previous studies, Oscillibacter-like organisms have been identified as a potentially important gut microbe that mediates high fat-induced gut dysfunction and permeability, and it has been shown that a decrease of Oscillibacter led to an increase in gut permeability, which was shown to be associated with obesity (Lam et al., 2012; Teixeira et al., 2012). The estimated products of path coefficients for other components and their 95% bootstrap CIs are shown in Figure 4.

Fig. 4.

Estimated products of path coefficients closely related to the component-wise mediation effects of fat intake on obesity. The bootstrap CIs for Eggerthella, Butyricimonas, Coprococcus, Acidaminococcus, Allisonella, Dialister, and Veillonella are $(-0.069,0.035),\hspace{0.17em}(-0.059,0.061),\hspace{0.17em}(-0.066,0.046),\hspace{0.17em}(-0.023,0.157),\hspace{0.17em}(-0.018,0.216),\hspace{0.17em}(-0.068,0.022)$⁠, and $(-0.079,0.072)$⁠, respectively

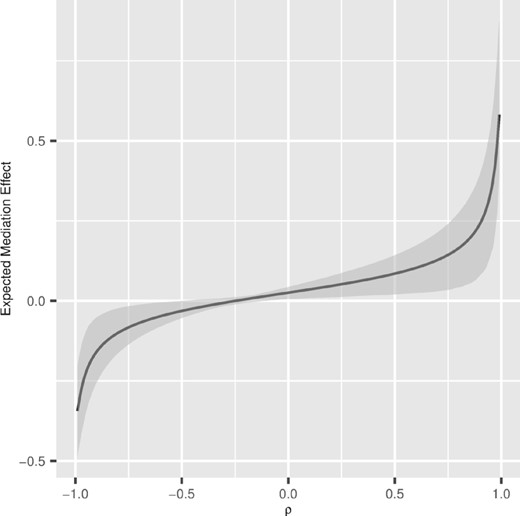
Since only Oscillibacter was identified as a potentially significant mediator, we included another genus to quantify the sensitivity of the assumption of the no unmeasured confounding effects. Note that CMM takes a compositional mediator so the number of components (mediators) must be greater than one. Figure 5 presents the result of the sensitivity analysis. The estimated mediation effect through Oscillibacter and Allisonella at ρ = 0 was 0.026 with a 95% bootstrap CI of (0.006, 0.043). For $-0.11\le \rho \le 1$⁠, the sign and significance of the estimated mediation effect remained unchanged. The 95% bootstrap CI covered the value of zero only when $-0.49\le \rho \le -0.12$⁠.

Fig. 5.

Sensitivity analysis. The dashed line indicates the estimated mediation effect for ρ = 0. The solid line represents the estimated mediation effect at each value of ρ, and the gray areas represent the 95% bootstrap CI for the mediation effects

4 Discussion

In this study, we propose a sparse compositional mediation model for binary outcomes. To account for the characteristics of compositional data, we adopt the staying-in-the-simplex approach to jointly estimate the effect of a treatment on all the components of a compositional mediator; and we use an L1-penalized log-contrast regression model to estimate the effects of treatment and the components of a compositional mediator on binary outcomes. We demonstrated that CMM performs better than the methods based on principal component approaches in simulation studies. CMM also provides which components (taxa) could be potential drivers of mediation effects, which cannot be obtained directly by the principal component-based approach. Applying CMM to the COMBO data, we found a significant positive mediation effect of the gut microbiome in linking fat intake and overweight/obesity.

CMM, like other causal mediation models, requires assumptions to identify the direct and indirect effects. These assumptions are generally not verifiable with observational data. However, the assumption that treatment assignment is ignorable given observed pretreatment covariates is usually attained in a subgroup having similar characteristics. The no-confounding effects assumption between mediators and an outcome is often taken for granted after the observed pretreatment covariates are adjusted, and its sensitivity to unmeasured confounding effects is often measured. We allow pretreatment covariates in modeling CMM and provide a method for sensitivity analysis.

For the rare outcome case, the natural direct and indirect effects can be defined in log odds ratios, assuming $U_{2i}$ follows a logistic distribution in Model (2); and their estimates can be approximated by c and ${(\text{log}\hspace{0.17em}\mathit{a})}^{\top }\mathit{b}$⁠, respectively. However, the logit model is computationally more intensive than the probit model for general cases in estimating the mediation effect. CMM was developed mainly for the general outcome case, which is more common in microbiome studies. So, CMM may not be an optimal method for the rare outcome. CMM uses a non-parametric bootstrap approach to testing the direct and indirect effects that involve the debiasing procedure, so it requires substantial computation time. For instance, it took 9 h and 29 min to run CMM with 100 samples and 200 components on a MacBook Pro with 2.0 GHz quad-core Intel Core i5. It would take longer if sensitivity analysis were also performed. We recommend sensitivity analysis be performed with a subset, as we did in the analysis of the COMBO data in Section 3.3.

The proposed method can be extended to multi-categorical treatments by utilizing indicator coding. However, extending CMM to multi-categorical outcomes or count outcomes is not trivial. These extensions are interesting future research topics. Another interesting and urgent extension of CMM is for longitudinal data, which has become increasingly common in clinical microbiome studies.

Acknowledgements

The authors would like to thank the reviewers for reviewing and suggesting valuable improvements to this work.

Funding

This work has been partially supported by the startup fund from the University of Rochester Medical Center.

Conflict of Interest: none declared.