Distribution-free tests of independence in high dimensions

Summary

We consider the testing of mutual independence among all entries in a |$d$|-dimensional random vector based on |$n$| independent observations. We study two families of distribution-free test statistics, which include Kendall’s tau and Spearman’s rho as important examples. We show that under the null hypothesis the test statistics of these two families converge weakly to Gumbel distributions, and we propose tests that control the Type I error in the high-dimensional setting where |$d >n$|⁠. We further show that the two tests are rate-optimal in terms of power against sparse alternatives and that they outperform competitors in simulations, especially when |$d$| is large.

1. Introduction

1.1. Literature review

Consider a |$d$|-dimensional continuous random vector |${X}$|⁠, where |${X}=(X_1,\ldots,X_d)^{{\mathrm{T}}}\in{{\mathbb{R}}}^d$|⁠. Given |$n$| samples, we aim to test the null hypothesis |$ {H_0:}$||$X_1,\ldots,X_d$| are mutually independent. This problem has been studied intensively in the case where |${X}$| is multivariate Gaussian. When |$d<n$|⁠, methods proposed include the likelihood ratio test (Anderson, 2003), Roy’s (1957) largest root test and Nagao’s (1973) test, which test the identity of the Pearson’s covariance matrix |${\Sigma}$| or the correlation matrix |${R}$| using their sample counterparts. When |$d$| and |$n$| both grow and the ratio |$d/n$| does not converge to zero, classic likelihood ratio tests perform poorly since the sample eigenvalues do not converge to their population counterparts (Bai & Yin, 1993). This has motivated work in high-dimensional settings.

In what follows, let |$\gamma$| denote the limit of |$d/n$| as |$n$| and |$d$| diverge to infinity. When |$0<\gamma\leq 1$|⁠, Bai et al. (2009) and Jiang & Yang (2013) proposed, and established the asymptotic normality of, corrected likelihood ratio test statistics. Specifically, Bai et al. (2009) considered the regime |$\gamma \in (0,1)$|⁠, and Jiang et al. (2012) extended it to the |$\gamma=1$| case. Johnstone (2001) and Bao et al. (2012) proved the Tracy–Widom law for the null limiting distributions of Roy’s largest root test statistics. The result of Bao et al. (2012) is only valid for |$\gamma\in(0,1)$|⁠, while the result of Johnstone (2001) applies to the case of |$\gamma=1$|⁠. These results are further generalized to |$\gamma>1$| in Péché (2009) and in Pillai & Yin (2012), with possibly non-Gaussian observations. When |$\gamma$| can be arbitrarily large but remains bounded, Ledoit & Wolf (2002) and Schott (2005) developed and established asymptotic normality of corrected Nagao test statistics. Jiang (2004) proposed a test statistic based on the largest sample correlation coefficient and showed that it converges to a Gumbel distribution, also known as an extreme-value Type I distribution. With some adjustments, Birke & Dette (2005) and Cai & Jiang (2012) proved that the tests of Ledoit & Wolf (2002) and Jiang (2004) extend to the case of |$\gamma=\infty$|⁠. To the best of our knowledge, there is no result generalizing the test of Schott (2005) to the regime |$\gamma=\infty$|⁠.

When |$\gamma$| can be infinity, Srivastava (2006) proposed a corrected likelihood ratio test using only nonzero sample eigenvalues. Srivastava (2005) introduced a test that uses unbiased estimators of the traces of powers of the covariance matrix. Cai & Ma (2013) showed that the test of Chen et al. (2010) uniformly dominates the corrected likelihood ratio tests of Bai et al. (2009) and Jiang & Yang (2013); the three test statistics are asymptotically normal. Zhou (2007) modified the test of Jiang (2004) and showed that the null limiting distribution of the test statistic is Gumbel.

Most of the aforementioned tests are valid only under normality. For non-Gaussian data, testing |$H_0$| in high dimensions is not as well studied: Péché (2009) and Pillai & Yin (2012) considered Roy’s largest root test for sub-Gaussian data; Bao et al. (2015) looked at the Spearman rho statistic; and Jiang (2004) examined the largest off-diagonal entry in the sample correlation matrix. In particular, Jiang (2004) showed that, for testing a simplified version of |$H_0$|⁠, the normality assumption can be relaxed to |${E}( |X|^{r})<\infty$| for some |$r>30$|⁠. Later, Zhou (2007) modified Jiang’s (2004) test to require only |$r\geq 6$|⁠. See also Li & Rosalsky (2006), Zhou (2007), Liu et al. (2008), Li et al. (2010), Cai & Jiang (2011, 2012), Shao & Zhou (2014) and Han et al. (2017).

This paper investigates testing |$H_0$| in high dimensions. The asymptotic regime of interest is where |$d$| and |$n$| both grow and |$d/n$| can diverge or converge to any nonnegative value. Our main focus is on nonparametric rank-based tests and their optimality. We consider two families of rank-based test statistics, which include Spearman’s rho (Spearman, 1904) and Kendall’s tau (Kendall, 1938), and prove that under the null hypothesis they converge weakly to Gumbel distributions. We also perform power analysis and establish optimality of the proposed tests against sparse alternatives, explicitly defined in § 4. In particular, we show that the tests based on Spearman’s rho and Kendall’s tau are rate-optimal against sparse alternatives.

1.2. Other related work

Testing |$H_0$| is related to testing bivariate independence. To test the independence between two random variables taking scalar values, Hotelling & Pabst (1936) and Kendall (1938) proposed using the Spearman’s rho and Kendall’s tau statistics, and Hoeffding (1948b) suggested the |$D$| statistic. To test the independence of two random vectors of possibly very high dimensions, Bakirov et al. (2006), Székely & Rizzo (2013) and Jiang et al. (2013) proposed tests based on normalized distance between characteristic functions, distance correlations and modified likelihood ratios. However, we cannot directly apply these results to test |$H_0$| without multiple testing adjustments.

A notable alternative to Pearson’s correlation coefficient is Spearman’s rho. Zhou (2007) established the limiting distribution of the largest off-diagonal entry of the Spearman’s rho correlation matrix, but did not provide a power analysis of the corresponding test. This paper includes the result of Zhou (2007) as a special case.

Many researchers have considered testing independence based on kernel methods (Gretton et al., 2007; Fukumizu et al., 2008; Póczos et al., 2012; Reddi & Póczos, 2013). They have focused on kernel dependence measures, the Hilbert–Schmidt norm of the cross-covariance operator (Gretton et al., 2007), or the normalized cross-covariance operator (Fukumizu et al., 2008). Using these dependence measures, early works concerned testing independence between two random variables (Gretton et al., 2007; Fukumizu et al., 2008) that might live in arbitrary sample spaces. Recently, Reddi & Póczos (2013) generalized the proposal in Fukumizu et al. (2008) and developed a copula-based kernel dependence measure for testing mutual independence. Póczos et al. (2012) offer an alternative kernel-based test using the maximum mean discrepancy (Borgwardt et al., 2006) between the empirical copula and the joint distribution of |$d$| independent uniform random variables. However, existing kernel-based tests were developed in the low-dimensional setting; Ramdas et al. (2015) have shown that such tests have low power in high dimensions.

During the preparation of this paper, it came to our attention that Mao (2017) and Leung & Drton (2017) also considered testing |$H_0$| for non-Gaussian data in high dimensions. These authors have proposed tests based on sums of rank correlations, such as Kendall’s tau (Leung & Drton, 2017) and Spearman’s rho (Mao, 2017; Leung & Drton, 2017). They further established asymptotic normality of the proposed test statistics in the case where |$\gamma$| can be arbitrarily large but is bounded. In particular, the theory in Mao (2017) follows from the procedure developed in Schott (2005), and the theory in Leung & Drton (2017) relies on |$U$|-statistics theory.

2. Testing procedures

2.1. Two families of tests

Let |$\{X_{i,\cdot}= (X_{i,1},\ldots, X_{i,d})^{{\mathrm{T}}},\, i=1,\ldots,n\}$| be |$n$| independent replicates of a |$d$|-dimensional random vector |${X}\in{\mathbb{R}}^d$|⁠. To avoid discussion of possible ties, we consider continuous random vectors. For any two entries |$j\ne k \in \{1,\ldots,d\}$|⁠, let |$Q_{ni}^{j}$| be the rank of |$X_{i,j}$| in |$\{X_{1,j},\ldots, X_{n,j}\}$| and let |$R_{ni}^{jk}$| be the relative rank of the |$k$|th entry compared to the |$j$|th entry; that is, |$R_{ni}^{jk} \equiv Q_{ni'}^k$| subject to the constraint that |$Q_{ni'}^j=i$| for |$i=1,\ldots,n$|⁠.

We propose two families of nonparametric tests based on the relative ranks. The first family includes tests based on simple linear rank statistics of the form

\begin{align}\label{eq:SLR} V_{jk}\equiv\sum_{i=1}^n c_{ni}g\{R_{ni}^{jk}/(n+1)\} \quad (j\ne k \in \{1,\ldots,d\}), \end{align}

(1)

where |$\{c_{ni}, \,i=1,\ldots,n\}$| form an array of constants called the regression constants and |$g(\cdot)$| is a Lipschitz function called the score function. We assume |$\sum_{i=1}^n c_{ni}^2>0$| to avoid triviality. It is immediately clear that Spearman’s rho belongs to the family of simple linear rank statistics. To accommodate tests of independence, we further pose the alignment assumption

\begin{align}\label{eq:alignment-assumption} c_{ni}=n^{-1} f\{i/(n+1)\}, \end{align}

(2)

where |$f(\cdot)$| is a Lipschitz function. Under this assumption, the simple linear rank statistic is a general measure of the agreement between the ranks of two sequences. It will be made clear in § § 3 and 4 that the alignment assumption (2) is not required in deriving the null limiting distribution, but is crucial in the power analysis.

The second family includes tests based on rank-type |$U$|-statistics, i.e., |$U$|-statistics of order |$m<n$| that depend only on the relative ranks |$\{R_{ni}^{jk}, \,i =1,\ldots, n\}$|⁠. In other words, a rank-type |$U$|-statistic takes the form

\begin{align} \label{eq:rankU} U_{jk}\equiv \frac{1}{n(n-1)\cdots(n-m+1)}\sum_{i_1\ne i_2\ne \cdots\ne i_m}\!\!h(X_{i_1,\{j,k\}},\ldots,X_{i_m,\{j,k\}}) (j\ne k \in \{1,\ldots,d\}), \end{align}

(3)

and |$U_{jk}$| depends only on |$\{R_{ni}^{jk}\}_{i=1}^n$|⁠. Here, for any vector |$X_{i,\cdot}$| and some index set |${\mathcal{A}}\subset\{1,\ldots,d\}$|⁠, let |$X_{i,{\mathcal{A}}}$| be the subvector of |$X_{i,\cdot}$| with entries in the index set |${\mathcal{A}}$|⁠. The kernel function |$h(\cdot)$| is assumed to be bounded but not necessarily symmetric. The boundedness assumption is mild since correlation is the object of interest.

Next, we propose two tests based on the two families of statistics. We begin with a testing procedure based on simple linear rank statistics. Under |$H_0$|⁠, the distribution of |$V_{jk}$| is irrelevant to the specific distribution of |${X}$| for all |$j\ne k \in \{1,\ldots,d\}$|⁠. Accordingly, the mean and variance of |$V_{jk}$| are calculable without knowing the true distribution. Let |${E}_{ H_0}(\cdot)$| and |${\rm var}_{H_0}(\cdot)$| be the expectation and variance of a certain statistic under |${ H_0}$|⁠. We have

\begin{align}\label{eq:mvinh0} {E}_{H_0} (V_{jk}) = \bar g_n \sum_{i=1}^n c_{ni},\quad {\rm var}_{H_0} (V_{jk})=\frac{1}{n-1}\sum_{i=1}^n \bigl[g\{i/(n+1)\}-\bar g_n\bigr]^2 \sum_{i=1}^n (c_{ni}-\bar c_n)^2, \end{align}

(4)

where |$\bar g_n \equiv n^{-1}\sum_{i=1}^n g\{i/(n+1)\}$| is the sample mean of |$g\{R_{ni}^{jk}/(n+1)\}$||$(i=1,\ldots,n)$|⁠. Based on |$\{V_{jk}, 1\leq j < k \leq d\}$|⁠, we propose the following statistic for testing |$H_0$|⁠:

\begin{align}\label{eq:Ln} L_n \equiv \max_{j < k}\: \bigl|V_{jk}-{E}_{ H_0} (V_{jk})\bigr|\text{.} \end{align}

(5)

As with simple linear rank statistics, the expectation and variance of the rank-type |$U$|-statistics |${E}_{H_0} (U_{jk})$| and |${{\rm var}}_{ H_0} (U_{jk})$| can be calculated analytically. We can test |$H_0$| using

\begin{align}\label{eq:tLn} \tilde L_n \equiv \max_{j < k} \:\bigl|U_{jk}-{E}_{H_0} (U_{jk})\bigr|\text{.} \end{align}

(6)

Detailed studies of the null limiting distributions of |$L_n$| and |$\tilde L_n$| are deferred to § 3. Here we give some intuition. Under certain conditions, the standardized version of |$V_{jk}$| or |$U_{jk}$| is asymptotically normal. Accordingly, the standardized version of |$L_n^2$| or |$\tilde L_n^2$| is asymptotically close to the maximum of |$d(d-1)/2$| independent chi-squared random variables with one degree of freedom. The latter converges weakly to a Gumbel distribution after adjustment.

Let |$\sigma_V^2$| and |$\sigma_U^2$| be the variances of |$n^{1/2}V_{jk}$| and |$n^{1/2} U_{jk}$| under |$H_0$|⁠, i.e.,

\begin{align}\label{eq:sigma} \sigma_V^2 \equiv n\,{{\rm var}}_{H_0} (V_{jk}), \quad \sigma_U^2 \equiv n\,{{\rm var}}_{ H_0} (U_{jk})\text{.} \end{align}

(7)

We propose the following size-|$\alpha$| tests |${T}_{\alpha}$| and |$\tilde{T}_{\alpha}$| of |$H_0$|⁠:

\begin{equation}\label{eq:qq-alpha} {T}_{\alpha}\equiv I\!\left( \frac{n L_n^2}{\sigma_V^{2}} - 4\log d+\log\log d \geq q_{\alpha} \right)\!,\quad \tilde{T}_{\alpha} \equiv I \!\left( \frac{n\tilde L_n^2}{\sigma_U^{2}}-4\log d+\log\log d \geq q_{\alpha}\right)\!\text{.} \end{equation}

(8)

Here |$I(\cdot)$| represents the indicator function and

\begin{align}\label{eq:q-alpha} q_{\alpha}\equiv-\log(8\pi) -2\log\log (1-\alpha)^{-1} \end{align}

(9)

is the |$1-\alpha$| quantile of the Gumbel distribution function |$\exp\{-(8\pi)^{-1/2}\exp(-y/2)\}$|⁠. In what follows, we consider a fixed nominal significance level, such as |$\alpha = 0{\cdot}05$|⁠.

Alternatively, we can simulate the exact distribution of the studied statistic and choose |$q_{\alpha}$| to be the |$1-\alpha$| quantile of the corresponding empirical distribution. This simulation-based approach is discussed in the Supplementary Material.

2.2. Examples

In this subsection, we present four distribution-free tests of independence that belong to the two general families defined in § 2.1.

 

Example 1

(Spearman’s rho). Recall that |$Q_{ni}^j$| and |$Q_{ni}^k$| are the ranks of |$X_{i,j}$| and |$X_{i,k}$| among |$\{X_{1,j},\ldots,X_{n,j}\}$| and |$\{X_{1,k},\ldots,X_{n,k}\}$|⁠, respectively. Spearman’s rho is defined as

\begin{align*} \rho_{jk} &= \frac{\sum_{i=1}^n (Q_{ni}^j-\bar Q_n^j)(Q_{ni}^k-\bar Q_n^k)}{ \bigl\{ \sum_{i=1}^n (Q_{ni}^j-\bar Q_n^j)^2 \sum_{i=1}^n (Q_{ni}^k-\bar Q_n^k)^2 \bigr\}^{1/2} } \notag \\ & =\frac{12}{n(n^2-1)}\sum_{i=1}^n \left(i-\frac{n+1}{2}\right)\!\left(R_{ni}^{jk}-\frac{n+1}{2}\right) \quad (j\ne k \in \{1,\ldots,d\}), \end{align*}

where |$\bar Q_n^j=\bar Q_n^k \equiv (n+1)/2$|⁠. This is a simple linear rank statistic, and we have

\[ {E}_{ H_0}(\rho_{jk})=0, \quad {{\rm var}}_{ H_0} (\rho_{jk}) = (n-1)^{-1} \quad (j\ne k \in \{1,\ldots,d\})\text{.} \]

According to (8), the corresponding test statistic is

\[ {T}^{\rho}_{\alpha} = I\!\left\{(n-1)\max_{j<k} \rho_{jk}^2 - 4\log d+\log\log d \geq q_{\alpha}\right\}\!\text{.} \]

 

Example 2

(Kendall’s tau). Kendall’s tau is defined, for |$j\ne k \in \{1,\ldots,d\}$|⁠, by

\[ \tau_{jk} = \frac{2}{n(n-1)} \sum_{i<i'} {\mathrm{sign}}(X_{i',j}-X_{i,j})\,{\mathrm{sign}}(X_{i',k}-X_{i,k})=\frac{2}{n(n-1)}\sum_{i<i'}{\mathrm{sign}}(R_{ni'}^{jk}-R_{ni}^{jk}), \]

where the sign function |${\mathrm{sign}}(\cdot)$| is defined as |${\mathrm{sign}}(x)= x/|x|$| with the convention |$0/0=0$|⁠. This statistic is a function of the relative ranks |$\{R_{ni}^{jk}, \,i=1,\ldots,n\}$| and is also a |$U$|-statistic with bounded kernel |$h(x_{1,\{1,2\}} ,x_{2,\{1,2\}})\equiv {\mathrm{sign}}(x_{1,1}-x_{2,1})\,{\mathrm{sign}}(x_{1,2}-x_{2,2})$|⁠. Accordingly, Kendall’s tau is a rank-type |$U$|-statistic. Moreover,

\[ {E}_{ H_0} (\tau_{jk})=0, \quad {{\rm var}}_{H_0} (\tau_{jk}) = \frac{2(2n+5)}{9n(n-1)} \quad (j\ne k \in \{1,\ldots,d\})\text{.} \]

According to (8), the proposed test statistic based on Kendall’s tau is

\[ {T}^{\tau}_{\alpha} = I\!\left\{\frac{9n(n-1)}{2(2n+5)}\max_{j<k} \tau_{jk}^2 - 4\log d+\log\log d \geq q_{\alpha}\right\}\text{.} \]

 

Example 3

(A major part of Spearman’s rho). Although Spearman’s rho is not a |$U$|-statistic, by Hoeffding (1948a) we can write, for |$j\ne k \in \{1,\ldots,d\}$|⁠,

\begin{align*} \rho_{jk}=\frac{n-2}{n+1} \,\hat\rho_{jk} + \frac{3\tau_{jk}}{n+1}, \end{align*}

where

\[ \hat\rho_{jk} = \frac{3}{n(n-1)(n-2)}\sum_{i \ne i' \ne i''} {\mathrm{sign}}(X_{i,j}-X_{i',j})\,{\mathrm{sign}}(X_{i,k}-X_{i'',k})\text{.} \]

Here |$\hat\rho_{jk}$| is a |$U$|-statistic of degree three with an asymmetric bounded kernel. Moreover,

\[ {E}_{ H_0}(\hat\rho_{jk})=0, \quad {{\rm var}}_{H_0} (\hat\rho_{jk})=\frac{n^2-3}{n(n-1)(n-2)} \quad (j\ne k \in \{1,\ldots,d\})\text{.} \]

As in (8), the test based on |$\{\hat\rho_{jk}, 1\leq j < k \leq d\}$| is

\[ {T}^{\hat\rho}_{\alpha} = I\!\left\{\frac{n(n-1)(n-2)}{n^2-3}\,\max_{j<k} \hat\rho_{jk}^2 - 4\log d+\log\log d \geq q_{\alpha}\right\}\text{.} \]

 

Example 4

(Projection of Kendall’s tau to simple linear rank statistics). Kendall’s tau does not belong to the family of simple linear rank statistics. However, by the projection argument in Hájek (1968), |$\tau_{jk}$| can be approximated by

\[ \hat\tau_{jk}= \frac{8}{n^2(n-1)}\sum_{i=1}^n \left(i-\frac{n+1}{2}\right)\!\left(R_{ni}^{jk}-\frac{n+1}{2}\right) \quad (j\ne k \in \{1,\ldots,d\})\text{.} \]

Using the variance of |$\rho_{jk}$| and the relationship between |$\rho_{jk}$| and |$\hat\tau_{jk}$|⁠, it is easy to obtain that

\[ {E}_{H_0} (\hat\tau_{jk})=0, \quad {{\rm var}}_{ H_0} (\hat\tau_{jk}) =\frac{4(n+1)^2}{9n^2(n-1)} \quad (\,j\ne k \in \{1,\ldots,d\})\text{.} \]

We observe that |${{\rm var}}_{ H_0}(\hat\tau_{jk})/{{\rm var}}_{ H_0}(\tau_{jk})$| goes to unity as |$n$| grows, indicating that |$\hat\tau_{jk}$| is asymptotically equivalent to |$\tau_{jk}$| under |${H_0}$|⁠. The proposed test statistic is

\[ {T}^{\hat{\tau}}_{\alpha} = I\!\left\{\frac{9n^2(n-1)}{4(n+1)^2}\max_{j<k} \hat\tau_{jk}^2 - 4\log d+\log\log d \geq q_{\alpha}\right\}\text{.} \]

 

Remark 1.

We have considered two families of test statistics: a family of simple linear rank statistics and a family of rank-type |$U$|-statistics. Waerden (1957) and Woodworth (1970) studied the performance of Spearman’s rho and Kendall’s tau in testing bivariate independence under normality, and showed that Spearman’s rho is more efficient than Kendall’s tau when |$n$| is small, while the reverse is true if |$n$| is large. Although the threshold point is theoretically calculable, in practice it is very difficult to approximate.

3. Limiting null distributions

In this section we characterize the limiting distributions of |$L_n$| and |$\tilde L_n$| under |$H_0$|⁠. We first introduce some necessary notation. Let |$v=(v_1,\ldots,v_d)^{{\mathrm{T}}}\in{\mathbb{R}}^d$| be a |$d$|-vector and let |${M}=[{M}_{jk}]\in {\mathbb{R}}^{d\times d}$| be a |$d \times d$| matrix. For index sets |$I,J\subset\{1,\ldots,d\}$|⁠, let |$v_I$| be the subvector of |$v$| with entries indexed by |$I$|⁠, and let |${M}_{I,J}$| be the submatrix of |${M}$| with rows indexed by |$I$| and columns indexed by |$J$|⁠. Let |$\lambda_{\min}({M})$| denote the smallest eigenvalue of |${M}$|⁠. For two sequences |$\{a_1,a_2,\ldots\}$| and |$\{b_1,b_2,\ldots\}$|⁠, we write |$a_n=O(b_n)$| if there exists some constant |$C$| such that for any sufficiently large |$n$|⁠, |$\:|a_n|\leq C|b_n|$|⁠. We write |$a_n=o(b_n)$| if for any positive constant |$c$| and any sufficiently large |$n$|⁠, |$\:|a_n| \leq c|b_n|$|⁠. We write |$a_n=o_y(b_n)$| if the constant depends on some scalar |$y$|⁠, i.e., |$|a_n| \leq c_y|b_n|$|⁠. We study the asymptotics of triangular arrays (Greenshtein & Ritov, 2004), allowing the dimension |$d \equiv d_n$| to grow with |$n$|⁠. In the following |$c$| and |$C$| will represent generic positive constants, whose values may vary at different locations.

We first consider the simple linear rank statistic |$V_{jk}$|⁠. The following theorem shows that under |$H_0$| and some regularity conditions on the regression constants |$\{c_{n1},\ldots,c_{nn}\}$|⁠, the statistic |$nL_n^2/\sigma_V^2-4\log d+\log\log d$| converges weakly to a Gumbel distribution.

 

Theorem 1.

Suppose that the simple linear rank statistics |$\{V_{jk}, \,1\leq j<k\leq d\}$| take the form (1) with regression constants |$\{c_{n1},\ldots,c_{nn}\}$| satisfying

\begin{align}\label{eq:cn} \max_{1\leq i \leq n} |c_{ni}-\bar c_n|^2 \leq \frac{C_1^2}{n} \sum_{i=1}^n (c_{ni}-\bar c_n)^2 , \quad \left|\sum_{i=1}^n (c_{ni}-\bar c_n)^3\right|^2 \leq \frac{C_2^2}{n}\left\{\sum_{i=1}^n (c_{ni}-\bar c_n)^2\right\}^{3}\!\!, \end{align}

(10)

where |$\bar c_n \equiv \sum_{i=1}^n c_{ni}$| represents the sample mean of the regression constants and |$C_1$| and |$C_2$| are two constants. Further suppose that the score function |$g(\cdot)$| is differentiable with bounded Lipschitz constant. Then under |$H_0$|⁠, if |$\log d=o(n^{1/3})$| as |$n$| grows, for any |$y\in{\mathbb{R}}$| we have

\[ \big|{\rm{pr}}(nL_n^2/\sigma^2_V-4\log d +\log\log d\leq y) - \exp\{-(8\pi)^{-1/2}\exp(-y/2) \}\big|=o_y(1), \]

where |$L_n$| and |$\sigma^2_V$| are defined in (5) and (7).

It is common to have conditions of the form (10) in Theorem 1 for the simple linear rank statistics to be asymptotically normal or to deviate moderately from normality; see Hájek et al. (1999) and Kallenberg (1982). Seoh et al. (1985) gave similar conditions for |$\{c_{ni}, \,i=1, \ldots, n\}$|⁠. The Lipschitz condition rules out the Fisher–Yates statistic, where |$g(\cdot)$| is proportional to |$\Phi^{-1}\{\cdot/(n+1)\}$| and |$\Phi^{-1}(\cdot)$| represents the quantile function of the standard Gaussian.

Theorem 1 gives a distribution-free result for testing |$H_0$| (see Kendall & Stuart, 1961, Ch. 31). In contrast, tests based on sample covariance and correlation matrices (e.g., Jiang, 2004; Li et al., 2010; Cai & Jiang, 2011; Shao & Zhou, 2014) are not distribution-free; for instance, Li et al. (2010) and Shao & Zhou (2014) impose moment requirements on |${X}$|⁠.

Spearman’s rho is a simple linear rank statistic, and it satisfies the conditions (10). Therefore, Theorem 1 is a strict generalization of Theorem 1.2 in Zhou (2007).

We now turn to rank-type |$U$|-statistics. The next theorem is the analogue of Theorem 1.

 

Theorem 2.

Suppose that the rank-type |$U$|-statistics |$\{U_{jk}, \, 1\leq j<k\leq d\}$| are of the form (3) and of degree |$m$|⁠, and that the kernel function |$h(\cdot)$| is bounded and nondegenerate. Then under |$H_0$|⁠, if |$\log d=o(n^{1/3})$| as |$n$| grows, for any |$y\in{\mathbb{R}}$| we have

\[ \big|{\rm{pr}}(n\tilde L_n^2/\sigma^2_U-4\log d +\log\log d\leq y) - \exp\{-(8\pi)^{-1/2}\exp(-y/2) \}\big|=o_y(1), \]

where |$\tilde L_n$| and |$\sigma^2_U$| are defined in (6) and (7).

The assumption on |$h(\cdot)$| requires that the rank-type |$U$|-statistic be nondegenerate; hence it rules out Hoeffding’s |$D$| statistic.

Corollary 1 says that the tests |${T}_{\alpha}$| and |$\tilde{T}_{\alpha}$| can effectively control the size.

 

Corollary 1.

Suppose that the conditions in Theorem 1 or Theorem 2 hold; then, respectively, |${\rm{pr}}({T}_{\alpha}=1 \mid { H_0}) = \alpha + o(1), \quad {\rm{pr}}(\tilde{T}_{\alpha}=1 \mid { H_0}) = \alpha + o(1)\text{.}$| Furthermore, all test statistics in Examples 1–4 converge weakly to a Gumbel distribution.

 

Corollary 2.

Under the regime where |$\log d=o(n^{1/3})$| as |$n$| grows, |${\rm{pr}}({T}_{\alpha}^{\ell}=1 \mid { H_0}) = \alpha + o(1) \quad (\ell \in\{\rho,\tau,\hat\rho,\hat\tau\}),$| where |${T}_{\alpha}^{\ell}$| corresponds to the test statistics introduced in Examples 1–4 for |$\ell \in\{\rho,\tau,\hat\rho,\hat\tau\}$|⁠.

4. Power analysis and optimality properties

4.1. Sparse alternatives

Let |${\mathcal{U}}(c)$| be a set of matrices indexed by a constant |$c$|⁠,

\begin{align}\label{eq:matrix-set} {\mathcal{U}}(c)\equiv\left\{ {M}\in{\mathbb{R}}^{d\times d}: {\mathrm{diag}}({M})={I}_d, \: {M}={M}^{{\mathrm{T}}}, \:\max_{1\leq j<k\leq d} |{M}_{jk}| \geq c (\log d/n)^{1/2} \right\}, \end{align}

(11)

where |${I}_d$| denotes the |$d \times d$| identity matrix and |${\mathrm{diag}}({M})$| represents a matrix with diagonal elements equal to the diagonal elements of |${M}$| and with all off-diagonal elements equal to zero.

We define the random matrix |$\hat{V}=[\hat{V}_{jk}]\in{\mathbb{R}}^{d\times d}$| by

\[ \hat{V}_{jk}=\hat{V}_{kj}=\sigma_V^{-1} \{ V_{jk}-{E}_{ H_0} (V_{jk})\}, \quad \hat{V}_{\ell \ell}=1 \quad (1\leq j<k\leq d;\, 1\leq \ell \leq d), \]

where |$\sigma_V$| is defined in (7) and |$\{V_{jk},\, 1\leq j<k\leq d\}$| are the simple linear rank statistics. Let the population version of |$\hat{V}$| be |$V\equiv{E}(\hat{V})$|⁠. We study the power of tests against the alternative

\begin{equation}\label{eq:alternative_SLR} { H_{\rm a}^{V}}(c) \equiv \{F({X}): V\{F({X})\} \in {\mathcal{U}}(c) \}, \end{equation}

(12)

where |$F(X)$| is the joint distribution function of |${X}$| and we write |$V\{F({X})\}$| to emphasize that |$V=E(\hat V)=\int \hat V \,\mathrm{d} F({X})$| is a function of |$F({X})$|⁠.

Similarly, we define the random matrix |$\hat{U}=[\hat{U}_{jk}] \in {\mathbb{R}}^{d\times d}$| by

\[ \hat{U}_{jk}=\hat{U}_{kj}=\frac{U_{jk}-{E}_{ H_0} (U_{jk})}{\tilde\sigma_U}, \quad \hat{U}_{\ell \ell}=1 \quad (1\leq j<k\leq d; \, 1\leq \ell \leq d), \]

where |$\{U_{jk}, \,1\leq j<k\leq d\}$| are the rank-type |$U$|-statistics and

\begin{equation}\label{eqn:sigma_tilde} \tilde\sigma_U^2\equiv m^2 \,{\rm var}_{ H_0} \bigl[{E}_{ H_0}\{h(X_{1,\{1,2\}},\ldots,X_{m,\{1,2\}})\mid X_{1,\{1,2\}}\}\bigr]\text{.} \end{equation}

(13)

We define the population version of |$\hat{U}$| to be |${U}\equiv{E}(\hat{U})$|⁠. Then we study the power of tests against the alternative

\begin{equation}\label{eq:alternative_rankU} { H_{\rm a}^{U}}(c) \equiv \{F({X}): {U}\{F({X})\} \in {\mathcal{U}}(c) \}\text{.} \end{equation}

(14)

When studying rate-optimality, we consider the alternative

\begin{equation}\label{eq:alternative_R} { H_{\rm a}^{R}}(c) \equiv \{F({X}): {R}\{F({X})\} \in {\mathcal{U}}(c) \}, \end{equation}

(15)

where |${R}$| is the population correlation matrix; § 4.3 clarifies why we use |${ H_{\rm a}^{R}}(c)$| in (15).

All three alternatives are based on the set of matrices |${\mathcal{U}}(c)$|⁠, of which at least one entry has magnitude greater than |$C(\log d/n)^{1/2}$| for some large constant |$C$|⁠; so we call (12), (14) and (15) the sparse alternatives.

The three alternatives may not be equivalent. For instance, |$\max_{1\leq j<k\leq d} |V_{jk}| \geq c (\log d/n)^{1/2}$| does not imply |$\max_{1\leq j<k\leq d} |{U}_{jk}| \geq c (\log d/n)^{1/2}$|⁠. The exact relationship between |${ H_{\rm a}^{V}}$| and |${ H_{\rm a}^{U}}$| is intriguing. Taking Kendall’s tau and Spearman’s rho as examples, Fredricks & Nelsen (2007) have shown that for a bivariate random vector, the ratio between the population analogues of the two statistics converges to |$3/2$| as the joint distribution approaches independence. Under a fixed alternative, however, the relationship between the population analogues of Kendall’s tau and Spearman’s rho remains unclear and probably depends heavily on the specific distribution. Hence, we do not pursue a theoretical comparison of the powers of the tests.

4.2. Power analysis

The following theorem characterizes the conditions under which the power of |${T}_{\alpha}$| tends to unity as |$n$| grows, under the alternative |${ H_{\rm a}^{V}}$| in (12).

 

Theorem 3.

Assume that the alignment assumption in (2) holds, and that |$\sigma_V^2 = A_1\{1+o(1)\}$| and |$\max\{|f(0)|,|g(0)|\}\leq A_2$| for some positive constants |$A_1$| and |$A_2$|⁠. Further assume that |$f(\cdot)$| and |$g(\cdot)$| have bounded Lipschitz constants. Then, for some large scalar |$B_1$| depending only on |$A_1$|⁠, |$A_2$| and the Lipschitz constants of |$f(\cdot)$| and |$g(\cdot)$|⁠,

\[ \inf_{F({X}) \in {H_{\rm a}^{V}}(B_1)} {\rm{pr}}({T}_{\alpha}=1) =1 - o(1), \]

where the infimum is taken over all distributions |$F({X})$| such that |$V \{F({X})\}\in{\mathcal{U}}(B_1)$|⁠.

Similarly, |$\tilde{T}_{\alpha}$| has the property of the power tending to unity under the alternative |$H_{\rm a}^{U}$| in (14).

 

Theorem 4.

Suppose that the kernel function |$h(\cdot)$| in (3) is bounded with |$|h(\cdot)|\leq A_3$| and

\[ m^2 \,{\rm var}_{ H_0}\bigl[ {E}_{ H_0}\{h(X_{1,\{1,2\}},\ldots,X_{m,\{1,2\}}) \mid X_{1,\{1,2\}} \} \bigr]= \{1+o(1)\}A_4 \]

for some positive constants |$A_3$| and |$A_4$|⁠. Then, for some large scalar |$B_2$| depending only on |$A_3$|⁠, |$A_4$| and |$m$|⁠,

\[ \inf_{F({X}) \in {H_{\rm a}^{U}}(B_2)} {\rm{pr}}(\tilde{T}_{\alpha}=1) =1 - o(1), \]

where the infimum is taken over all distributions |$F({X})$| such that |${U}\{F({X})\} \in{\mathcal{U}}(B_2)$|⁠.

Here |$H_{\rm a}^{V}(B_1)$| and |$H_{\rm a}^{U}(B_2)$| are both sparse alternatives, which can be very close to the null in the sense that all but a small number of entries in |$V$| or |${U}$| can be exactly zero. The above theorems show that the proposed tests are sensitive to small perturbations to the null. For the examples discussed in § 2, Theorems 3 and 4 show that their powers tend to unity under the sparse alternative.

4.3. Optimality

We now establish the optimality of the proposed tests in the following sense. Recall that |${T}_{\alpha}$| and |$\tilde{T}_{\alpha}$| can correctly reject the null hypothesis provided that at least one entry of |$V$| or |${U}$| has magnitude greater than |$C(\log d/n)^{1/2}$| for some constant |$C$|⁠. We show that such a bound is {rate-optimal}, i.e., that the rate of the signal gap, |$(\log d/n)^{1/2}$|⁠, cannot be relaxed further.

For each |$n$|⁠, define |${\mathcal{T}}_{\alpha}$| to be the set of all measurable size-|$\alpha$| tests. In other words, |${\mathcal{T}}_{\alpha}\equiv\{T_{\alpha}: {\rm{pr}}(T_{\alpha}=1 \mid { H_0})\leq \alpha\}$|⁠.

 

Theorem 5.

Assume that |$c_0< 1$| is a positive constant, and let |$\beta$| be a positive constant satisfying |$\alpha+\beta<1$|⁠. Under the regime where |$\log d/n=o(1)$| as |$n$| grows, for large |$n$| and |$d$| we have

\[ \inf_{T_{\alpha}\in {\mathcal{T}}_{\alpha}}\:\sup_{F({X}) \in { H_{\rm a}^{R} }(c_0) }{\rm{pr}}(T_{\alpha}=0) \geq 1-\alpha-\beta, \]

where the supremum is taken over the distribution family |$ { H_{\rm a}^{R}(c_0) }$| defined in (15).

Theorem 5 shows that any measurable size-|$\alpha$| test cannot differentiate between the null hypothesis |${H_0}$| and the sparse alternative when |$\max_{j<k}|{R}_{jk}| \leq c_0 (\log d/n)^{1/2}$| for some constant |$c_0<1$|⁠.

In the Supplementary Material we give the detailed proof of Theorem 5. It begins with the observation that the family of alternative distributions |$H_{\rm a}^{R}(c_0)$| includes some Gaussian distributions as a subset, since one can construct a Gaussian distribution given any |${R} \in {\mathcal{U}}(c_0)$|⁠. Therefore, the supremum over |${ H_{\rm a}^{R}(c_0)}$| is no smaller than the supremum over the Gaussian subset. The rest of the proof follows from the general framework in Baraud (2002). In particular, the proof technique is relevant to the argument used in deriving the lower bound in two-sample covariance tests (Cai et al., 2013).

Due to technical constraints, the alternative considered in Theorem 5 is defined with the Pearson’s population correlation matrix |${R}$|⁠. As mentioned in § 4.1, it is unclear whether there exist equivalences between |$V$|⁠, |${U}$| and |${R}$|⁠. Therefore, in order to apply Theorem 5 to the alternatives used in Theorems 3 and 4, we make the following assumptions.

 

Assumption 1.

When |${X}$| is Gaussian, the matrices |$V$| and |${R}$| are such that for large |$n$| and |$d$|⁠, |$\:cV_{jk} \leq {R}_{jk}\leq C V_{jk}$| for |$j\ne k \in \{1,\ldots,d\}$|⁠, where |$c$| and |$C$| are two constants.

 

Assumption 2.

When |${X}$| is Gaussian, the matrices |${U}$| and |${R}$| are such that for large |$n$| and |$d$|⁠, |$c{U}_{jk} \leq {R}_{jk}\leq C{U}_{jk}$| for |$j\ne k \in \{1,\ldots,d\}$|⁠, where |$c$| and |$C$| are two constants.

In the proof of Theorem 5, we obtain a lower bound by considering the Gaussian subset of |${H_{\rm a}^{R}}(c_0)$|⁠. This is why we require Assumptions 1 and 2 to hold at least for the Gaussian distributions. Theorem 5 then justifies the rate-optimality of the proposed tests, summarized as follows.

 

Theorem 6.

• (a) Suppose that the simple linear rank statistics |$\{V_{jk},\, 1\leq j<k\leq d\}$| satisfy all the conditions in Theorems 1 and 3. Suppose also that Assumption 1 holds. Then, under the regime where |$\log d=o(n^{1/3})$| as |$n$| grows, the corresponding size-|$\alpha$| test |${T}_{\alpha}$| is rate-optimal. In other words, there exist two constants |$D_1<D_2$| such that:

  • (i) |$\sup_{F({X}) \in { H_{\rm a}^{V}}(D_2)}{\rm{pr}}({T}_{\alpha}=0) = o(1);$|

  • (ii) for any |$\beta>0$| satisfying |$\alpha+\beta<1$|⁠, for large |$n$| and |$d$| we have

    \[ \inf_{T_{\alpha}\in {\mathcal{T}}_{\alpha}}\sup_{F({X}) \in { H_{\rm a}^{V}}(D_1)} {\rm{pr}}(T_{\alpha}=0)\geq 1-\alpha-\beta\text{.} \]

• (b) For all rank-type |$U$|-statistics satisfying the conditions in Theorems 2 and 4, if Assumption 2 holds, then the same rate-optimality property holds.

As an example, the next corollary justifies the test statistics in Examples 1–4.

 

Corollary 3.

The four test statistics in Examples 1–4 are all rate-optimal against the corresponding sparse alternatives.

Corollary 3 is a direct consequence of Theorem 6 and Lemma C8 in the Supplementary Material. Its proof is therefore omitted.

5. Numerical experiments

5.1. Tests

We compare the performances of our proposed tests and several competitors on various synthetic datasets in both low-dimensional and high-dimensional settings. Additional numerical results are reported in the Supplementary Material, which includes comparisons with other tests of |$H_0$|⁠, testings with simulation-based rejection thresholds, and an application.

We propose a test based on Spearman’s rho statistic, outlined in Example 1, using the result in Theorem 1. We also propose a test based on Kendall’s tau statistic, outlined in Example 2, using the result in Theorem 2. We use the theoretical rejection threshold |$q_{\alpha}$| in (9) for both tests. Below we will refer to these tests as the Spearman test and the Kendall test.

As a competitor, we consider the test of Zhou (2007), which rejects the null hypothesis if

\begin{align*} n\max_{j<k}r_{jk}^2-4\log d+\log\log d \geq q_{\alpha}, \end{align*}

where |$q_{\alpha}$| is the theoretical threshold defined in (9).

Another competitor is the test of Mao (2014), which rejects the null hypothesis if

\begin{align*} \left\{ \sum_{j<k} \frac{r_{jk}^2}{1-r_{jk}^2}-\frac{d(d-1)}{2(n-4)}\right\} \left\{ \frac{(n-4)^2(n-6)}{d(d-1)(n-3)} \right\}^{1/2} \geq \Phi^{-1}(1-\alpha ), \end{align*}

where |$\Phi^{-1}(\cdot)$| is the quantile function of the standard Gaussian. The test statistic in Mao (2014) has guaranteed size control only under normality.

A further two competitors are the kernel-based tests of Reddi & Póczos (2013) and Póczos et al. (2012). Briefly, Reddi & Póczos (2013) propose to calculate the Hilbert–Schmidt norm of the normalized cross-covariance operators after a copula transformation, and Póczos et al. (2012) propose using the estimated maximum mean discrepancy after a copula transformation. In both kernel-based tests, we use the Gaussian kernel with standard deviation being the median distance heuristic as in Reddi & Póczos (2013) and Póczos et al. (2012). We use simulation to determine the rejection thresholds for both tests, since the null distribution of |$F({X})$| is uniform. Although a theoretical rejection threshold is proposed in Póczos et al. (2012), it becomes too conservative in high dimensions.

In total, we apply six tests in the numerical experiments, namely the Spearman test outlined in Example 1, the Kendall test outlined in Example 2, and the tests of Zhou (2007), Mao (2014), Reddi & Póczos (2013) and Póczos et al. (2012). In the following experiments, we set the nominal significance level to |$\alpha=0{\cdot}05$| for all tests.

We also compared the performance of our procedures with that of two more rank-based statistics proposed by Mao (2017) and Leung & Drton (2017). Due to space limitations, these additional results are presented in the Supplementary Material.

5.2. Synthetic data analysis

We now perform size and power comparisons between the competing tests described in § 5.1. In this simulation, we generate synthetic data from five different types of distribution: the Gaussian distribution, the light-tailed Gaussian copula, the heavy-tailed Gaussian copula, the multivariate |$t$| distribution, and the multivariate exponential distribution. To evaluate the sizes of the tests, we generate data from the five types of distribution under the null, where all entries in |${X}$| are mutually independent. For evaluating the powers of the tests, we generate different sets of data from the five types of distribution under sparse alternatives. For instance, for the Gaussian distribution, we draw our data from |$N_d(0,{I}_d)$| to evaluate the size, and generate data from |$N_d(0,{R}^*)$| to evaluate the power. Here |${R}^* \in \mathbb{R}^{d \times d}$| is a positive-definite matrix whose off-diagonal entries are all zero except for eight randomly chosen entries. Details of the data-generating mechanism are given in the Supplementary Material.

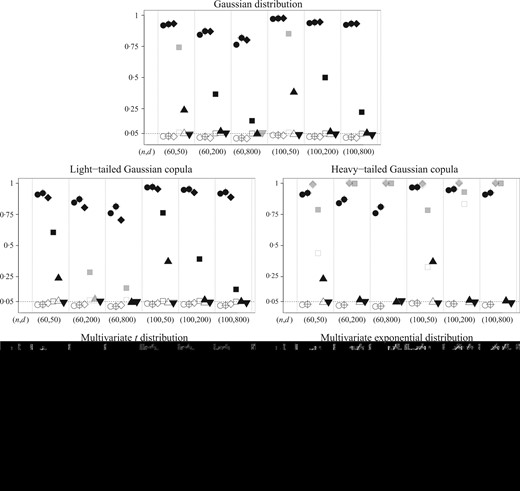
In summary, we generate data from ten distributions: one set under the null and one set under the sparse alternative for each of the five types of distribution. For each distribution, we draw |$n$| independent replicates of the |$d$|-dimensional random vector |${X} \in {\mathbb{R}}^d$|⁠. To examine the effects of increasing the sample size and dimension, we take the sample size |$n$| to be 60 or 100 and the dimension |$d$| to be 50, 200 or 800. Results from 5000 simulated datasets are shown in Fig. 1.

Fig. 1.

Empirical sizes and powers of six tests under five types of distribution averaged over 5000 replicates at the |$0{\cdot}05$| nominal significance level, shown by the horizontal dotted line in each panel. The vertical axis represents the proportion of rejected tests in the 5000 replicates. The vertical dotted lines separate six different data-generating schemes, for which |$(n,d)$| ranges from |$(60,50)$| to |$(100, 800)$|⁠. Only the pairs |$(60, 50)$| and |$(100,50)$| are in the low-dimensional setting. The six tests considered in the simulation are represented by: |$\circ$| and |$\bullet$|⁠, the Spearman test; |$\circ\!\!\!\!+$| and |$\bullet\!\!\!\!+$|⁠, the Kendall test; |$\diamond$| and |$\blacklozenge$|⁠, the test of Zhou (2007); |$\square$| and |$\blacksquare$|⁠, the test of Mao (2014); |$\delta$| and |$\blacktriangle$|⁠, the test of Reddi & Póczos (2013); |$\nabla$| and |$\blacktriangledown$|⁠, the test of Póczos et al. (2012). Hollow shapes, e.g., |$\circ\!\!\!\!+$|⁠, represent empirical sizes under the null, and solid shapes, e.g., |$\bullet\!\!\!\!+$|⁠, represent empirical powers under the alternative. A grey symbol, e.g., |$\delta$| and |$\delta$|⁠, indicates that the corresponding test fails to control the size at the |$0{\cdot}05$| nominal significance level in the corresponding null model. In this simulation, we say that a test fails to control the size at |$0{\cdot}05$| if its empirical size exceeds |$0{\cdot}05 + 1{\cdot}96(0{\cdot}05\times 0{\cdot}95/5000)^{1/2}$|⁠.

Under the Gaussian distribution, most tests can effectively control the size under all combinations of |$n$| and |$d$|⁠. Our proposed method and that of Zhou (2007) attain higher power than the other competitors. In contrast, the test of Mao (2014) has relatively low power; this is as expected because, under the sparse alternative, the correlation matrix has only eight nonzero entries. By averaging over all entries in the correlation matrix, the test of Mao (2014) is less sensitive to the sparse alternative. For similar reasons, the test of Póczos et al. (2012) has low power against the sparse alternative. The test of Reddi & Póczos (2013) has decreasing power as |$d$| grows, which corroborates the findings of Ramdas et al. (2015).

Under the light-tailed Gaussian copula, the performances of all six tests are similar to their performances under the Gaussian distribution. Notably, our proposed tests achieve higher power than the test of Zhou (2007), especially when the ratio |$d/n$| is large.

Under the heavy-tailed Gaussian copula, only our proposed tests correctly control the size while attaining high power. The tests of Zhou (2007) and Mao (2014) have very high power under the alternative, but their sizes are severely inflated under the null. The kernel-based tests of Reddi & Póczos (2013) and Póczos et al. (2012) correctly control the size but have very low power.

Under the multivariate |$t$| distribution, the performances are similar to those under the heavy-tailed Gaussian copula.

Under the multivariate exponential distribution, our proposed tests and the test of Reddi & Póczos (2013) achieve high power while correctly controlling the size across all settings. The tests of Mao (2014) and Zhou (2007) fail to control the size in high dimensions. The test of Póczos et al. (2012) has low power compared with the others.

In summary, our proposed tests correctly control the size and achieve high power across all types of distributions regardless of the sample size and dimension. The Kendall test performs slightly better than the Spearman test in terms of power. This is consistent with the observations in Woodworth (1970), which show that Kendall’s tau is asymptotically more powerful than Spearman’s rho in testing independence in terms of having the Bahadur efficiency bounded within |$(1,1{\cdot}05]$| under the Gaussian distribution. For the relationship between Spearman’s rho and Kendall’s tau under different alternatives, we refer to Fredricks & Nelsen (2007) for details. The performances of the tests of Zhou (2007) and Mao (2014) are strongly influenced by the data structure, and these tests cannot effectively control the size under heavy-tailed distributions. This is as expected because the validity of Mao’s (2014) test relies heavily on the Gaussian assumption, and the performance of Zhou’s (2007) test is related to the moments. The kernel-based tests of Reddi & Póczos (2013) and Póczos et al. (2012) control the size correctly in most cases, but their power suffers in high dimensions, as observed by Ramdas et al. (2015).

6. Discussion

The regression constants |$\{c_{ni}\}_{i=1}^n$|⁠, the score function |$g(\cdot)$| in (1), and the kernel function |$h(\cdot)$| in (3) are assumed to be identical across different pairs of entries; this condition can be straightforwardly relaxed, but for clarity of presentation we do not give further details in this direction.

The problem studied in this paper is related to one-sample and two-sample tests of equality of covariance or correlation matrices and to sphericity tests in high dimensions. There exist extensive studies along these lines of research; see, among others, Ledoit & Wolf (2002), Chen et al. (2010), Fisher et al. (2010), Srivastava & Yanagihara (2010), Fisher (2012), Li & Chen (2012), Cai et al. (2013), Zhang et al. (2013) and Han et al. (2017). For equity and sphericity tests, existing methods mostly focus on Pearson’s sample covariance matrix. Corresponding tests are based on statistics characterizing the difference between two-sample covariance matrices under different norms, such as the Frobenius norm or the maximum norm. As an alternative, Zou et al. (2014) proposed a sphericity test using the multivariate signs; however, the theoretical results in their paper are valid only under the regime where |$d=O(n^2)$|⁠.

Testing equality of covariance or correlation matrices is challenging since the random variables are not mutually independent. In the Supplementary Material, focusing on the one-sample test, we test the bandedness of the latent correlation matrix under the semiparametric Gaussian copula model. We show that the test built on Kendall’s tau statistic can asymptotically control the size and is rate-optimal against the sparse alternative. See the Supplementary Material for details.

Acknowledgement

We thank Cheng Zhou and Brian Caffo for helpful discussions, as well as the editor, associate editor and two referees for valuable suggestions. This research was supported in part by the U.S. National Science Foundation and National Institutes of Health.

Supplementary material

Supplementary material available at Biometrika online includes discussion of simulation-based rejection thresholds, generalizations of the proposed tests to other structural testing problems, additional numerical results, and proofs of the theoretical results.