Jeffreys-prior penalty, finiteness and shrinkage in binomial-response generalized linear models

Summary

Penalization of the likelihood by Jeffreys’ invariant prior, or a positive power thereof, is shown to produce finite-valued maximum penalized likelihood estimates in a broad class of binomial generalized linear models. The class of models includes logistic regression, where the Jeffreys-prior penalty is known additionally to reduce the asymptotic bias of the maximum likelihood estimator, and models with other commonly used link functions, such as probit and log-log. Shrinkage towards equiprobability across observations, relative to the maximum likelihood estimator, is established theoretically and studied through illustrative examples. Some implications of finiteness and shrinkage for inference are discussed, particularly when inference is based on Wald-type procedures. A widely applicable procedure is developed for computation of maximum penalized likelihood estimates, by using repeated maximum likelihood fits with iteratively adjusted binomial responses and totals. These theoretical results and methods underpin the increasingly widespread use of reduced-bias and similarly penalized binomial regression models in many applied fields.

1. Introduction

Logistic regression is one of the most frequently applied generalized linear models in statistical practice, both for inference about covariate effects on binomial probabilities and for prediction. Consider realizations |$y_1, \ldots, y_n$| of independent binomial random variables |$Y_1, \ldots, Y_n$| with success probabilities |$\pi_1, \ldots, \pi_n$| and totals |$m_1, \ldots, m_n$|⁠, respectively. Suppose that each |$y_i$| is accompanied by a |$p$|-dimensional covariate vector |$x_i$| and that the model matrix |$X$| with rows |$x_1, \ldots, x_n$| is of full rank. A logistic regression model has

$$\begin{equation} \label{binomialGLM} \pi_i = (G \circ \eta_i)(\beta), \quad \quad G(\eta) = \frac{\exp(\eta)}{1 + \exp(\eta)}, \quad \eta_i(\beta) = \sum_{t = 1}^p \beta_tx_{it} \quad (i = 1, \ldots, n), \end{equation}$$

(1)

where |$\beta = (\beta_1, \ldots, \beta_p)^{{ \mathrm{\scriptscriptstyle T} }}$| is the |$p$|-dimensional parameter vector and |$x_{it}$| is the |$t$|th element of |$x_i$|  |$(i = 1, \ldots, n)$|⁠; if an intercept parameter is present in the model, then the first column of |$X$| is a vector of ones. The maximum likelihood estimator |$\hat\beta$| of |$\beta$| in (1) maximizes the loglikelihood

$$\begin{equation} \label{loglik} l(\beta) = \sum_{i = 1}^n y_i \eta_i(\beta) - \sum_{i = 1}^n m_i \log\bigl[1 + \exp\{\eta_i(\beta)\}\bigr] . \end{equation}$$

(2)

Albert & Anderson (1984) categorized the possible settings for the sample points |$(y_1, x_1^{{ \mathrm{\scriptscriptstyle T} }})^{{ \mathrm{\scriptscriptstyle T} }}, \ldots, (y_n, x_n^{{ \mathrm{\scriptscriptstyle T} }})^{{ \mathrm{\scriptscriptstyle T} }}$| into complete separation, quasi-complete separation and overlap. Specifically, if there exists a vector |$\gamma \in \mathbb{R}^p$| such that |$\gamma^{{ \mathrm{\scriptscriptstyle T} }} x_i > 0$| for all |$i$| with |$y_i > 0$| and |$\gamma^{{ \mathrm{\scriptscriptstyle T} }} x_i < 0$| for all |$i$| with |$y_i = 0$|⁠, then there is complete separation in the sample points; if there exists a vector |$\gamma \in \mathbb{R}^p$| such that |$\gamma^{{ \mathrm{\scriptscriptstyle T} }} x_i \ge 0$| for all |$i$| with |$y_i > 0$| and |$\gamma^{{ \mathrm{\scriptscriptstyle T} }} x_i \le 0$| for all |$i$| with |$y_i = 0$|⁠, then there is quasi-complete separation in the sample points; and if the sample points exhibit neither complete separation nor quasi-complete separation, then they are said to overlap. Albert & Anderson (1984) showed that separation is necessary and sufficient for the maximum likelihood estimate to have at least one infinite-valued component. A parallel result appears in Silvapulle (1981), where it is shown that if |$G(\eta)$| in (1) is any strictly increasing distribution function such that |$-\!\log G(\eta)$| and |$\log\{1- G(\eta)\}$| are convex and if |$x_{i1} = 1$| for all |$i \in \{1, \ldots, n\}$|⁠, then the maximum likelihood estimate has all components finite if and only if there is overlap.

When data separation occurs, standard maximum likelihood estimation procedures, such as iteratively reweighted least squares (Green, 1984), can be numerically unstable due to the occurrence of large parameter values as the procedures attempt to maximize (2). In addition, inferential procedures that directly depend on the estimates and the estimated standard errors, such as Wald tests, can give misleading results. For a recent review of such problems and some solutions, see Mansournia et al. (2018).

Firth (1993) showed that if the logistic regression likelihood is penalized by Jeffreys’ invariant prior, then the resulting maximum penalized likelihood estimator has bias of smaller asymptotic order than that of the maximum likelihood estimator in general. Specifically, for logistic regressions the reduced-bias estimator |$\tilde\beta$| results from maximization of

$$\begin{equation} \label{penloglik} \tilde{l}(\beta) = l(\beta) + \frac{1}{2}\log\bigl|X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)X\bigr| \end{equation}$$

(3)

with |$W(\beta) = \mathop{\rm diag}\{w_1(\beta), \ldots, w_n(\beta)\}$|⁠, where |$w_i(\beta) = m_i(\omega \circ \eta_i)(\beta)$|  |$(i = 1, \ldots, n)$| is the working weight for the |$i$|th observation with |$\omega(\eta) = \exp(\eta)/\{1 + \exp(\eta)\}^2$|⁠. Heinze & Schemper (2002), in extensive numerical studies, observed that the reduced-bias estimates have finite values even when data separation occurs. Based on an argument about parameter-dependent adjustments to |$y_1, \ldots, y_n$| and |$m_1, \ldots, m_n$| stemming from the form of the gradient of (3), Heinze & Schemper (2002) conjectured that finiteness of the reduced-bias estimates holds for every combination of data and logistic regression model. Heinze & Schemper (2002) also observed that the reduced-bias estimates are typically smaller in absolute value than the corresponding maximum likelihood estimates when the latter are finite. These observations are in agreement with the asymptotic bias of the maximum likelihood estimator in logistic regressions being approximately collinear with the parameter vector (see, e.g., Cordeiro & McCullagh, 1991).

Example 1 illustrates the finiteness and shrinkage properties of the maximum penalized likelihood estimator in the context of estimating the strengths of NBA basketball teams using a Bradley–Terry model (Bradley & Terry, 1952).

 

Example 1.

Suppose that |$y_{ij} = 1$| when team |$i$| beats team |$j$| and |$y_{ij} = 0$| otherwise. The Bradley–Terry model assumes that the contest outcome |$y_{ij}$| is the realization of a Bernoulli random variable with probability |$\pi_{ij} = \exp(\beta_i - \beta_j)/\{1 + \exp(\beta_i - \beta_j)\}$| and that the outcomes of the available contests are independent. The Bradley–Terry model is a logistic regression with probabilities as in (1), for the particular |$X$| matrix whose rows are indexed by contest identifiers |$(i, j)$| and whose general element is |$x_{ij,t} = \delta_{it} - \delta_{jt}\ (t = 1, \ldots, p)$|⁠. Here, |$\delta_{it}$| is the Kronecker delta, taking value 1 when |$t = i$| and value 0 otherwise. The parameter |$\beta_t$| can be thought of as measuring the ability or strength of team |$t$|  |$(t = 1, \ldots, p)$|⁠. Only contrasts are estimable, and an identifiable parameterization can be achieved by setting one of the abilities to zero. See, for example, Agresti (2013, § 11.6) for a general discussion of the model.

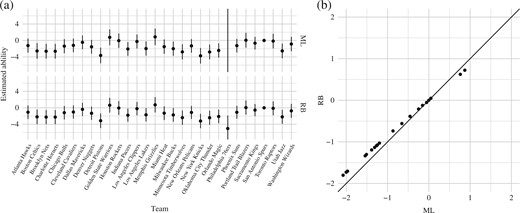
We use the Bradley–Terry model to estimate the abilities of basketball teams from game outcomes in the regular season of the 2014–2015 NBA conference. For illustrative purposes, we use only the 262 games that took place before 3 December 2014, up to which date the Philadelphia 76ers had recorded 17 straight losses and no win. The dataset was obtained from www.basketball-reference.com and is provided in the Supplementary Material. The ability of the San Antonio Spurs, the champion team of the 2013–2014 conference, is set to zero, so that each |$\beta_i$| represents the contrast of the ability of team |$i$| with that of the San Antonio Spurs. The model is estimated via iteratively reweighted least squares, as implemented in the glm function of R (R Development Core Team, 2021) with default settings for the optimization. No warnings or errors were returned during the fitting process.

The top part of Fig. 1(a) shows the reported maximum likelihood estimates of the contrasts, along with their corresponding nominally 95% individual Wald-type confidence intervals. The contrast for the Philadelphia 76ers stands out in the output from glm, with a value of |$-19.24$| and a corresponding estimated standard error of |$844.97$|⁠. These values are in fact representations of |$-\infty$| and |$\infty$|⁠, respectively, as confirmed by the detect_separation method of the R package brglm2 (Kosmidis, 2020), which implements separation-detection algorithms from a 2007 University of Oxford Department of Statistics PhD thesis by K. Konis. The data are separated, with the maximum likelihood estimates for all teams being finite except that for the Philadelphia 76ers, which is |$-\infty$|⁠. A particularly worrying side-effect of data separation here is that if the computer output is used naively, a Wald test for difference in ability between the Philadelphia 76ers and the San Antonio Spurs results in no apparent evidence of a difference, which is counterintuitive given that the former had no wins in 17 games and the latter had 13 wins in 17 games. In contrast, the reduced-bias estimates in the bottom part of Fig 1(a) all have finite values and finite standard errors. Figure 1(b) illustrates the shrinkage of the reduced-bias estimates towards zero, which has also been discussed in a range of different settings, such as in Heinze & Schemper (2002) and Zorn (2005).

Fig. 1.

(a) Estimated contrasts in ability of NBA teams with the San Antonio Spurs. The abilities are estimated using a Bradley–Terry model on the outcomes of the 262 games before 3 December 2014 in the regular season of the 2014–2015 NBA conference, using the maximum likelihood (ML, top) and reduced-bias (RB, bottom) estimators; the vertical line segments represent nominally 95% Wald-type confidence intervals. (b) Reduced-bias estimates of ability contrasts plotted against maximum likelihood estimates of ability contrasts; the maximum likelihood estimate for the Philadelphia 76ers is not plotted, and the |$45^\circ$| line is displayed for reference.

The apparent finiteness and shrinkage properties of the reduced-bias estimator, together with the fact that the estimator has the same first-order asymptotic distribution as the maximum likelihood estimator, are key reasons for the increasingly widespread use of Jeffreys-prior penalized logistic regression in applied work. At the time of writing, Google Scholar recorded approximately 2700 citations of Firth (1993), more than half of which were from 2015 or later. The list of application areas is diverse, including agriculture and fisheries research, animal and plant ecology, criminology, commerce, economics, psychology, health and medical sciences, politics, and many more. The particularly strong uptake of the method in health and medical sciences and in politics stems largely from the works of Heinze & Schemper (2002) and Zorn (2005), respectively. The reduced-bias estimator is also implemented in dedicated open-source software, such as the brglm2 (Kosmidis, 2020) and logistf (Heinze & Ploner, 2018) R packages, and it has now become part of textbook treatments of logistic regression; see, for example, Agresti (2013, § 7.4) or Hosmer et al. (2013, § 10.3).

However, a definitive theoretical account of the empirically evident finiteness and shrinkage properties has yet to appear in the literature. Such a formal account is much needed, particularly in light of recent advances that demonstrate benefits of the reduced-bias estimator in wider contexts than the ones for which it was originally developed. An example of such an advance is the work of Lunardon (2018), which explores the performance of bias reduction in stratified settings and shows that it is particularly effective for inference about a low-dimensional parameter of interest in the presence of high-dimensional nuisance parameters. For the estimation of high-dimensional logistic regression models with |$p/n \to \kappa \in (0, 1)$|⁠, experiments reported in the supplementary information of Sur & Candès (2019), see also the Supplementary Material for the present article, show that bias reduction performs similarly to their newly proposed method and markedly better than maximum likelihood. These new theoretical and empirical results justify and motivate the use of the reduced-bias estimator in even more complex applied settings than that covered by the framework of Firth (1993); in such settings, more involved methods such as modified profile likelihoods (see, e.g., Sartori (2003)) and approximate message-passing algorithms (see, e.g., Sur & Candès (2019)) have also been proposed for recovering inferential accuracy.

In this article we formally derive the finiteness and shrinkage properties of reduced-bias estimators for logistic regressions under only the condition that the model matrix |$X$| has full rank. We also provide geometric insights into how penalized likelihood estimators shrink towards zero and discuss the implications of finiteness and shrinkage for inference, especially with regard to hypothesis tests and confidence regions using Wald-type procedures.

We show how the results can be extended in a direct way to other commonly used link functions, such as the probit, log-log, complementary log-log and cauchit links, whenever the Jeffreys prior is used as a likelihood penalty. The work presented here thus complements earlier work of Ibrahim & Laud (1991) and especially Chen et al. (2008), which considers the same models from a Bayesian perspective. Here we study the behaviour of the posterior mode and thereby derive results that add to those earlier findings, whose focus was instead on important Bayesian aspects such as propriety and moments of the posterior distribution.

The results in this paper also extend readily to situations where penalized loglikelihoods of the form

$$\begin{equation} \label{penloglika} l^\dagger(\beta; a) = l(\beta) + a \log\bigl| X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)X\bigr| \quad (a > 0) \end{equation}$$

(4)

are used, with |$a$| allowed to take values other than |$1/2$|⁠. Such penalized loglikelihoods have proven useful in prediction contexts, where the value of |$a$| can be tuned to deliver better estimates of the binomial probabilities, and they are the subject of ongoing research (see, e.g., Elgmati et al., 2015; Puhr et al., 2017). The procedure of repeated maximum likelihood fits with iteratively adjusted binomial responses and totals, derived in § 4, maximizes |$l^\dagger(\beta; a)$| for general binomial-response generalized linear models and any |$a>0$|⁠.

2. Logistic regression

2.1. Finiteness

We first derive results on finiteness and shrinkage of the maximum penalized likelihood estimator for logistic regression, which is the most common case in applications and also the case for which maximum penalized likelihood, with the Jeffreys-prior penalty, coincides with asymptotic bias reduction. These results provide a platform for the generalization to link functions other than logit in § 3.

Let |$W^*(r)$| be |$W(\beta)$| at |$\beta = \beta(r)$|⁠, for |$r\in \mathbb{R}$|⁠, where |$\beta(r)$| is a path in |$\mathbb{R}^p$| such that |$\beta(r) \to \beta_0$| as |$r \to \infty$|⁠, with |$\beta_0$| having at least one infinite component. Theorem 1 below describes the limiting behaviour of the determinant of the expected information matrix |$X^{{ \mathrm{\scriptscriptstyle T} }} W^*(r) X$| as |$r$| diverges to infinity, under only the assumption that |$X$| has full rank. An important implication of Theorem 1 is Corollary 1, which says that the reduced-bias estimators for logistic regressions are always finite. These new results formalize a sketch argument made in Firth (1993, § 3.3).

 

Theorem 1.

Suppose that |$X$| is of full rank. Then |$\lim_{r \to \infty} |X^{{ \mathrm{\scriptscriptstyle T} }} W^*(r)X| = 0$|⁠.

 

Corollary 1.

Suppose that |$X$| is of full rank. The vector |$\tilde\beta$| that maximizes |$\tilde{l}(\beta)$| has all of its components finite.

The proofs of Theorem 1 and Corollary 1 are given in the Supplementary Material.

Corollary 1 also holds for any fixed |$a > 0$| in (4). As a result, the maximum penalized likelihood estimators from the maximization of |$l^\dagger(\beta; a)$| in (4) have finite components for any |$a > 0$|⁠.

Despite its practical utility, the finiteness of the reduced-bias estimator results in some notable, and perhaps undesirable, side-effects for Wald-type inferences based on the reduced-bias estimator that have been largely overlooked in the literature. The finiteness of |$\tilde\beta$| implies that the estimated standard errors |$s_t(\tilde{\beta})$|  |$(t = 1, \ldots, p)$|⁠, calculated as the square roots of the diagonal elements of the inverse of |$X^{{ \mathrm{\scriptscriptstyle T} }} W(\tilde\beta)X$|⁠, are also always finite. Since |$y_1, \ldots, y_n$| are realizations of binomial random variables, there is only a finite number of values that the estimator |$\tilde\beta$| can take for any given |$x_1, \ldots, x_n$|⁠. Hence, there will always be a parameter vector with large enough components that the usual Wald-type confidence intervals |$\tilde\beta_t \pm z_{1 - \alpha/2} s_t(\tilde\beta)$|⁠, or confidence regions in general, will fail to cover regardless of the nominal level |$\alpha$| that is used. This phenomenon has also been observed in the complete enumerations of Kosmidis (2014) for proportional odds models which are extensions of logistic regression to ordinal responses; and it is also the case when the penalized likelihood is profiled for the construction of confidence intervals, as proposed, for example, in Heinze & Schemper (2002), and in Bull et al. (2007) for multinomial regression models.

2.2. Shrinkage

The following theorem is key when exploring the shrinkage properties of the reduced-bias estimator that have been illustrated in Example 1.

 

Theorem 2.

Suppose that |$X$| is of full rank. Then the following hold.  

• (i) The function |$|X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)X|$| is globally maximized at |$\beta = 0$|⁠.

• (ii) If |$\bar{W}(\pi) = \mathop{\rm diag}\{m_1\pi_1(1-\pi_1), \ldots, m_n\pi_n(1-\pi_n)\}$|⁠, then |$|X^{{ \mathrm{\scriptscriptstyle T} }} \bar{W}(\pi)X|$|  is log-concave on |$\pi$|⁠.

A complete proof of Theorem 2 is given in the Supplementary Material. Part (i) also follows directly from Theorem 1 in Chen et al. (2008).

Consider estimation by maximization of the penalized loglikelihood |$l^\dagger(\beta; a)$| in (4) for |$a = a_1$| and |$a = a_2$| with |$a_1 > a_2 \ge 0$|⁠. Let |$\beta^{(a_1)}$| and |$ \beta^{(a_2)}$| be the maximizers of |$l^\dagger(\beta; a_1)$| and |$l^\dagger(\beta; a_2)$|⁠, respectively, and |$ \pi^{(a_1)}$| and |$ \pi^{(a_2)}$| the corresponding estimated |$n$|-vectors of probabilities. Then, by the concavity of |$\log|X^{{ \mathrm{\scriptscriptstyle T} }} \bar{W}( \pi)X|$|⁠, the vector |$ \pi^{(a_1)}$| is closer to |$(1/2, \ldots, 1/2)^{{ \mathrm{\scriptscriptstyle T} }}$| than is |$ \pi^{(a_2)}$|⁠, in the sense that |$ \pi^{(a_1)}$| lies within the hull of that convex contour of |$\log |X^{{ \mathrm{\scriptscriptstyle T} }}\bar{W}( \pi)X|$| containing |$ \pi^{(a_2)}$|⁠. With the specific values |$a_1=1/2$| and |$a_2=0$|⁠, the last result refers to maximization of the likelihood penalized by Jeffreys’ prior and to maximization of the unpenalized likelihood, respectively. Hence, using reduced-bias estimators for logistic regressions has the effect of shrinking towards the model that implies equiprobability across observations, relative to maximum likelihood. Shrinkage here is with respect to a metric based on the expected information matrix rather than with respect to Euclidean distance. Hence, the reduced-bias estimates are only typically, rather than always, smaller in absolute value than the corresponding maximum likelihood estimates.

If the determinant of the inverse of the expected information matrix is taken as a generalized measure of the asymptotic variance, then the estimated generalized asymptotic variance at the reduced-bias estimates is always smaller than the corresponding estimated variance at the maximum likelihood estimates. Hence, approximate confidence ellipsoids based on asymptotic normality of the reduced-bias estimator are reduced in volume.

3. Non-logistic link functions

3.1. Finiteness

The results in this section generalize those of § 2.1 and § 2.2 beyond the logit link function, still for estimators from penalized likelihoods of the form (4). For non-logistic link functions, such estimators no longer coincide with the bias-reduced estimator of Firth (1993).

Theorem 1 and Corollary 1 readily extend to link functions other than the logistic one. Specifically, if |$G(\eta) = \exp(\eta)/\{1 + \exp(\eta)\}$| in model (1) is replaced by an at least twice differentiable and invertible function |$G: \mathbb{R} \to (0, 1)$|⁠, then the expected information matrix again has the form |$X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)X$|⁠, but with working weights |$w_i(\beta) = m_i(\omega \circ \eta_i)(\beta)$|  |$(i = 1, \ldots, n)$|⁠, where |$\omega(\eta) = g(\eta)^2/[G(\eta)\{1 - G(\eta)\}]$| and |$g(\eta) = {\rm d} G(\eta)/{\rm d}\eta$|⁠. If the link function is such that |$\omega(\eta) \to 0$| as |$\eta$| diverges to either |$-\infty$| or |$\infty$|⁠, then the proofs of Theorem 1 and Corollary 1 in the Supplementary Material carry through unaltered to show that |$\lim_{r \to \infty} |X^{{ \mathrm{\scriptscriptstyle T} }} W^*(r)X| = 0$| and that, when the penalty is a positive power of Jeffreys’ invariant prior, the maximum penalized likelihood estimates have finite components. The logit, probit, complementary log-log, log-log and cauchit links are some commonly used link functions for which |$\omega(\eta) \to 0$|⁠. The functions |$G(\eta)$| and |$\omega(\eta)$| for each of these link functions are shown in Table 1.

Table 1.

Common link functions and the corresponding forms for |$G(\eta)$| and |$\omega(\eta)$|⁠; for all the displayed link functions, |$\omega(\eta)$| vanishes as |$\eta$| diverges

Link function	|$G(\eta)$|	|$\omega(\eta)$|
logit	|$\displaystyle \frac{\exp(\eta)}{1 + \exp(\eta)}$|	|$\displaystyle \frac{\exp(\eta)}{\{1 + \exp(\eta)\}^2}$|
probit	|$\displaystyle \Phi(\eta)$|	|$\displaystyle \frac{\{\phi(\eta)\}^2}{\Phi(\eta)\{1- \Phi(\eta)\}}$|
complementary log-log	|$\displaystyle 1 - \exp\{-\exp(\eta)\}$|	|$\displaystyle \frac{\exp(2 \eta)}{\exp\{\exp(\eta)\}-1}$|
log-log	|$\displaystyle \exp\{-\exp(- \eta)\}$|	|$\displaystyle \frac{\exp(-2 \eta)}{\exp\{\exp(-\eta)\}-1}$|
cauchit	|$\displaystyle \frac{1}{2} + \frac{\arctan(\eta)}{\pi}$|	|$\displaystyle \frac{1}{(1 + \eta^2)^2 \bigl[\frac{\pi^2}{4} - \{\tan^{-1}(\eta)\}^2 \bigr]}$|

3.2. Shrinkage

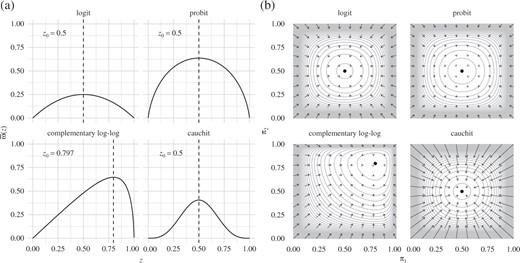
Let |$\bar{\omega}(z) = \{(g \circ G^{-1})(z)\}^2/\{z(1 - z)\}$|⁠. If the link function is such that |$\bar{\omega}(z)$| is maximized at some value |$z_0 \in (0, 1)$|⁠, then the same arguments as in the proof of Theorem 2(i) can be used to show that |$|X^{{ \mathrm{\scriptscriptstyle T} }} \bar{W}(\pi)X|$| is globally maximized at |$(z_0, \ldots, z_0)^{{ \mathrm{\scriptscriptstyle T} }}$|⁠. Figure 2(a) illustrates that this condition is satisfied for the logit, probit, log-log and complementary log-log link functions. If |$x_{i1} = 1$|  |$(i = 1, \ldots, n)$|⁠, then the maximum of |$|X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)X|$| is achieved at |$\beta = (b_0, 0, \ldots, 0)^{{ \mathrm{\scriptscriptstyle T} }}$|⁠, where |$b_0 = g^{-1}(z_0)$|⁠. Moreover, it can be seen directly from the proof of Theorem 2 that a sufficient condition for the log-concavity of |$|X^{{ \mathrm{\scriptscriptstyle T} }} \bar{W}(\pi)X|$| for non-logit link functions is that |$\bar{\omega}(z)$| is concave.

Fig. 2.

(a) |$\bar{\omega}(z)$| for various link functions; in each plot the dashed vertical line is at |$z_0$|⁠. (b) Demonstration of how fitted probabilities from the penalized likelihood fit shrink relative to those of the maximum likelihood fit, from a complete enumeration of a saturated model with |$\pi_i = G(\beta_1 + \beta_2 x_i)$|  |$(i = 1, 2)$|⁠, where |$x_1 = -1$| and |$x_2 = 1$|⁠, and with |$m_1 = 9$| and |$m_2 = 9$|⁠; the arrows point from the estimated probabilities based on the maximum likelihood estimates to those based on the penalized likelihood estimates, and the grey curves are the contours of |$\log|X^{{ \mathrm{\scriptscriptstyle T} }} \bar{W}(\pi)X|$|⁠.

4. Maximum penalized likelihood as repeated maximum likelihood

The maximum penalized likelihood estimates, when |$X$| has full rank, can be computed by direct numerical optimization of the penalized loglikelihood |$l^\dagger(\beta; a)$| in (4) or by using a quasi-Newton–Raphson iteration as in Kosmidis & Firth (2010). Nevertheless, the particular form of the Jeffreys prior allows the convenient computation of penalized likelihood estimates by leveraging readily available maximum likelihood implementations for binomial-response generalized linear models.

If |$G(\eta) = \exp(\eta) / \{1 + \exp(\eta)\}$| in model (1) is replaced by any invertible function |$G: \mathbb{R} \rightarrow (0, 1)$| that is at least twice differentiable, then differentiation of |$l^\dagger(\beta; a)$| with respect to |$\beta_t$|  |$(t = 1, \ldots, q)$| gives that the penalized likelihood estimates are the solutions to

$$\begin{equation} \label{scores_jeffreys} \sum_{i = 1}^n \frac{w_i(\beta)}{d_i(\beta)} \left[ y_i + 2 a h_i(\beta) \left\{ q_i(\beta) - \frac{1}{2} \right\} - m_i \pi_i(\beta) \right] x_{it} = 0 \quad (t = 1, \ldots, p) , \end{equation}$$

(5)

where |$\pi_i(\beta) = (G \circ \eta_i)(\beta)$|⁠, |$d_i(\beta) = m_i (g \circ \eta_i)(\beta)$|⁠, |$q_i(\beta) = d_i'(\beta)/w_i(\beta) + \pi_i(\beta)$|⁠, and |$d_i'(\beta) = m_i (g' \circ \eta_i)(\beta)$| with |$g'(\eta) = {\rm d}^2 G(\eta) / {\rm d}\eta^2$|⁠. The quantity |$h_i(\beta)$|  |$(i = 1, \ldots, n)$| is the |$i$|th diagonal element of the ‘hat’ matrix |$H(\beta) = X \{X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta) X\}^{-1} X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta)$|⁠.

If we temporarily omit the observation index and suppress the dependence of the various quantities on |$\beta$|⁠, the derivatives of |$l^\dagger(\beta; a)$| are the derivatives of the binomial loglikelihood |$l(\beta)$| with link function |$G(\eta)$|⁠, after adjusting the binomial response |$y$| to |$y + 2 a h (q - 1/2)$|⁠. Hence, the penalized likelihood estimates can be conveniently computed through repeated maximum likelihood fits, where each repetition consists of two steps: (i) the adjusted responses are computed at the current parameter values; and (ii) the maximum likelihood estimates of |$\beta$| are computed at the current value of the adjusted responses.

However, depending on the sign and magnitude of |$2 a h (q - 1/2)$|⁠, the adjusted response can be either negative or greater than the binomial total |$m$|⁠. In such cases, standard implementations of maximum likelihood either are unstable or report an error. This is because the binomial loglikelihood is not necessarily concave when |$y < 0$| or |$y > m$| for at least one observation, if a link function with concave |$\log\{G(\eta)\}$| and |$\log\{1 - G(\eta)\}$| is used. The logit, probit, log-log and complementary log-log link functions are of this kind. See, for example, Pratt (1981, § 5) for results and discussion on concavity of the loglikelihood.

Such issues with the use of repeated maximum likelihood fits can be avoided by noting that expression (5) results if, in the derivatives of the loglikelihood, |$y$| and |$m$| are replaced by their adjusted versions

$$\begin{equation} \label{pseudodatay} \tilde{y} = y + 2 a h (q - 1/2 + \pi c ), \quad \tilde{m} = m + 2 a h c . \end{equation}$$

(6)

Here |$c$| is some arbitrarily chosen function of |$\beta$|⁠. The following theorem identifies one function |$c$| for which |$0 \le \tilde{y} \le \tilde{m}$|⁠.

 

Theorem 3.

Let |$I(A)$| be equal to |$1$| if |$A$| holds and |$0$| otherwise. If |$c = 1 + (q - 1/2)\{ \pi - I(q \le 1/2) \}/\{\pi(1 - \pi)\}$|⁠, then |$0 \le \tilde{y} \le \tilde{m}$|⁠.

The proof of Theorem 3 is given in the Supplementary Material, which also provides pseudo-code and R code for the algorithm JeffreysMPL that implements repeated maximum likelihood fits to maximize |$l^\dagger(\beta; a)$| for any supplied |$a$| and link function |$G(\eta)$|⁠.

The variance-covariance matrix of the penalized likelihood estimator can be obtained as |$(R^{{ \mathrm{\scriptscriptstyle T} }} R)^{-1}$|⁠, where |$R$| is the upper triangular matrix from the QR decomposition of |$W(\beta)^{1/2} X$| at the final iteration of the procedure. That decomposition is a by-product of the algorithm JeffreysMPL.

If, in addition to |$X$| having of full rank, we require that |$X$| has a column of ones and that |$g(\eta)$| is a unimodal density function, it can be shown that if the starting value of the parameter vector |$\beta$| in the repeated maximum likelihood fits procedure has finite components, then the values of |$\beta$| computed in step (ii) will also have finite components at all repetitions. This is because, with a column of ones in the full-rank |$X$|⁠, the adjusted responses and totals in (6) satisfy |$0 < \tilde{y} < \tilde{m}$|⁠, and hence maximum likelihood estimates with infinite components are not possible. The strict inequalities |$0 < \tilde{y} < \tilde{m}$| hold because, under the aforementioned conditions, |$w_i(\beta) > 0$| and |$X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta) X$| is positive definite for |$\beta$| with finite components. Then, Theorem 4 in (Magnus & Neudecker (1999), Ch. 11) on bounds for the Rayleigh quotient gives the inequality |$h_i(\beta) \ge w_i(\beta) x_i^{{ \mathrm{\scriptscriptstyle T} }} x_i \lambda(\beta) > 0$|  |$(1, \ldots, n)$|⁠, where |$\lambda(\beta) > 0$| is the minimum eigenvalue of |$(X^{{ \mathrm{\scriptscriptstyle T} }} W(\beta) X)^{-1}$|⁠.

The repeated maximum likelihood fits procedure has the correct fixed point even if in step (ii) full maximum likelihood estimation is replaced by a procedure that merely increases the loglikelihood, such as a single step of iteratively reweighted least squares for the adjusted responses and totals. Firth (1992) suggested such a scheme for logistic regressions with |$a = 1/2$|⁠. There is currently no conclusive result on whether full maximum likelihood iteration with a reasonable stopping criterion is better or worse than, for example, one step of iteratively reweighted least squares in terms of computational efficiency. A satisfactory starting value for the above procedure is the maximum likelihood estimate of |$\beta$|⁠, after adding a small positive constant and twice that constant to the actual binomial responses and totals, respectively.

Finally, for |$a = 1/2$|⁠, repeated maximum likelihood fits can be used to compute the posterior normalizing constant when implementing the importance sampling algorithm in Chen et al. (2008, § 5) for posterior sampling of the parameters of Bayesian binomial-response generalized linear models with the Jeffreys prior.

The Supplementary Material illustrates the evolution of adjusted responses and totals through the iterations of JeffreysMPL, for the first six games of the Philadelphia 76ers in Example 1. We also compute the reduced-bias estimates for a logistic regression model with |$n = 1000$| binary responses and |$p = 200$| covariates, as considered in Fig. 2(b) of the supplementary information appendix of Sur & Candès (2019), and show that such computation takes only a couple of seconds on a standard laptop computer.

5. Illustrations

Figure 2(a) shows |$\bar{\omega}(z)$| and |$z_0$| for the various link functions. The plot for the log-log link is the reflection of the one for the complementary log-log link in |$z = 0.5$|⁠. As is apparent, |$\bar{\omega}(z)$| is concave for the logit, probit and complementary log-log links, but not for the cauchit link. Figure 2(b) visualizes the shrinkage induced by the penalization by Jeffreys’ invariant prior for the logit, probit, complementary log-log and cauchit links. For each link function, we obtain all possible fitted probabilities from a complete enumeration of a saturated model with |$\pi_i = G(\beta_1 + \beta_2 x_i)$|  |$(i = 1, 2)$|⁠, where |$x_1 = -1$|⁠, |$x_2 = 1$|⁠, |$m_1 = 9$| and |$m_2 = 9$|⁠. The grey curves are the contours of |$\log|X^{{ \mathrm{\scriptscriptstyle T} }}\bar{W}(\pi)X|$|⁠. An arrow is drawn from each pair of estimated probabilities based on the maximum likelihood estimates to the corresponding pair of estimated probabilities based on the penalized likelihood estimates, to demonstrate the induced shrinkage towards |$(z_0, z_0)^{{ \mathrm{\scriptscriptstyle T} }}$| according to the results in § 3. Despite the fact that |$\bar\omega(z)$| is not concave for the cauchit link, the fitted probabilities still shrink towards |$(z_0, z_0)^{{ \mathrm{\scriptscriptstyle T} }} = (1/2, 1/2)^{{ \mathrm{\scriptscriptstyle T} }}$|⁠. The plots in Fig. 2 are invariant with respect to the particular choices of |$x_1$| and |$x_2$|⁠, as long as |$x_1 \ne x_2$|⁠. For either maximum likelihood or maximum penalized likelihood, if the estimates of |$\beta_1$| and |$\beta_2$| are |$b_1$| and |$b_2$| for |$x_1 = -1$| and |$x_2 = 1$|⁠, then the new estimates for any |$x_1, x_2 \in \mathbb{R}$| with |$x_1 \ne x_2$| are |$b_1 - b_2 (x_1 + x_2) / (x_2 - x_1)$| and |$2 b_2 / (x_2 - x_1)$|⁠, respectively. Hence, the fitted probabilities will be identical.

Another illustration of finiteness and shrinkage follows from Example 1. Figure 3 shows the paths of the team ability contrasts as |$a$| varies from |$0$| to |$5$|⁠. The estimates are obtained using JeffreysMPL, starting at the maximum likelihood estimates of the ability contrasts after adding |$0.01$| and |$0.02$| to the actual responses and totals, respectively. In accordance with the theoretical results in § 2.1, the estimated ability contrasts are finite for every |$a > 0$|⁠; and, as expected from the results in § 2.2, shrinkage towards equiprobability becomes stronger as |$a$| increases.

Fig. 3.

Paths of the estimated ability contrasts from the maximization of (4) for |$a \in (0, 5]$|⁠; in each plot the dashed horizontal line is at zero and the dotted vertical line is at |$a = 0.5$|⁠, identifying the reduced-bias estimates on the paths.

6. Concluding remarks

A recent stream of literature investigates the use of the coefficient path defined by maximization of the penalized loglikelihood (4) for the prediction of rare events through logistic regression. Elgmati et al. (2015) studied that path for |$a \in (0, 1/2]$| and proposed taking |$a$| to be around |$0.1$| in order to handle issues related to infinite estimates, and they obtained predicted probabilities that are less biased than those based on the reduced-bias estimates (⁠|$a = 0.5$|⁠). More recently, Puhr et al. (2017) proposed two new methods for the prediction of rare events, and performed extensive simulation studies to compare the performance of their methods and various others, including maximum penalized likelihood with |$a = 0.1$| and |$a = 0.5$|⁠.

The coefficient path can be computed efficiently by using repeated maximum likelihood fits with warm starts. For a grid of values |$a_1 < \cdots < a_k$| with |$a_j > 0$|  |$(j = 1, \ldots, k)$|⁠, the algorithm JeffreysMPL is first applied with |$a = a_1$| to obtain the maximum penalized likelihood estimates |$\beta^{(a_1)}$|⁠; then JeffreysMPL is applied again with |$a = a_2$| and starting values |$b = \beta^{(a_1)}$|⁠, and so on, until |$\beta^{(a_k)}$| has been computed. This process supplies JeffreysMPL with the best available starting values as the algorithm walks through the grid. The finiteness of the components of |$\beta^{(a_1)}, \ldots, \beta^{(a_k)}$| and the shrinkage properties described in § 2.2 and § 3 contribute to the stability of the overall process. The properties of the coefficient path for inference and prediction from binomial regression models, and the development of general procedures for selecting |$a$|⁠, are interesting open research topics.

Kenne Pagui et al. (2017) developed a method that can reduce the median bias of the components of the maximum likelihood estimator. According to their results, median bias reduction for one-parameter logistic regression models is equivalent to maximizing (4) with |$a = 1/6$|⁠. Hence, the results in § 2 also establish the finiteness of the estimate from median bias reduction in one-parameter logistic regression, and imply that the induced shrinkage to equiprobability will be less strong than penalization by the Jeffreys prior. Kenne Pagui et al. (2017) observed such properties in numerical studies for |$p > 1$|⁠. When |$p > 1$|⁠, though, median bias reduction is no longer equivalent to maximizing (4) with |$a = 1/6$|⁠.

Acknowledgement

The authors are affiliated with The Alan Turing Institute and were supported by the U.K. Engineering and Physical Sciences Research Council, EPSRC, under grant EP/N510129/1. Firth was also partly supported by the EPSRC programme ‘Intractable Likelihood: New Challenges from Modern Applications’ under grant EP/K014463/1.

Supplementary material

Supplementary material available at Biometrika online includes proofs of Theorems 1–3 and Corollary 1, the algorithm JeffreysMPL, additional numerical results, and R code and data to reproduce all of the numerical work and graphs.