Base Manifolds for Lagrangian Fibrations on Hyperkähler Manifolds

Abstract

Let f : X→B be a fibration from a hyperkähler manifold to a complex space B. Assuming that B is smooth, we show that ⁠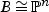. This generalizes a theorem of Hwang to the Kähler case.

1 Introduction

One of the most important and startling conjectures in the study of hyperkähler manifolds X says that the base space of any nontrivial fibration X→B is the complex projective space ⁠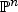, where ⁠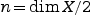. We refer the reader to [3, Section 21.4] for a discussion of this conjecture. Any such fibration is automatically Lagrangian with respect to the holomorphic symplectic form by works of Matsushita; see [9] or Section 2 for a summary of his results.

With the additional hypothesis that X be projective and that B be smooth, the conjecture is known to hold by work of Hwang [4]. In this short note, we remove Hwang’s projectivity assumption on X, and prove the following result.

 

Theorem 1.1

Let X be a hyperkähler manifold, and let f : X→B be a fibration onto a complex space B. If B is smooth, then ⁠.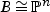

Our proof is a simple combination of fundamental results due to Fujiki [2], Hwang [4], Matsushita [9, 10], and Siu [11]: after noting that the base manifold has to be projective, we pull back a very ample line bundle from B to X and use this line bundle to deform the given fibration to a sequence of projective ones. Then, we apply Hwang’s theorem to these projective deformations and use global deformation rigidity of 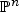to conclude the desired result for the central fiber.

2 Preliminaries

We start by fixing our notation and by recalling definitions of the basic objects investigated in this note.

 

Definition 2.1

A compact Kähler manifold is called hyperkähler or irreducible holomorphic symplectic if it is simply connected, and if ⁠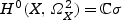, where σ is everywhere nondegenerate. A fibration on X is a (proper) surjective holomorphic map f: X → B with 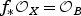from X to a complex space B with ⁠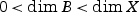. In particular, the base B of a fibration is normal, and f has connected fibers. A Lagrangian fibration on X is a fibration f:X→B such that every irreducible component of every fiber of f is a Lagrangian subvariety with respect to the holomorphic symplectic form σ.

To make this note more self-contained, we collect some known results concerning fibrations on hyperkähler manifolds, which we will use in the subsequent proof, in the following proposition.

 

Proposition 2.2

Let X be a hyperkähler manifold of dimension 2n, and let f : X→B be a fibration onto a normal complex space B. Then, f is a Lagrangian fibration onto a normal projective variety. In particular, B has dimension n.

 

Proof

As explained in [1, Theorem 1] and footnote, using results of Varouchas [12, 13] and the fundamental results of Matsushita [6–8], one shows without any a priori assumption on the base of the fibration that B is a normal Kähler space. Then, [9, Theorem 2.1 and 3.1] imply the claim.

3 Proof of Theorem 1.1

Let X be a hyperkähler manifold of dimension 2n, and let f : X→B be a fibration onto a smooth complex space B.

Since B is projective by Proposition 2.2, there exists a very ample line bundle on B. Let L denote its pullback under f. Furthermore, let 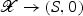be the (smooth) Kuranishi space of X; in particular, 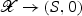is a smooth family of hyperkähler manifolds. By work of Matsushita [10, Theorem 1.1(1) and 1.1(2)], there exists a smooth hypersurface (S_L,0) in (S,0), and a line bundle 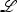on the pullback 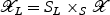of 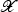to S_L such that the restriction of 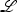to the fiber over the reference point 0 is isomorphic to L. We denote the natural projection 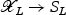by p, and we note that both 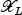as well as p are smooth. As usual we will take a representative of the germ (S_L,0) and shrink it if necessary (keeping the base point), usually without mentioning this explicitly.

By [10, Theorem 1.1(3) and Corollary 1.2] the pushforward 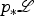is a vector bundle, the canonical map 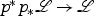is surjective, and thus gives rise to a morphism 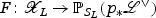over S_L that extends f : X→B to the whole family ⁠.

 

Lemma 3.1

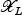We have b₂(X)≥4. In particular, S_L has positive dimension.

 

Proof

Let α be a Kähler class on X. Since L is not ample, its Chern class is not a multiple of α, hence h^1,1(X)≥2, implying the first claim. For the second claim, note that the dimension of the Kuranishi space S of X is ⁠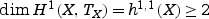, and that S_L is a hyperplane in S.

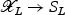So is a positive-dimensional smooth family of hyperkähler manifolds. Restricting the family 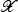to a general smooth embedded disk Δ⊂S_L through the origin, we obtain a commutative diagram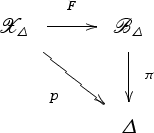

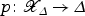(3.1)

where is a smooth family of hyperkähler manifolds with smooth total space, and 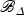is the scheme–theoretic image of the fibration induced by a sufficiently high tensor power of ⁠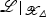. Note that 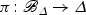is a flat family with normal total space.

 

Lemma 3.2

The scheme–theoretic fiber 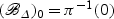is reduced, hence smooth.

 

Proof

Since 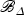is normal, it is nonsingular at general points of the central fiber. Since p is a smooth morphism, it follows from diagram (3.1) that 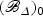is generically reduced. Let t be a coordinate on Δ. We note that π*t is not a zero divisor in any of the local rings 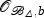of points b∈π⁻¹(0). Consequently, as 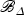satisfies Serre’s condition S₂, the scheme 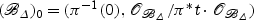does not have any embedded components, and is therefore reduced, cf. [5, p. 125]. Hence, ⁠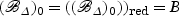, which is smooth by assumption.

Lemma 3.2 implies that 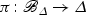is flat with smooth central fiber, hence a smooth morphism. Moreover, [2, Theorem 4.8(2)] implies that there exists a dense subset T⊂Δ such that X_t:=p⁻¹(t) is projective for all t∈T, see also [3, Proposition 26.6]. Therefore, by Hwang’s theorem [4] the fiber B_t:=π⁻¹(t) is isomorphic to 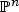for all t∈T. Hence, we find a sequence of points 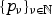in T⊂Δ such that ⁠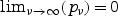, and such that ⁠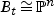. Hence, global deformation rigidity of ⁠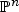, see [11], paragraph following the Main Theorem implies that the central fiber is likewise isomorphic to ⁠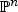. This concludes the proof of Theorem 1.1.

Funding

The first-named author gratefully acknowledges support by the Baden-Württemberg Stiftung through the “Eliteprogramm für Postdoktorandinnen und Postdoktoranden”, as well as by the DFG-Research Training Group GK 1821 “Cohomological methods in geometry”. The second-named author was supported by the LABEX IRMIA, Strasbourg.

Acknowledgements

The authors are grateful to Sönke Rollenske for helpful discussions, and to Tim Kirschner, whose questions led to significant improvements in the exposition of our arguments. Moreover, the authors thank the anonymous referees for helpful comments and remarks.