Arithmetic Properties of the Frobenius Traces Defined by a Rational Abelian Variety (with two appendices by J-P. Serre)

Abstract

Let |$A$| be an abelian variety over |$\mathbb Q$| of dimension |$g$| such that the image of its associated absolute Galois representation |$\rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{ \mathbb Z})$|⁠. We investigate the arithmetic of the traces |$a_{1, p}$| of the Frobenius at |$p$| in |$\operatorname{Gal}(\overline{\mathbb Q}/\mathbb Q)$| under |$\rho_A$|⁠. In particular, we obtain upper bounds for the counting function |$\#\{p \leq x: a_{1, p} = t\}$| and we prove an Erdös-Kac-type theorem for the number of prime factors of |$a_{1, p}$|⁠. We also formulate a conjecture about the asymptotic behaviour of |$\#\{p \leq x: a_{1, p} = t\}$|⁠, which generalizes a well-known conjecture of Lang and Trotter from 1976 about elliptic curves.

1 Introduction

Given an abelian variety |$A/\mathbb Q$|⁠, its reductions |$A_p/\mathbb F_p$| modulo primes encode deep arithmetic global information. A primary question related to these reductions concerns their |$p$|-Weil polynomials, in particular the coefficients of these polynomials.

In the simplest case when |$A$| has dimension 1, that is, when |$A$| is an elliptic curve over |$\mathbb Q$|⁠, for each prime |$p$| of good reduction the |$p$|-Weil polynomial is |$ P_{A, p}(X) = X^2 - a_p X + p \in \mathbb Z[X], $| where |$ a_p := p + 1 - |A_p(\mathbb F_p)|. $| The coefficient |$a_p$| satisfies the Weil bound |$|a_p| < 2 \sqrt{p}$| and is of major significance in number theory. For example, it appears as the |$p$|th Fourier coefficient in the expansion of the weight 2 newform associated to |$A$|⁠. The study of |$a_p$| comes in several flavours, some having led to well-known problems in arithmetic geometry, such as the Sato-Tate Conjecture from the 1960s (now a theorem) and the Lang-Trotter Conjecture on Frobenius traces from the 1970s (still open).

Briefly, the Lang-Trotter Conjecture [35] on the behaviour of |$a_p$| predicts that for every elliptic curve |$A/\mathbb Q$| and every integer |$t \in \mathbb Z$|⁠, if |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| or |$t \neq 0$|⁠, and if we write |$N_A$| for the product of the primes of bad reduction for |$A$|⁠, then either there are at most finitely many primes |$p$| such that |$a_{p} = t$| or there exists a constant |$c(A, t) > 0$| such that, as |$x \rightarrow \infty$|⁠,

$${\pi }_A(x,t):=\#\left\{p\le x:p\nmid N_A,a_p=t\right\}~c(A,t)\frac{\sqrt{x}}{\log x}.$$

(1)

The constant |$c(A, t)$| has a precise heuristic description derived from the Chebotarev Density Theorem, combined with the Sato-Tate Conjecture when |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| and with a prime distribution law arising from works of Deuring and Hecke when |$\operatorname{End}_{\overline{\mathbb Q}}(A) \not\simeq \mathbb Z$|⁠.

While the Lang-Trotter Conjecture remains open, several remarkable related results have been proven. When |$\operatorname{End}_{\overline{\mathbb Q}}(A) \not\simeq \mathbb Z$| (the CM case) and |$t \neq 0$|⁠, upper bounds of the right order of magnitude can be proved using sieve methods. When |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| and |$t \neq 0$|⁠, weaker upper bounds, unconditional or conditional (upon the Generalized Riemann Hypothesis, GRH), can be proved using effective versions of the Chebotarev Density Theorem; such bounds were first obtained by Serre [42, Theorem 20]. The currently best unconditional upper bound, |$\pi_A(x, t) \ll_A \frac{x (\log \log x)^2}{(\log x)^2}$|⁠, was obtained by V. K. Murty [38, Theorem 5.1] (see [48] for an earlier result), while the currently best upper bound under GRH, |$\pi_A(x, t) \ll_A \frac{x^{\frac{4}{5}}}{(\log x)^{\frac{1}{5}}}$|⁠, was obtained by Murty, Murty, and Saradha [37, Theorem 4.2] (for very recent improvements on the exponent of the |$\log x$| factor, see [52]). When |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| and |$t = 0$|⁠, stronger results are known; in particular, the unconditional bounds |$\frac{\log \log \log x}{(\log \log \log \log x)^{1 + \varepsilon}} \ll_{\varepsilon} \pi_A(x, 0) \,{\ll}\, x^{\frac{3}{4}}$| were obtained by Fouvry and M. R. Murty [22, Theorem 1] and, respectively, by Elkies [19] using, as a key tool, Deuring’s characterization of supersingular primes [17].

Inspired by these works, the main goal of our article is to investigate the arithmetic of the Frobenius traces of a generic higher-dimensional abelian variety |$A/\mathbb Q$|⁠; in particular:

• (i) we will prove upper bounds for the generalization of the counting function |$\pi_A(x, t)$| and deduce results on the growth of the Frobenius traces;

• (ii) we will determine the normal order of the sequence defined by the prime divisor function of the Frobenius traces, and, more generally, we will prove an Erdös-Kac-type result for this sequence;

• (iii) under suitable hypotheses, we will formulate a generalization of (1).

Our main results mark only the beginning of such investigations in higher dimensions and we hope shall stimulate further research.

Our main setting and notation are as follows. Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$|⁠. Let |$\overline{\mathbb Q}$| denote an algebraic closure of |$\mathbb Q$| and let |$\operatorname{End}_{\overline{\mathbb Q}}(A)$| denote the endomorphism ring of |$A$| over |$\overline{\mathbb Q}$|⁠. Let |$N_A$| be the product of primes of bad reduction for |$A$|⁠.

We denote by

$${\rho }_A:\mathrm{Gal}\left(\overline{\mathbb{Q}}/\mathbb{Q}\right)\to {\mathrm{GSp}}_{2g}(\widehat{\mathbb{Z}})$$

the absolute Galois representation defined by the inverse limit of the representations

$${\overline{\rho }}_{A,m}:\mathrm{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\to {\mathrm{GSp}}_{2g}(\mathbb{Z}/m\mathbb{Z})$$

of |$\operatorname{Gal}(\overline{\mathbb Q}/\mathbb Q)$| on the |$m$|-torsion |$A[m] \subset A(\overline{\mathbb Q})$| for each integer |$m \geq 1$|⁠. For each prime |$\ell$| we denote by

$${\rho }_{A,\ell }:\mathrm{Gal}\left(\overline{\mathbb{Q}}/\mathbb{Q}\right)\to {\mathrm{GSp}}_{2g}({\mathbb{Z}}_{\ell })$$

the |$\ell$|-adic representation, that is, the representation of |$\operatorname{Gal}(\overline{\mathbb Q}/\mathbb Q)$| on the |$\ell$|-adic Tate module |${\displaystyle \lim_\leftarrow A[\ell^n}]$|⁠.

For each prime |$p \nmid N_A$|⁠, we consider the |$p$|-Weil polynomial |$ P_{A, p}(X) $| of |$A$|⁠, which is uniquely determined by the property that

$$P_{A,p}(X)=\det \left(X{I}_{2g}-{\rho }_{A,\ell }\left({\mathrm{Frob}}_p\right)\right)$$

(2)

for any prime |$\ell \neq p$|⁠. In particular, we have

$$P_{A,p}(X)\equiv \det \left(X{I}_{2g}-{\overline{\rho }}_{A,m}\left({\mathrm{Frob}}_p\right)\right)(\mathrm{mod}m)$$

(3)

for any integer |$m$| coprime to |$p$|⁠. We write

$$P_{A,p}(X)=X^{2g}+a_{1,p}{X}^{2g-1}+\cdots +a_{g,p}{X}^g+p{a}_{g-1,p}{X}^{g-1}+\cdots +p^{g-1}{a}_{1,p}X+p^g\in \mathbb{Z}[X],$$

where the integers |$a_{i, p}$|⁠, |$1 \leq i \leq g-1$|⁠, are independent of |$\ell$|⁠.

For any integer |$t \in \mathbb Z$|⁠, we consider the function

$${\pi }_A(x,t):=\#\left\{p\le x:p\nmid N_A,a_{1,p}=t\right\}.$$

The reason we usually impose the restriction that our abelian varieties be principally polarized is for ease of notation. When the abelian variety is principally polarized, the image of the |$\ell$|-adic representation |$\rho_{A, \ell}$| lies in |$\operatorname{GSp}_{2g}(\mathbb Z_{\ell})$|⁠. Without the restriction on the polarization, the image lies in a group that can be defined by replacing the matrix |$J_{2g}$| of Section 2.1 below with a matrix that has a more complicated description, and our results could be modified accordingly; see, for example, Section 2.3 of [43] for the group of symplectic similitudes in this general setting.

 

Theorem 1.

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$| and let |$t \in \mathbb Z$|⁠. Assume that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠. Define

$$\alpha :=\frac{1}{2g^2+g+1},\beta :=\{\begin{array}{cc}\frac{1}{3}& \text{if\hspace{0.5em}g\hspace{0.5em}=\hspace{0.5em}1,}\\ \frac{1}{2g^2-g+3}& \text{ifg}\ge \text{2},\end{array}\gamma :=\{\begin{array}{cc}\frac{1}{2}& \text{if\hspace{0.5em}g\hspace{0.5em}=\hspace{0.5em}1,}\\ \frac{1}{8}& \text{if\hspace{0.5em}g\hspace{0.5em}=\hspace{0.5em}2,}\\ \frac{1}{2g^2-g+1}& \text{ifg}\ge \text{3}.\end{array}$$

For any |$\varepsilon > 0$| we have:

• (i1) unconditionally,

  $${\pi }_A(x,t){\ll }_{A,\epsilon }\frac{x}{{(\log x)}^{1+\alpha -\epsilon }};$$
• (i2) under GRH,

  $${\pi }_A(x,t){\ll }_{A,\epsilon }{x}^{1-\frac{\alpha }{2}+\epsilon };$$

• (ii) if |$t \neq \pm 2g$|⁠, then (i1) and (i2) hold with |$\alpha$| replaced by |$\beta$|⁠;

• (iii) if |$t = 0$|⁠,then (i1) and (i2) hold with |$\alpha$| replaced by |$\gamma$|⁠.

□

We will actually prove a more general result, stated as Theorem 14 in Section 4, and that the case |$g =1$| of Theorem 1 is [42, Theorem 20, p. 189].

An immediate consequence of Theorem 1 concerns the non-lacunarity of the sequence |$(a_{1, p})_p$|⁠:

 

Corollary 2.

We keep the setting and notation of Theorem 1. For any |$\varepsilon > 0$| we have:

• (i) unconditionally,

  $$\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge {(\log p)}^{\alpha -\epsilon }\right\}~\pi (x);$$
• (ii) under GRH,

  $$\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge p^{\frac{\alpha }{2}-\epsilon }\right\}~\pi (x).$$

Recall that |$\nu(n)$| denotes the number of distinct prime factors of a positive integer |$n$| and that an arithmetic function |$f(\cdot)$| is said to have normal order |$F(\cdot)$| if for all |$\varepsilon > 0$|⁠, then |$ (1 - \varepsilon) F(n) < f(n) < (1 + \varepsilon) F(n) $| for all but a zero density subset of positive integers |$n$|⁠. It is a classical result of Erdös, originating in work of Hardy and Ramanujan [25], that |$\nu(p-1)$| has normal order |$\log \log p$|⁠. More generally, Erdös and Kac [20] proved that |$\nu(p-1)$| has a normal distribution. Variations of these results have also been obtained in arithmetic geometric contexts, including that of modular forms [36]. We now prove such results in the context of abelian varieties:

 

Theorem 3.

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$|⁠. Assume that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠. Under GRH we have that, for any |$\tau \in \mathbb R$|⁠,

$$\underset{x\to \infty }{\lim }\frac{\#\left\{p\le x:p\nmid N_A,a_{1,p}\ne 0,\nu (a_{1,p})\le \log \log p+\tau \sqrt{\log \log p}\right\}}{\pi (x)}=\frac{1}{\sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{\tau }{\int }}{e}^{-\frac{t^2}{2}}}\text{\hspace{0.5em}d}t.$$

(4)

□

In particular, |$\nu(a_{1, p})$| has normal order |$\log \log p$|⁠.

The case |$g = 1$| not only recovers but also generalizes the main theorem of [36] for weight 2 newforms that are not of CM type.

Finally, in Conjecture 4 below we propose a generalization of (1) to the case of higher-dimensional abelian varieties for which |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| and for which the following holds:

Equidistribution assumption: the normalized traces |$\frac{ a_{1, p}}{\sqrt{p}}$| are equidistributed on |$[-2g, 2g]$| with respect to the projection by the trace map of the (normalized) Haar measure of the unitary symplectic group |$\operatorname{USp}(2g)$|⁠.

The assumption that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| gives rise to an integer |$m_A \geq 1$| that is the smallest positive integer |$m$| such that

$${\rho }_A(\mathrm{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}))={\Pi }^{-1}(\Im {\overline{\rho }}_{A,m}),$$

with |$ \Pi : \operatorname{GSp}_{2 g}(\hat{\mathbb Z}) \longrightarrow \operatorname{GSp}_{2 g}(\mathbb Z/m \mathbb Z)$| the natural projection.

The Equidistribution Assumption gives rise to a continuous function |$ \Phi : [-1, 1] \longrightarrow [0, \infty), $| nonzero at |$0$|⁠, with the property that for every interval |$I \subseteq [-1, 1]$| we have

$$\underset{x\to \infty }{\lim }\frac{\#\left\{p\le x:p\nmid N_A,\frac{a_{1,p}}{2g\sqrt{p}}\in I\right\}}{\pi (x)}={\displaystyle \underset{I}{\int }\Phi }(t)\text{\hspace{0.5em}d}t.$$

We propose:

 

Conjecture 4.

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$| and let |$t \in \mathbb Z$|⁠, |$t \neq 0$|⁠. Assume that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| and that the Equidistribution Assumption holds. Then, as |$x \rightarrow \infty$|⁠,

$${\pi }_A(x,t)~c(A,t)\frac{\sqrt{x}}{\log x},$$

where

$$\begin{array}{lll}\text{c(A,\hspace{0.5em}t)}\hfill & =\hfill & \frac{\Phi (0)}{g}\cdot \frac{m_{A,t}|C(m_{A,t},t)|}{\left|\Im {\overline{\rho }}_{A,m_{A,t}}\right|}\cdot \hfill \\ \hfill & \times \hfill & {\displaystyle \prod _{\ell \nmid m_A}\frac{{\ell }^{v_{\ell }(t)+1}\left|\right\{M\in {\mathrm{GSp}}_{2g}(\mathbb{Z}/{\ell }^{v_{\ell }(t)+1}\mathbb{Z}):\mathrm{tr}M\equiv t(\mathrm{mod}{\ell }^{v_{\ell }(t)+1})\left\}\right|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/{\ell }^{v_{\ell }(t)+1}\mathbb{Z})|}},\hfill \end{array}$$

the integers |$v_{\ell}(t) \geq 0$| are defined by |$\ell^{v_{\ell}(t)} | t$|⁠, |$ \ell^{v_{\ell}(t) + 1} \nmid t$|⁠, and

$$\begin{array}{c}{m}_{A,t}:=m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}},\\ C(m_{A,t},t):=\left\{M\in \Im {\overline{\rho }}_{A,m_{A,t}}:\mathrm{tr}M\equiv t(\mathrm{mod}{m}_{A,t})\right\}.\end{array}$$

If |$c(A, t) = 0$|⁠, we interpret the asymptotic as saying that there are at most finitely many primes |$p$| such that |$a_{1, p} = t$|⁠.

For a discussion about the possible growth of |$\pi_A(x, 0)$|⁠, see Section 5.

 

Remark 5.

The image of |$\rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| for a large class of abelian varieties. Indeed, in [43, 44] Serre showed that this holds whenever |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| and the dimension |$g$| of |$A$| is |$1$|⁠, |$2$|⁠, |$6$|⁠, or an odd number. An open image result also holds when |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$| and there exists a number field |$K$| such that the Néron model of |$A/K$| over the ring of integers of |$K$| has a semistable fibre of toric dimension 1; see [24]. As pointed out in [24, p. 704], for |$g \geq 2$| the image of |$\rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| for most abelian |$g$|-folds that arise as Jacobians of hyperelliptic curves defined by |$y^2 = f(x)$| with the degree |$n$| of the monic polynomial |$f \in \mathbb Z[x]$| equal to |$2 g + 1$| or |$2 g + 2$|⁠. Specifically, the hypotheses in Hall’s Theorem are satisfied if the Galois group of |$f$| is |$S_n$|⁠, or if there exists a rational prime |$p$| for which |$f (\mod p)$| has |$n-1$| distinct zeroes over an algebraic closure, one of which is a double zero; see Kowalski’s appendix in [24] and Zarhin’s article [50]. □

 

Remark 6.

When |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠, the Equidistribution Assumption is a very special case of a general conjecture explained in Section 13 of [45, Conjecture 13.5] that generalizes the Sato-Tate Conjecture. See also [15, pp. 173–174, 797–804, 906] and [40]. □

 

Remark 7.

Generalizations of the Lang-Trotter Conjecture (1) have been previously considered by other authors. For example, in [39], V. K. Murty addressed generalizations in the setting of modular forms, while in [28, pp. 421–423], Katz addressed generalizations in the setting of abelian varieties arising as Jacobians of genus |$g$| curves. Our conjecture encompasses a generic class of abelian varieties |$A$| and is precise in terms of both the growth in |$x$| and the constant depending on |$A$| and |$t$|⁠. The potential vanishing of the constant |$c(A, t)$| is an important open problem in itself. In [28, p. 420], for instance, Katz discusses a general mechanism that leads to congruence obstructions for realizing |$a_{1, p} = t$|⁠. We relegate this study to future work. □

The paper is structured as follows. In Section 2 we present some of the key results needed for proving Theorem 1, Corollary 2, and Theorem 3, and for arguing towards Conjecture 4. In Section 3 we prove Theorem 1 and Corollary 2 using the strategy of [42, Sections 7–8] and also with the help of the main result of Serre’s Appendix 1 of this aricle. In Section 4 we prove Theorem 3 following a general strategy of [5]. In Section 5 we provide our heuristic reasoning towards Conjecture 4 and address some connections with existing works. In Section 6 we provide computational data related to our theoretical investigations. J-P. Serre supplied two appendices: the first gives a result on the dimension of conjugacy classes in symplectic groups, while the second gives properties of a certain density function for unitary symplectic groups.

2 Generalities

2.1 Basic notation

Along with the standard analytic notation |$\operatorname{O}, \; \ll, \; \gg, \; \text{o}, \; \sim, $|

$$\begin{array}{l}\pi (x):=\#\{p\le x:p\text{\hspace{0.5em}prime}\},\\ \mathrm{li}x:={\displaystyle \underset{2}{\overset{x}{\int }}\frac{1}{\log t}}\text{\hspace{0.5em}d}t,\end{array}$$

we use |$p$| and |$\ell$| to denote rational primes; we write |$n | m^{\infty}$| to mean that all the prime divisors of |$n$| occur among the prime divisors of |$m$|⁠, possibly with higher multiplicities; we write |$n || m$| to mean that |$n | m$|⁠, but |$n^2 \nmid m$|⁠; we write |$v_{\ell}(n)$| for the valuation of |$n$| at |$\ell$|⁠.

For a commutative, unitary ring |$R$| and a positive integer |$g$|⁠, we denote by |$R^{\times}$| its group of units, by |$I_{g} \in M_{g}(R)$|⁠, |$I_{2g} \in M_{2g}(R)$| the identity matrices, and by

$$J_{2g}:=\left(\begin{array}{cc}0& I_g\\ -I_g& 0\end{array}\right)\in M_{2g}(R).$$

We recall that the general symplectic group on |$R$| is defined by

$${\mathrm{GSp}}_{2g}(R):=\left\{M\in {\mathrm{GL}}_{2g}(R):M^{\text{t}}{J}_{2g}M=\mu J_{2g}\text{\hspace{0.5em}\hspace{0.5em}for\hspace{0.5em}some\hspace{0.5em}}\mu \in R^{\times }\right\},$$

where |$M^{\text{t}}$| denotes the transpose of |$M$|⁠, while

$${\mathrm{Sp}}_{2g}(R):=\left\{M\in {\mathrm{GL}}_{2g}(R):M^{\text{t}}{J}_{2g}M=J_{2g}\right\}.$$

We note that |$\operatorname{GSp}_{2}(R) = \operatorname{GL}_2(R)$|⁠. We recall that |$\operatorname{GSp}_{2g}(R)$| has centre |$\{\mu I_{2g} : \mu \in R^{\times} \}$| and that, as an algebraic group, it has dimension |$2g^2 + g+1$|⁠.

For |$R = \mathbb C$|⁠, we recall that the unitary symplectic group is defined by

$$\mathrm{USp}(2g):=\left\{M\in {\mathrm{Sp}}_{2g}(ℂ):{\overline{M}}^{\text{t}}M=M{\overline{M}}^{\text{t}}=I_{2g}\right\}.$$

2.2 The Chebotarev density theorem

2.2.1 Finite extensions of a number field

Let |$L/K$| be a finite Galois extension of number fields and let |$G$| be its Galois group. Let |$C$| be a non-empty subset of |$G$| that is stable under conjugation. For any |$x > 0$|⁠, let

$${\pi }_C(x,L/K):=\#\{\mathfrak{p}\text{\hspace{0.5em}a\hspace{0.5em}place\hspace{0.5em}of\hspace{0.5em}K,\hspace{0.5em}unramified\hspace{0.5em}in\hspace{0.5em}L/K}:N_{K/\mathbb{Q}}(\mathfrak{p})\le x,{\mathrm{Frob}}_{\mathfrak{p}}\subseteq C\}.$$

The Chebotarev Density Theorem states that

$${\pi }_C(x,L/K)~\frac{\left|C\right|}{\left|G\right|}\pi (x).$$

We will use the following conditional effective version of this theorem:

 

Theorem 8.

([34]; for this version see [42, Theorem 4, p. 133]) Keep the above setting and notation. Assume GRH for the Dedekind zeta function of |$L$|⁠. Then there exists an absolute constant |$c > 0$| such that

$$\left|{\pi }_C(x,L/K)-\frac{\left|C\right|}{\left|G\right|}\pi (x)\right|\le c\frac{\left|C\right|}{\left|G\right|}{x}^{\frac{1}{2}}\left(\log |\mathrm{disc}(L/\mathbb{Q})|+|L:\mathbb{Q}|\log x\right).$$

□

In order to apply this theorem, the following variation of a result of Hensel [26], proved in [42], is useful:

 

Proposition 9.

([42, Theorem 4, p. 133]) Keep the above setting and notation. Then

$$\log \left|N_{K/\mathbb{Q}}(\mathrm{disc}(L/K))\right|\le (|L:\mathbb{Q}|-|K:\mathbb{Q}|)\left({\displaystyle \sum _{p\in P(L/K)}\log }p\right)+|L:\mathbb{Q}|\log |L:K|,$$

where

$$P(L/K):=\{\text{primes\hspace{0.5em}}p:\text{there is a place\hspace{0.5em}}\mathfrak{p}\hspace{0.5em}\text{of\hspace{0.5em}}K,\text{ramified in\hspace{0.5em}}L/K,\text{with\hspace{0.5em}}\mathfrak{p}\text{|p}\}.$$

□

2.2.2 |$\ell$|-adic extensions of a number field

In [42], Serre used the effective versions of the Chebotarev Density Theorem of Lagarias and Odlyzko [34] to deduce upper bounds for |$\pi_C(x, L/K)$| in the case of an |$\ell$|-adic Galois extension |$L/K$| of a number field |$K$|⁠. We recall his main results below.

Let |$K$| be a number field. Let |$\ell$| be a rational prime and |$G$| a compact |$\ell$|-adic Lie group of dimension |$D$|⁠. Denote by |$Z(G)$| the centre of |$G$|⁠. Let |$C \subseteq G$| be a non-empty closed subset of |$G$| that is stable under conjugation. In [42, Section 3] Serre explains what it means for the Minkowski dimension|$\dim_{\mathcal{M}} C$| of |$C$| to be |$\le d$|⁠. Let |$L/K$| be an infinite Galois extension, with Galois group |$G$|⁠. For any |$x > 0$|⁠, let

$${\pi }_C(x,L/K):=\#\{\mathfrak{p}\text{\hspace{0.5em}a\hspace{0.5em}place\hspace{0.5em}of\hspace{0.5em}}K\text{,\hspace{0.5em}unramified\hspace{0.5em}in\hspace{0.5em}}L/K:N_{K/\mathbb{Q}}(\mathfrak{p})\le x,{\mathrm{Frob}}_{\mathfrak{p}}\subseteq C\}.$$

Following [42, p. 151], we define

$$ϵ(x):=\frac{\log x}{{(\log \log x)}^2(\log \log \log x)}\text{\hspace{1em}and\hspace{1em}}{ϵ}_R(x):=\frac{x^{\frac{1}{2}}}{{(\log x)}^2}.$$

 

Theorem 10.

([42, Theorem 10, p. 151]) Keep the above setting and notation. Let |$0 \leq d < D$| be such that the Minkowski dimension of |$C$| satisfies |$ \dim_{\cal{M}} C \leq d. $| Define |$ \displaystyle{\alpha := \frac{D - d}{D}.} $|

• (i) Unconditionally, we have

  $${\pi }_C(x,L/K){\ll }_{K,L,C}\frac{\mathrm{li}x}{ϵ{(x)}^{\alpha }}.$$
  In particular, for any |$\varepsilon > 0$|⁠, we have

  $${\pi }_C(x,L/K){\ll }_{K,L,C,\epsilon }\frac{x}{{(\log x)}^{1+\alpha -\epsilon }}.$$
• (ii) Under GRH for Dedekind zeta functions, we have

  $${\pi }_C(x,L/K){\ll }_{K,L,C}\frac{\mathrm{li}x}{{ϵ}_R{(x)}^{\alpha }}.$$
  In particular, for any |$\varepsilon > 0$|⁠, we have

  $${\pi }_C(x,L/K){\ll }_{K,L,C,\epsilon }{x}^{1-\frac{\alpha }{2}+\epsilon }.$$

□

Serre obtains the following improvement in special cases:

 

Theorem 11.

([42, Theorem 12, p. 157]) Keep the above setting and notation. Let |$0 \leq d < D$| be such that the Minkowski dimension of |$C$| satisfies |$ \dim_{\cal{M}} C \leq d. $| Define

$$r_C:=\underset{M\in C}{\inf }\dim \frac{G}{Z_G(M)},$$

where |$Z_G(M)$| denotes the centralizer of |$M$| in |$G$|⁠. Define

$${\beta }_C:=\frac{D-d}{D-\frac{r_C}{2}}.$$

Then |$(i)$| and |$(ii)$| of Theorem 10 hold with |$\beta_C$| in place of |$\alpha$|⁠. □

Note that |$r_C \geq 0$|⁠, hence |$\beta_C \geq \alpha$| and so Theorem 11 is Theorem 10 when |$\beta_C = \alpha$|⁠. When |$r_C \geq 1$|⁠, hence |$\beta_C > \alpha$|⁠, Theorem 11 improves upon Theorem 10. This happens when |$C \cap Z(G) = \emptyset$|⁠.

2.3 Abelian varieties

Let |$A/\mathbb Q$| be an abelian variety of dimension |$g$| and let |$p$| be a prime of good reduction. Recall that for any root |$\pi \in \mathbb C$| of |$P_{A, p}(X)$| we have |$|\pi| = \sqrt{p}$|⁠, hence

$$\left|a_{1,p}\right|<2g\sqrt{p}.$$

(5)

Property (2) links the |$p$|-Weil polynomial |$P_{A, p}(X)$| to the division fields of |$A$|⁠, in particular to the Galois representation defining |$\rho_{A}$|⁠.

For arbitrary integers |$m \geq 1$| and |$t$|⁠, we set

$$\begin{array}{lll}\text{G(m)}\hfill & \text{:=}\hfill & \Im {\overline{\rho }}_{A,m},\hfill \\ \text{C(m,\hspace{0.5em}t)}\hfill & \text{:=}\hfill & \{M\in G(m):\mathrm{tr}M\equiv t(\mathrm{mod}m)\}.\hfill \end{array}$$

We recall that:

• by the Néron-Ogg-Shafarevich criterion,

  $$\text{the\hspace{0.5em}extension\hspace{0.5em}}\mathbb{Q}(A[m])\text{/}\mathbb{Q}\text{\hspace{0.5em}isunramified\hspace{0.5em}outside\hspace{0.5em}}m{N}_A;$$

  (6)
• by the injectivity of the restriction of |$\bar{\rho}_{A, m}$| to |${\operatorname{Gal}(\mathbb Q(A[m])/\mathbb Q)}$|⁠,

  $$|G(m)|\le |{\mathrm{GSp}}_{2g}(\mathbb{Z}/m\mathbb{Z})|\le m^{2g^2+g+1}.$$

  (7)

In many cases, the image of the representation |$\rho_{A}$| is better understood. For example, as already mentioned in Remark 5 of Section 1, for several classes of abelian varieties |$A/\mathbb Q$| with a trivial endomorphism ring, |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g} (\hat{\mathbb Z})$|⁠. In particular, for such |$A$| we have that:

• |$ \Im \rho_{A, \ell}$| is open in |$\operatorname{GSp}_{2 g}(\mathbb Z_{\ell})$| for all rational primes |$\ell$|⁠;

• |$G(\ell) \simeq \operatorname{GSp}_{2 g}(\mathbb Z/\ell \mathbb Z)$| for all but finitely many rational primes |$\ell$|⁠.

Lemma 12 below gives further consequences of the openness of |$\Im \rho_A$| in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠. To state the lemma, we introduce the following notation:

$$F_t(m):=\frac{m|C(m,t)|}{|G(m)|},H_t(m):=\frac{m\left|\right\{M\in {\mathrm{GSp}}_{2g}(\mathbb{Z}/m\mathbb{Z}):\mathrm{tr}M\equiv t(\mathrm{mod}m)\left\}\right|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/m\mathbb{Z})|};$$

for a sequence |$(s_n)_n$|⁠,

$$\underset{m\tilde{\to }\infty }{\lim }{s}_m:=\underset{n\to \infty }{\lim }{s}_{m_n}\text{\hspace{0.5em}\hspace{0.5em}with\hspace{0.5em}\hspace{0.5em}}{m}_n:={\displaystyle \prod _{\ell \le n}{\ell }^n}.$$

 

Lemma 12.

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$| such that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠.

• (i) There exists an integer |$m \geq 1$| such that |$\rho_A(\operatorname{Gal}(\overline{\mathbb Q}/\mathbb Q)) = \Pi^{-1}(G(m))$|⁠, where we recall that

  $$\Pi :{\mathrm{GSp}}_{2g}(\widehat{\mathbb{Z}})\to {\mathrm{GSp}}_{2g}(\mathbb{Z}/m\mathbb{Z})$$

  is the natural projection. Denote by |$m_A$| the least such integer.
• (ii) For all positive integers |$m_1, m_2$| with |$m_1 | m_A^{\infty} \; \; \text{and} \; \; (m_2, m_A) = 1,$| we have

  $$G(m_1{m}_2)\simeq G(m_1)\times G(m_2)=G(m_1)\times {\mathrm{GSp}}_{2g}(\mathbb{Z}/m_2\mathbb{Z}).$$
• (iii) For all |$t \in \mathbb Z$| we have

  $${\displaystyle \prod _{\ell }{H}_t}(\ell )<\infty .$$
  In particular, if |$t \neq 0$|⁠, then

  $${\displaystyle \prod _{\ell \nmid m_A}{H}_t}\left({\ell }^{v_{\ell }(t)+1}\right)<\infty .$$
• (iv) For all |$t \in \mathbb Z$|⁠, |$t \neq 0$|⁠, we have

  $$\underset{m\tilde{\to }\infty }{\lim }{F}_t(m)=F_t\left(m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}\right)\cdot {\displaystyle \prod _{\ell \nmid m_A}{H}_t}\left({\ell }^{v_{\ell }(t)+1}\right).$$

 

proof.

Parts (i) and (ii) are clear from the openness assumption on |$\Im \rho_A$|⁠. For part (iii), let |$\ell \nmid m_A$| and |$t$| be fixed. First, we will show that

$$\frac{\ell ℂ(\ell ,t)|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}=1+\mathrm{O}\left(\frac{1}{\ell }\right).$$

(8)

Recall that the multiplicator of |$\operatorname{GSp}_{2g}(\mathbb Z /\ell \mathbb Z)$| is the character of |$\operatorname{GSp}_{2g}(\mathbb Z /\ell \mathbb Z)$| with kernel |$\operatorname{Sp}_{2g}(\mathbb Z /\ell \mathbb Z)$|⁠; we denote it by |$\text{mult}$|⁠. Let |$\operatorname{char} (M)$| denote the characteristic polynomial of a square matrix |$M$|⁠. For |$\gamma \in (\mathbb Z / \ell \mathbb Z)^{\times}$|⁠, define

$$\begin{array}{lll}{\mathrm{GSp}}_{2g}{(\mathbb{Z}/\ell \mathbb{Z})}^{\gamma }\hfill & :=\hfill & {\text{mult}}^{-1}(\gamma ),\hfill \\ C{(\ell ,t)}^{\gamma }\hfill & :=\hfill & C(\ell ,t)\cap {\mathrm{GSp}}_{2g}{(\mathbb{Z}/\ell \mathbb{Z})}^{\gamma },\hfill \\ \mathcal{G}{(\ell )}^{\gamma }\hfill & :=\hfill & \left\{\mathrm{char}(M):M\in {\mathrm{GSp}}_{2g}{(\mathbb{Z}/\ell \mathbb{Z})}^{\gamma }\right\},\hfill \\ \mathcal{C}{(\ell ,t)}^{\gamma }\hfill & :=\hfill & \left\{M\in \mathcal{G}{(\ell )}^{\gamma }:\mathrm{tr}M=t\right\}.\hfill \end{array}$$

By [1, Lemma 2.4, p. 631],

$${\left(\frac{\ell }{\ell +1}\right)}^{2g^2+g}\frac{\left|\mathcal{C}{(\ell ,t)}^{\gamma }\right|}{\left|\mathcal{G}{(\ell )}^{\gamma }\right|}\le \frac{\left|C{(\ell ,t)}^{\gamma }\right|}{|{\mathrm{Sp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}\le {\left(\frac{\ell }{\ell -1}\right)}^{2g^2+g}\frac{\left|\mathcal{C}{(\ell ,t)}^{\gamma }\right|}{\left|\mathcal{G}{(\ell )}^{\gamma }\right|}.$$

Noting that |$|{\mathcal{C}}(\ell, t)^{\gamma}|= \ell^{g-1} $| and |$|{\mathcal{G}}(\ell)^{\gamma}| = \ell^g$|⁠, we deduce that

$${\left(\frac{\ell }{\ell +1}\right)}^{2g^2+g}\cdot \frac{1}{\ell }\le \frac{\left|C{(\ell ,t)}^{\gamma }\right|}{|{\mathrm{Sp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}\le {\left(\frac{\ell }{\ell -1}\right)}^{2g^2+g}\cdot \frac{1}{\ell }.$$

Combining the above inequalities for all |$\gamma \in (\mathbb Z / \ell \mathbb Z)^{\times}$| and multiplying by |$\ell$| gives

$${\left(\frac{\ell }{\ell +1}\right)}^{2g^2+g}\le \frac{\ell |C(\ell ,t)|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}\le {\left(\frac{\ell }{\ell -1}\right)}^{2g^2+g}.$$

This completes the proof of (8).

Next we will prove that

$$\frac{\ell |C(\ell ,t)|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}=1+\mathrm{O}\left(\frac{1}{{\ell }^2}\right).$$

(9)

This ensures the convergence of the infinite product |$\displaystyle\prod_{\ell} H_t(\ell)$|⁠, proving (iii).

We first prove (9) for |$t \neq 0$|⁠. For this, observe that for any |$t_1$|⁠, |$t_2 \in \mathbb Z$| we have

$$t_1\equiv t_2(\mathrm{mod}\ell )\Rightarrow C(\ell ,t_1)=C(\ell ,t_2)$$

and

$$t_1\cancel{\equiv }0(\mathrm{mod}\ell ),t_2\cancel{\equiv }0(\mathrm{mod}\ell )\Rightarrow |C(\ell ,t_1)|=|C(\ell ,t_2)|.$$

Indeed, the first assertion is trivial, while the second assertion follows by noting that, if |$t_1 \not\equiv 0 (\mod \ell)$| and |$t_2 \not\equiv 0 (\mod \ell)$|⁠, then the endomorphism |$\left[t_2 t_1^{-1}\right]$| of |$\operatorname{GSp}_{2g}(\mathbb Z/\ell \mathbb Z)$| defined by multiplication by |$t_2 t_1^{-1}$| is a bijection satisfying that |$\left[t_2 t_1^{-1}\right] (C(\ell, t_1)) = C(\ell, t_2)$|⁠.

From the above observations,

$$|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|=|C(\ell ,0)|+(\ell -1)|C(\ell ,t)|.$$

It is now easy to show that (9) follows from this along with (8) for |$|C(\ell, 0)|$|⁠.

Now we prove (9) for |$t = 0$|⁠. When |$g =1$|⁠, a straightforward calculation gives that

$$|C(\ell ,0)|={\ell }^3-{\ell }^2$$

and so

$$\frac{\ell |C(\ell ,0)|}{|{\mathrm{GL}}_2(\mathbb{Z}/\ell \mathbb{Z})|}=\frac{{\ell }^3(\ell -1)}{\ell (\ell -1)({\ell }^2-1)}=\frac{{\ell }^2}{{\ell }^2-1}=1+\mathrm{O}\left(\frac{1}{{\ell }^2}\right).$$

When |$g \geq 2$|⁠, we proceed as follows. By [32, Theorem 5.3, p. 170],

$$|C(\ell ,t)|=g(\ell )+\{\begin{array}{ll}-{\ell }^{-1}f(\ell )\hfill & \text{if\hspace{0.5em}}t\ne 0,\hfill \\ {\ell }^{-1}(\ell -1)f(\ell )\hfill & \text{if\hspace{0.5em}}t=0,\hfill \end{array}$$

(10)

for some explicit polynomials |$f(\ell)$| and |$g(\ell)$| in |$\ell$|⁠. Of relevance to us is that the degree |$d_{g(\ell)}$| of the leading term of |$g(\ell)$| in |$\ell$| satisfies

$$d_{g(\ell )}=2g^2+g,$$

(11)

and that the degree |$d_{f(\ell)}$| of the leading term of |$f(\ell)$| in |$\ell$|⁠, while less explicit, can be shown to satisfy

$$d_{f(\ell )}\le \frac{3g^2}{2}+\frac{g}{2}+1.$$

(12)

Before justifying this bound, let us complete the proof of (9) for |$t = 0$|⁠, |$g \geq 2$|⁠. From (9), we see that for any |$t \neq 0$|⁠,

$$|C(\ell ,0)|=f(\ell )+|C(\ell ,t)|.$$

Since we already know (9) for |$t \neq 0$|⁠, it suffices to show that

$$\frac{\ell f(\ell )}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}=\mathrm{O}\left(\frac{1}{{\ell }^2}\right).$$

This follows from (11) and (12), as well as the assumption that |$g \geq 2$|⁠; indeed,

$$d_{g(\ell )}-d_{f(\ell )}\ge \frac{g^2}{2}+\frac{g}{2}-1\ge 2.$$

Consequently, (9) holds for |$t=0$|⁠, |$g \geq 2$|⁠.

Finally, let us justify (12). The expression for |$f(\ell)$| is rather delicate; indeed, Kim showed that

$$\begin{array}{ll}f(\ell )\hfill & ={\ell }^{g^2-1}{\displaystyle \sum _{b=0}^{�g/2�}{\ell }^{b(b+1)}}{\displaystyle \prod _{m=0}^{2b-1}\frac{({\ell }^{g-m}-1)}{({\ell }^{2b-m}-1)}}{\displaystyle \prod _{j=1}^b({\ell }^{2j-1}-1)}{\displaystyle \sum _{k=1}^{�(g-2b+2)/2�}{\ell }^k}\hfill \\ \hfill & \times {\displaystyle \sum _{\alpha \in {\mathbb{F}}_{\ell }^{\times }}K}{(\alpha )}^{g-2b+2-2k}{\displaystyle \sum _{\begin{array}{c}{j}_1,\dots ,j_{k-1}\\ 2k-1\le j_{k-1}\le \cdots \le j_1\le g-2b+1\end{array}}{\displaystyle \prod _{v=1}^{k-1}({\ell }^{j_v-2v}-1)}},\hfill \end{array}$$

(13)

where |$K(\alpha)$| is the ordinary Kloosterman sum

$$K(\alpha )=K(\lambda ;\alpha ,1):={\displaystyle \sum _{a\in {\mathbb{F}}_q^{\times }}\lambda }(a\alpha +a^{-1})$$

for any non-trivial additive character |$\lambda$| of |$\mathbb F_q$|⁠.

To find the leading term, we first focus on

$${\displaystyle \sum _{\alpha \in {\mathbb{F}}_{\ell }^{\times }}K}{(\alpha )}^r$$

for an arbitrary integer |$r \geq 0$|⁠.

When |$r = 0$|⁠, the sum is simply |$\ell-1$|⁠. When |$r=1$|⁠, by Weil’s estimate on Kloosterman sums |$\left| K(\alpha) \right| \le 2\sqrt{\ell}$|⁠, we deduce that |$\left|\sum_{\alpha \in \mathbb F_\ell^\times} K(\alpha)\right| \leq \ell^2$|⁠. When |$r \geq 2$|⁠, Kim remarks that

$${\displaystyle \sum _{\alpha \in {\mathbb{F}}_{\ell }^{\times }}K}{(\alpha )}^r={\ell }^2{M}_{r-1}-{(\ell -1)}^{r-1}+2{(-1)}^{r-1},$$

where |$M_0 := 1$| and for any integer |$s \geq 1$|⁠,

$$M_s:=\left|\left\{({\alpha }_1,\dots {\alpha }_s)\in {({\mathbb{F}}_{\ell }^{\times })}^s:{\alpha }_1+\dots +{\alpha }_s=1\text{\hspace{0.5em}and\hspace{0.5em}}{\alpha }_1^{-1}+\cdots +{\alpha }_s^{-1}=1\right\}\right|.$$

Note that |$M_1 = 1$| and that for |$s \ge 2$|⁠, the first of the two conditions defining |$M_s$| gives |$\alpha_1$| linearly in terms of the other |$\alpha_i$|⁠, while the second gives |$\alpha_2$| as a root of a quadratic in the remaining terms. Thus, if |$s \geq 2$|⁠, then |$M_{s} \leq 2(\ell-1)^{s-2}$|⁠. It follows that when |$r=2$|⁠, the sum |$\sum_{\alpha \in \mathbb F_\ell^\times} K(\alpha)^r$| is bounded by an expression of leading degree at most |$2$| in |$\ell$| (by direct computation using |$M_1$|⁠), and when |$r \ge 3$|⁠, by an expression of leading degree at most |$r-1$| in |$\ell$|⁠.

Using the above estimates, we now focus on the degree |$d_{f(\ell)}$| of the leading term in (13) we deduce that

$$\begin{array}{c}{d}_{f(\ell )}\le \max \{g^2+2bg-2b^2+b+k+kg-2bk-k^2+1:0\le b\le \lfloor \frac{g}{2}\rfloor ,\\ 1\le k\le \lfloor \frac{g-2b+2}{2}\rfloor \}.\end{array}$$

The quadratic function above is maximized when |$b = \lfloor \frac{g}{2} \rfloor$| and |$k = \lfloor \frac{g-2b+2}{2} \rfloor =1$|⁠, with maximal value |$\frac{3g^2}{2} + \frac{g}{2} + 1$|⁠; the bound (12) follows. This proves (9), and therefore the first part of (iii).

To prove the second part of (iii), observe that |$t \neq 0$| is divisible by at most finitely many primes, and so |$\displaystyle\prod_{\ell \nmid m_A} H_t \left( \ell^{v_{\ell}(t) + 1} \right)$| is a constant multiple of |$\displaystyle\prod_{ \ell} H_t(\ell)$|⁠, hence finite by the first part of (iii).

Now we prove (iv). Fix an arbitrary |$t \in \mathbb Z$| with |$t \neq 0$|⁠. For now, fix also a positive integer |$m$| such that |$(m, m_A) = 1$| or |$m_A |m$|⁠, and a prime divisor |$\ell$| of |$m$|⁠. Write |$m = m_0\ell^{v_{\ell}(m)}$|⁠, |$t = t_0 \ell^{v_{\ell}(t)}$|⁠, where |$m_0, t_0 \in \mathbb Z$| satisfy |$\ell \nmid m_0$|⁠, |$\ell \nmid t_0$|⁠, and note that |$v_{\ell} (m) \geq 1$|⁠. For any |$s \in \mathbb Z$| such that |$s \equiv t (\mod m \ell^{v_{\ell}(t)})$|⁠, we have |$v_{\ell}(s) = v_{\ell}(t)$| since |$v_{\ell}(m) \ge 1$|⁠. Therefore we may write |$ s = s_0\ell^{v_{\ell}(t)} $| with |$s_0 \in \mathbb Z$| and |$\ell \nmid s_0$|⁠. By the Chinese Remainder Lemma, there exists |$u \in \mathbb Z$| such that |$u \equiv t_0^{-1}s_0 \left(\mod \ell \right)$| and |$u \equiv 1 (\mod m_0)$|⁠, hence such that

$$\begin{array}{ll}ut\hfill & \equiv s\left(\mathrm{mod}{\ell }^{v_{\ell }(t)+1}\right),\hfill \end{array}$$

(14)

$$\begin{array}{ll}u\hfill & \equiv 1(\mathrm{mod}m).\hfill \end{array}$$

(15)

We have

$$u{I}_{2g}\in G(m),$$

(16)

since if |$(m, m_A) = 1$| then by (ii) we have |$G(m) = \operatorname{GSp}_{2 g} (\mathbb Z/m \mathbb Z)$| and so |$u I_{2 g} \in G(m)$|⁠, while if |$m _A| m$| then |$ u \equiv 1 (\mod m_A) $| (by (15)) and

$$\left\{M\in {\mathrm{GSp}}_{2g}\left(\widehat{\mathbb{Z}}\right):M\equiv 1(\mathrm{mod}{m}_A)\right\}\subseteq \Im {\rho }_A$$

(by the definition of |$m_A$|⁠) and thus |$u I_{2 g} \in G(m)$|⁠.

Using (14) and (16), we deduce that the multiplication by |$u I_{2g}$| map

$$\begin{array}{l}\begin{array}{lll}C\left(m{\ell }^{v_{\ell }(t)+1},t\right)\hfill & \to \hfill & C\left(m{\ell }^{v_{\ell }(t)+1},s\right)\hfill \\ M\hfill & \mapsto \hfill & u{I}_{2g}M\hfill \end{array}\\ \end{array}$$

is a bijection; in particular,

$$\left|C\left(m{\ell }^{v_{\ell }(t)+1},s\right)\right|=\left|C\left(m{\ell }^{v_{\ell }(t)+1},t\right)\right|.$$

(17)

Now consider the natural projection

$$\Pi :G\left(m{\ell }^{v_{\ell }(t)+1}\right)\to G\left(m{\ell }^{v_{\ell }(t)}\right)$$

and observe that

$$\left|{\Pi }^{-1}(I_{2g})\right|\cdot \left|G\left(m{\ell }^{v_{\ell }(t)}\right)\right|=\left|G\left(m{\ell }^{v_{\ell }(t)+1}\right)\right|.$$

(18)

Letting

$$S:=\left\{s\left(\mathrm{mod}m{\ell }^{v_{\ell }(t)}\right):s\equiv t\left(\mathrm{mod}m{\ell }^{v_{\ell }(t)}\right)\right\},$$

and using (17), we obtain

$$\begin{array}{lll}\left|{\Pi }^{-1}(I_{2g})\right|\cdot \left|C\left(m{\ell }^{v_{\ell }(t)},t\right)\right|\hfill & =\hfill & \left|{\Pi }^{-1}\left(C\left(m{\ell }^{v_{\ell }(t)},t\right)\right)\right|\hfill \\ \hfill & =\hfill & \left|{\displaystyle \underset{s\left(\mathrm{mod}m{\ell }^{v_{\ell }(t)}\right)\in S}{\cup }C}\left(m{\ell }^{v_{\ell }(t)+1},s\right)\right|\hfill \\ \hfill & =\hfill & \left|S\right|\cdot \left|C\left(m{\ell }^{v_{\ell }(t)+1},t\right)\right|\hfill \\ \hfill & =\hfill & \ell \cdot \left|C\left(m{\ell }^{v_{\ell }(t)+1},t\right)\right|,\hfill \end{array}$$

giving

$$\left|{\Pi }^{-1}(I_{2g})\right|\cdot \left|C\left(m{\ell }^{v_{\ell }(t)},t\right)\right|=\ell \cdot \left|C\left(m{\ell }^{v_{\ell }(t)+1},t\right)\right|.$$

(19)

Putting together (18) and (19), we deduce that for all positive integers |$m$| such that |$(m, m_A) = 1$| or |$m_A |m$|⁠, and for all primes |$\ell\mid m$|⁠, we have

$$F_t\left(m{\ell }^{v_{\ell }(t)+1}\right)=F_t\left(m{\ell }^{v_{\ell }(t)}\right)$$

and thus

$$F_t\left(m{\ell }^k\right)=F_t\left(m{\ell }^{v_{\ell }(t)}\right)\text{\hspace{1em}for\hspace{0.5em}all\hspace{0.5em}k}\ge {\text{v}}_{\ell }(\text{t}).$$

Therefore for all $d \mid m_A$ we have

$$F_t\left(d{m}_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}\right)=F_t\left(m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}\right)$$

(20)

and for all |$k \geq 1$| and all primes |$\ell \nmid m_A$| we have

$$F_t\left({\ell }^{v_{\ell }(t)+k}\right)=F_t\left({\ell }^{v_{\ell }(t)+1}\right).$$

(21)

Now for any positive integer |$m$| consider its unique factorization

$$m=m_1\cdot m_2,\text{\hspace{0.5em}with\hspace{0.5em}}{m}_1|m_A^{\infty }\text{\hspace{0.5em}and\hspace{0.5em}}(m_{\text{2}},m_A)\text{=1}.$$

By (ii),

$$F_t(m)=F_t(m_1){\displaystyle \prod _{\ell |m_2}{H}_t}\left({\ell }^{v_{\ell }(m_2)}\right).$$

Using (20) for the second line below and (21) for the third line, we have

$$\begin{array}{lll}\underset{m\tilde{\to }\infty }{\lim }{F}_t(m)\hfill & =\hfill & \underset{m\tilde{\to }\infty }{\lim }{F}_t(m_1){\displaystyle \prod _{\ell |m_2}{H}_t}\left({\ell }^{v_{\ell }(m_2)}\right)\hfill \\ \hfill & =\hfill & F_t\left(m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}\right)\cdot \underset{x\to \infty }{\lim }{\displaystyle \prod _{\begin{array}{c}\ell <x\\ \ell \nmid m_A\end{array}}}\underset{n\to \infty }{\lim }{H}_t\left({\ell }^n\right)\hfill \\ \hfill & =\hfill & F_t\left(m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}\right)\cdot {\displaystyle \prod _{\ell \nmid m_A}{H}_t}\left({\ell }^{v_{\ell }(t)+1}\right),\hfill \end{array}$$

which gives (iv). ∎

 

Remark 13.

As in the case |$g =1$|⁠, when |$g = 2$| it is possible to derive closed formulae for the quotient |$\frac{|C(\ell, t)|}{|\operatorname{GSp}_{4}(\mathbb Z/\ell \mathbb Z)|}$|⁠; indeed, we have

$$|{\mathrm{GSp}}_4(\mathbb{Z}/\ell \mathbb{Z})|={\ell }^4(\ell -1)({\ell }^2-1)({\ell }^4-1)$$

and

$$|C(\ell ,t)|=\{\begin{array}{ll}{\ell }^5(\ell -1)({\ell }^4-\ell -1)\hfill & \text{\hspace{0.5em}if\hspace{0.5em}}t=0,\hfill \\ {\ell }^4({\ell }^6-{\ell }^5-{\ell }^4+\ell +1)\hfill & \text{\hspace{0.5em}if\hspace{0.5em}}t\ne 0.\hfill \end{array}$$

(22)

We sketch a proof of the latter using arguments from [8]; we leave it as an exercise to the reader to derive these formulae using the aforementioned results of [32]. We will use these formulae in Remark 24.

Define

$$N_{\ell ,t}:=\left|\left\{(x,y,\delta )\in {({(\mathbb{Z}/\ell \mathbb{Z})}^{\times })}^3:y\ne -\delta ,\left(x+\frac{y}{x}\right)\left(1+\frac{\delta }{y}\right)=t\right\}\right|.$$

It follows from the proof of [8, Theorem 12] that

$$\left|\left\{M\in {\mathrm{GSp}}_4(\mathbb{Z}/\ell \mathbb{Z}):\mathrm{tr}M\equiv t(\mathrm{mod}\ell )\right\}\right|$$

equals

$$\begin{array}{l}{\ell }^4\left({(\ell -1)}^2(\ell -2)+N_{\ell ,t}\right)+{\ell }^4(\ell -1){({\ell }^2-1)}^2+{\ell }^5{(\ell -1)}^2({\ell }^3-\ell -1)\\ +\{\begin{array}{cc}({\ell }^7-{\ell }^4)(\ell -1)& \text{\hspace{0.5em}if\hspace{0.5em}}t=0,\\ 0& \text{\hspace{0.5em}if\hspace{0.5em}}t\ne 0.\end{array}\end{array}$$

We will now show that

$$N_{\ell ,t}=\{\begin{array}{cc}(\ell -1)(\ell -2)& \text{\hspace{0.5em}if\hspace{0.5em}}t=0,\\ {(\ell -2)}^2& \text{\hspace{0.5em}if\hspace{0.5em}}t\ne 0,\end{array}$$

which in turn confirms (22).

Note that

$$\left|\left\{(x,y,\delta )\in {({(\mathbb{Z}/\ell \mathbb{Z})}^{\times })}^3:y\ne -\delta \right\}\right|={(\ell -1)}^2(\ell -2)$$

and

$$N_{\ell ,0}=\left|\left\{(x,y,\delta )\in {({(\mathbb{Z}/\ell \mathbb{Z})}^{\times })}^3:y\ne -\delta ,\left(x+\frac{y}{x}\right)\left(1+\frac{\delta }{y}\right)=0\right\}\right|=(\ell -1)(\ell -2),$$

since, for any given |$x$|⁠, the defining conditions of these sets determine |$y$| uniquely, provided that |$\delta \neq -y$|⁠. Putting the two together, we obtain that

$$\left|\left\{(x,y,\delta )\in {({(\mathbb{Z}/\ell \mathbb{Z})}^{\times })}^3:y\ne -\delta ,\left(x+\frac{y}{x}\right)\left(1+\frac{\delta }{y}\right)\ne 0\right\}\right|=(\ell -1){(\ell -2)}^2.$$

Dividing by |$\ell-1$|⁠, we deduce that |$N_{\ell,t} = (\ell-2)^2$| for any fixed nonzero |$t$|⁠; this completes the proof of (22). □

3 Proof of Theorem 1

For a prime |$\ell$| and an integer |$t$|⁠, define:

$$\begin{array}{lll}{\mathbb{G}}_{\ell }\hfill & :=\hfill & {\mathrm{GSp}}_{2g}({\mathbb{Z}}_{\ell });\hfill \\ P{\mathbb{G}}_{\ell }\hfill & :=\hfill & {\mathbb{G}}_{\ell }/Z({\mathbb{G}}_{\ell });\hfill \\ \Pi :{\mathbb{G}}_{\ell }\hfill & \to \hfill & P{\mathbb{G}}_{\ell }\text{\hspace{0.5em}the\hspace{0.5em}canonical\hspace{0.5em}projection};\hfill \\ G_{\ell }\hfill & :=\hfill & \mathrm{Im}{\rho }_{A,\ell };\hfill \\ {G^{\prime }}_{\ell }\hfill & :=\hfill & \Pi (G_{\ell });\hfill \\ {ℂ}_{\ell }(t)\hfill & :=\hfill & \left\{M\in {\mathbb{G}}_{\ell }:\mathrm{tr}M=t\right\};\hfill \\ C_{\ell }(t)\hfill & :=\hfill & \left\{M\in G_{\ell }:\mathrm{tr}M=t\right\};\hfill \\ {C^{\prime }}_{\ell }(0)\hfill & :=\hfill & \Pi \left(C_{\ell }(0)\right);\hfill \\ r_{C_{\ell }(t)}\hfill & :=\hfill & \underset{M\in C_{\ell }(t)}{\inf }\dim \frac{G_{\ell }}{Z_{G_{\ell }}(M)};\hfill \\ r_{{C^{\prime }}_{\ell }(t)}\hfill & :=\hfill & \underset{M\in {C^{\prime }}_{\ell }(0)}{\inf }\dim \frac{{G^{\prime }}_{\ell }}{Z_{{G^{\prime }}_{\ell }}(M)}.\hfill \end{array}$$

We will deduce Theorem 1 from the following more general result:

 

Theorem 14.

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$| and let |$t \in \mathbb Z$|⁠.

• (i) Assume that there exists a prime |$\ell$| such that:

  • (a) |$G_\ell$| is open in |$\mathbb G_\ell$|⁠;

  • (b) |$\exists \; 0 \leq d < \dim \mathbb G_{\ell} \; \text{such that} \; \dim_{{\cal{M}}} C_{\ell}(t) \leq d.$|

  Define

  $$\alpha :=\frac{\dim {\mathbb{G}}_{\ell }-d}{\dim {\mathbb{G}}_{\ell }}.$$

Then for any |$\varepsilon > 0$| we have:

• (i1) unconditionally,

  $${\pi }_A(x,t){\ll }_{A,\ell ,\epsilon }\frac{x}{{(\log x)}^{1+\alpha -\epsilon }};$$

  (23)
• (i2) under GRH,

  $${\pi }_A(x,t){\ll }_{A,\ell ,\epsilon }{x}^{1-\frac{\alpha }{2}+\epsilon }.$$

  (24)

• (ii) If |$t \neq \pm 2g$|⁠, assume that there exists a prime |$\ell$| such that:

  • (a) |$G_\ell$| is open in |$\mathbb G_\ell$|⁠;

  • (b) |$\exists \; 0 \leq d < \dim \mathbb G_{\ell} \; \text{such that} \; \dim_{{\cal{M}}} C_{\ell}(t) \leq d;$|

  • (c) |$v_\ell(\frac{t}{2g}) \neq 0$|⁠.

  Define

  $$\beta :=\frac{\dim {\mathbb{G}}_{\ell }-d}{\dim {\mathbb{G}}_{\ell }-\frac{r_{C_{\ell }(t)}}{2}}.$$

  Then |$r_{C_{\ell}(t)} > 0$| and the equations (23) and (24) hold with |$\alpha$| replaced by |$\beta$|⁠.

• (iii) If |$t=0$|⁠, assume that there exists a prime |$\ell$| such that:

  • (a) |$G_\ell$| is open in |$\mathbb G_\ell$|⁠;

  • (b) |$ \exists \; 0 \leq d < \dim P\mathbb G_{\ell} \; \text{such that} \; \dim_{{\cal{M}}} C'_{\ell}(0) \leq d.$|

  Define

  $$\gamma :=\frac{\dim {\mathbb{G}}_{\ell }-1-d}{\dim {\mathbb{G}}_{\ell }-1-\frac{r_{{C^{\prime }}_{\ell }(0)}}{2}}.$$

  Then |$r_{C'_{\ell}(0)} > 0$| and the equations (23) and (24) hold with |$\alpha$| replaced by |$\gamma$|⁠.\qedhere

□

 

proof.

Throughout the proof we let |$x > 0$|⁠, to be thought of as approaching |$\infty$|⁠.

(i) Observe that, by (2), for any rational prime |$\ell$| we have

$${\pi }_A(x,t)\le {\pi }_{C_{\ell }(t)}(x,L/\mathbb{Q}),$$

where

$$L:={\overline{\mathbb{Q}}}^{\mathrm{Ker}{\rho }_{A,\ell }}.$$

It remains to estimate |$\pi_{C_{\ell}(t)}(x, L/\mathbb Q)$|⁠, which we do by following the method of [42, Section 8].

We choose |$\ell$| as in the hypothesis of (i). Since |$G_\ell$| is open in |$\mathbb G_\ell$|⁠, we have |$\dim G_{\ell} = \dim \mathbb G_{\ell}$|⁠. We apply Theorem 10 to the extension |$L/\mathbb Q$| and the conjugacy set |$C_{\ell}(t)$| with |$D := \dim \mathbb G_{\ell}$|⁠.

(ii) If |$t \neq \pm 2g$|⁠, we choose |$\ell$| as in the hypothesis of (ii). As before, |$\dim G_{\ell} = \dim \mathbb G_{\ell}$|⁠. Moreover,

$${ℂ}_{\ell }(t)\cap Z({\mathbb{G}}_{\ell })=\varnothing ,$$

for, otherwise, recalling that |$ Z(\mathbb G_\ell) = \{\mu I_{2 g}: \mu \in \mathbb Z_{\ell}^{\times}\}, $| we would have that the |$\ell$|-adic valuation of |$\frac{t}{2g}$| satisfies |$v_{\ell}\left(\frac{t}{2 g}\right) = 0$|⁠, a contradiction.

In particular, for any |$M \in \mathbb C_{\ell}(t)$|⁠,

$$Z_{{\mathbb{G}}_{\ell }}(M)⊊{\mathbb{G}}_{\ell }.$$

(25)

Centralizers are closed subgroups, hence Lie subgroups, and |$Z_{\mathbb G_\ell}(M)$| has a well-defined dimension. Since |$\operatorname{GSp}_{2g}$| is connected as an algebraic group, (25) implies that

$$\dim Z_{{\mathbb{G}}_{\ell }}(M)<\dim {\mathbb{G}}_{\ell }=\dim G_{\ell }.$$

If |$M \in C_{\ell}(t)$|⁠, then |$\dim Z_{G_{\ell}}(M) \leq \dim Z_{\mathbb G_{\ell}}(M)$| and, by the above,

$$\dim \frac{G_{\ell }}{Z_{G_{\ell }}(M)}\ge \dim {\mathbb{G}}_{\ell }-\dim Z_{{\mathbb{G}}_{\ell }}(M)\ge 1.$$

Therefore we can improve upon the result of (i) by applying Theorem 11 to the extension |$L/\mathbb Q$| and the conjugacy set |$C_{\ell}(t)$| with |$D := \dim \mathbb G_{\ell}$|⁠.

(iii) If |$t = 0$|⁠, we choose |$\ell$| as in the hypothesis of (iii) and with |$\hat{\rho}_{A, \ell} := \Pi \circ \rho_{A, \ell}$| we consider

$$L^{\prime }:={\overline{\mathbb{Q}}}^{\mathrm{Ker}{\widehat{\rho }}_{A,\ell }},$$

a Galois extension of |$\mathbb Q$| with Galois group |$G'_{\ell}$|⁠. Observing that

$${\pi }_A(x,0)\le {\pi }_{{C^{\prime }}_{\ell }(0)}(x,L^{\prime }/\mathbb{Q}),$$

it remains to estimate the right-hand side.

Since |$G_\ell$| is open in |$\mathbb G_\ell$|⁠, we have that |$G'_\ell$| is open in |$P\mathbb G_\ell$| and so |$\dim G'_{\ell} = \dim P\mathbb G_\ell = \dim \mathbb G_{\ell} - 1$|⁠. Moreover, since |$Z(P\mathbb G_\ell) = \{I_{2g}\}$|⁠, we have

$$\Pi ({ℂ}_{\ell }(0))\cap Z(P{\mathbb{G}}_{\ell })=\varnothing .$$

In particular, as in the proof of part (ii), for any |$M \in \mathbb C_{\ell}(0)$|⁠,

$$Z_{P{\mathbb{G}}_{\ell }}(\Pi (M))⊊P{\mathbb{G}}_{\ell },$$

thus

$$\dim Z_{P{\mathbb{G}}_{\ell }}(\Pi (M))<\dim {\mathbb{G}}_{\ell }-1.$$

If |$M \in C_{\ell}(0)$|⁠, then |$\dim Z_{G'_{\ell}}(\Pi(M)) \leq \dim Z_{P\mathbb G_{\ell}}(\Pi(M))$| and, by the above,

$$\dim \frac{{G^{\prime }}_{\ell }}{Z_{{G^{\prime }}_{\ell }}(\Pi (M))}\ge \dim P{\mathbb{G}}_{\ell }-\dim Z_{P{\mathbb{G}}_{\ell }}(\Pi (M))\ge 1.$$

Therefore we can improve upon the result of (i) by applying Theorem 11 to the extension |$L'/\mathbb Q$| and the conjugacy set |$C'_{\ell}(0)$| with |$D := \dim \mathbb G_{\ell} - 1$|⁠. ∎

 

Proof of Theorem 1.

In our setting, by the openness assumption on |$\Im \rho_A$|⁠, hypothesis (a) of Theorem 14 holds for any prime |$\ell$|⁠. It remains to verify hypothesis (b) and to compute the values of |$\alpha$|⁠, |$\beta$|⁠, and |$\gamma$|⁠.

To verify hypothesis (b) of either parts (i) or (ii), observe that |$\mathbb C_{\ell}(t)$| is a closed subvariety of the algebraic group |$\operatorname{GSp}_{2g}$| and so |$C_\ell(t)$| has a well-defined dimension strictly smaller than |$\dim \mathbb G_\ell$|⁠. The bound applies to the Minkowski dimension |$\dim_{\mathcal{M}}C_\ell(t)$| also by [42, Theorem 8]. Part (b) follows with |$d := \dim \mathbb G_\ell - 1$|⁠.

To verify hypothesis (b) of part (iii), observe that |$\Pi(\mathbb C_{\ell}(0))$| is a closed subvariety of the algebraic group |$P\mathbb G_{\ell}$| and so |$C'_{\ell}(0)$| has a well-defined dimension strictly smaller than |$\dim P\mathbb G_\ell$|⁠. The bound applies to the Minkowski dimension |$\dim_{\mathcal{M}}C'_\ell(0)$| also by [42, Theorem 8]. Part (b) follows with |$d := \dim \mathbb G_\ell - 2$|⁠.

Recalling that |$\dim \operatorname{GSp}_{2g} = 2g^2 + g + 1$|⁠, we see that |$\alpha = \frac{1}{2 g^2 + g + 1}$|⁠.

If |$g=1$|⁠, then |$r_{C_{\ell}}(t)$| and |$r_{C'_{\ell}}(0)$| are calculated as in [42, pp. 189–190], giving rise to |$\beta = \frac{1}{3}$| and |$\gamma = \frac{1}{2}$|⁠. If |$g \geq 2$|⁠, then |$r_{C_{\ell}}(t)$| and |$r_{C'_{\ell}}(0)$| are estimated using Serre’s Theorem A.1 in Appendix 1. Indeed, by this theorem and Remark 5 that follows its statement, for |$M \in C_{\ell}(t)$| with |$t$| as in (ii) we have

$$r_{C_{\ell }(t)}=\underset{M\in C_{\ell }(t)}{\inf }\dim \frac{G_{\ell }}{Z_{G_{\ell }}(M)}=\underset{M\in {ℂ}_{\ell }(t)}{\inf }\dim \frac{{\mathbb{G}}_{\ell }}{Z_{{\mathbb{G}}_{\ell }}(M)}\ge 4g-4,$$

which gives

$$\beta \ge \frac{1}{2g^2-g+3}.$$

To improve upon this bound when |$t = 0$|⁠, we focus on estimating |$\gamma$| and use

$$\dim Z_{P{\mathbb{G}}_{\ell }}\left(\Pi (M)\right)=\dim Z_{{\mathbb{G}}_{\ell }}(M)-1.$$

(26)

If |$g =2$|⁠, we use (26) and once again the first part of Theorem A.1 in Appendix 1 to deduce

$$\gamma \ge \frac{1}{(2g^2+g+1)-1-\frac{4g-4}{2}}=\frac{1}{8}.$$

If |$g \geq 3$|⁠, we use (26) and the last part of Theorem A.1 in Appendix 1 to deduce

$$\gamma \ge \frac{1}{(2g^2+g+1)-1-\frac{4g-2}{2}}=\frac{1}{2g^2-g+1}.$$

This completes the proof of Theorem 1. ∎

 

Proof of Corollary 2

The proof of Corollary 2 is deduced easily from part (i) of Theorem 1 and the Prime Number Theorem, as follows. Unconditionally,

$$\begin{array}{lll}\pi (x)\hfill & =\hfill & \begin{array}{l}\#\{p\le x:p|N_A\}+\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge {(\log p)}^{\alpha -\epsilon }\right\}\\ +\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|<{(\log p)}^{\alpha -\epsilon }\right\}\end{array}\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge {(\log p)}^{\alpha -\epsilon }\right\}+{\mathrm{O}}_A(1)+\mathrm{O}\left({\displaystyle \sum _{\begin{array}{c}t\in \mathbb{Z}\\ \left|t\right|<{(\log x)}^{\alpha -\epsilon }\end{array}}{\pi }_A}(x,t)\right)\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge {(\log p)}^{\alpha -\epsilon }\right\}+{\mathrm{O}}_A(1)+{\mathrm{O}}_{A,\epsilon }\left(\frac{x}{{(\log x)}^{1+\alpha -\frac{\epsilon }{2}}}\cdot {(\log x)}^{\alpha -\epsilon }\right)\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge {(\log p)}^{\alpha -\epsilon }\right\}+\text{o}\left(\pi (x)\right).\hfill \end{array}$$

Under GRH,

$$\begin{array}{lll}\pi (x)\hfill & =\hfill & \#\{p\le x:p|N_A\}+\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge p^{\frac{\alpha }{2}-\epsilon }\right\}+\#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|<p^{\frac{\alpha }{2}-\epsilon }\right\}\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge p^{\frac{\alpha }{2}-\epsilon }\right\}+{\mathrm{O}}_A(1)+\mathrm{O}\left({\displaystyle \sum _{\begin{array}{c}t\in \mathbb{Z}\\ \left|t\right|<x^{\frac{\alpha }{2}-\epsilon }\end{array}}{\pi }_A}(x,t)\right)\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge p^{\frac{\alpha }{2}-\epsilon }\right\}+{\mathrm{O}}_A(1)+{\mathrm{O}}_{A,\epsilon }\left(x^{1-\frac{\alpha }{2}+\frac{\epsilon }{2}}\cdot x^{\frac{\alpha }{2}-\epsilon }\right)\hfill \\ \hfill & =\hfill & \#\left\{p\le x:p\nmid N_A,\left|a_{1,p}\right|\ge p^{\frac{\alpha }{2}-\epsilon }\right\}+\text{o}\left(\pi (x)\right).\hfill \end{array}$$

The uniformity in |$t$| of the bounds for |$\pi_A(x, t)$| provided by Theorem 1 was crucial in the above estimates. ∎

4 Proof of Theorem 3

Let |$A/\mathbb Q$| be a principally polarized abelian variety of dimension |$g$| such that |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$|⁠. We will investigate |$\nu(a_{1, p})$| via the method of moments, with the goal of proving:

 

Proposition 15.

Assume GRH. Then

$$\frac{1}{\pi (x)}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log x\right)}^k}=c_k{(\log \log x)}^{\frac{k}{2}}+\text{\hspace{0.5em}o}\left({(\log \log x)}^{\frac{k}{2}}\right)$$

(27)

for each integer |$k \geq 1$|⁠, where

$$c_k:=\{\begin{array}{cc}\frac{k!}{2^{\frac{k}{2}}\left(\frac{k}{2}\right)!}& \text{if\hspace{0.5em}}k\text{\hspace{0.5em}even}\\ 0& \text{if\hspace{0.5em}}k\text{\hspace{0.5em}odd}\end{array}$$

is the |$k$|th moment of the standard Gaussian. □

With this, by adapting to our context the proof of the Erdös-Kac Theorem due to Billingsley [5] (see also [4] and the references therein for an accessible exposition), Theorem 3 is proved.

The core ingredient in our proof is the following application of (6)–(7), Theorem 8 (under GRH) and Proposition 9: for any positive integer |$m$| and any |$x > 0$| (to be thought of as approaching infinity), we have

$${\pi }_{C(m,0)}(x,\mathbb{Q}(A[m])/\mathbb{Q})=\frac{|C(m,0)|}{|G(m)|}\pi (x)+\mathrm{O}\left(|C(m,0)|x^{\frac{1}{2}}\log (m{N}_{A}x)\right).$$

(28)

Related to this, remark that by the openness assumption of |$\Im \rho_A$| in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| and by (8) from the proof of part (iii) of Lemma 12, we have

$$\frac{|C(\ell ,0)|}{|G(\ell )|}=\frac{1}{\ell }+\mathrm{O}\left(\frac{1}{{\ell }^2}\right)$$

(29)

for all |$\ell \nmid m_A$|⁠. In particular, for any |$y > 0$|⁠,

$${\displaystyle \sum _{\ell \le y}\frac{|C(\ell ,0)|}{|G(\ell )|}}=\log \log y+{\mathrm{O}}_A(1),$$

(30)

and, after using (29) and (7),

$${\displaystyle \sum _{\ell \le y}|}C(\ell ,0)|\ll \frac{y^{2g^2+g+1}}{\log y}.$$

(31)

Crucial to the method is also the following simple observation. Let |$x> 0$| and |$0 < \delta < 1$| be fixed and let |$y := x^{\delta}$|⁠. For any integer |$m \geq 1$|⁠, we have

$$|\nu (m)-{\nu }_y(m)|\le \frac{\log m}{\delta \log x},$$

(32)

where |$\nu_y(m)$| denotes the number of distinct prime divisors |$\ell \leq y$| of |$m$|⁠.

We now proceed with the proof of (18). For each prime |$\ell$|⁠, we define a random variable |$R_{\ell}$| to be |$1$| with probability |$\frac{1}{\ell}$| and |$0$| with probability |$1 - \frac{1}{\ell}$|⁠. Upon taking |$y := x^{\delta}$| for some fixed |$0 < \delta < 1$| and |$x \rightarrow \infty$|⁠, |$ R(y) := \displaystyle\sum_{\ell \leq y} R_{\ell} $| becomes normally distributed with mean and variance each equal to |$\log \log x$|⁠; by the Central Limit Theorem, for any integer |$k \geq 1$| we have

$$\mathbb{E}\left({(R(y)-\log \log x)}^k\right)=c_k{(\log \log x)}^{\frac{k}{2}}+\text{o}\left({(\log \log x)}^{\frac{k}{2}}\right).$$

(33)

By (29), |$R_{\ell}$| models the event that |$\ell | a_{1, p}$| for some |$p$|⁠. Our strategy then is to prove (27) by comparing |$\mathbb E\left( (R(y) - \log \log x)^k \right)$| and |$ \frac{1}{\pi(x)} \displaystyle\sum_{ p \leq x \atop{ p \nmid N_A \atop{ a_{1, p} \neq 0 } } } (\nu_y(a_{1, p}) - \log \log x)^k $| for each |$k \geq 1$|⁠.

We fix |$x > 0$| and |$k \geq 1$|⁠, choose a parameter |$\delta = \delta(g, k)$| such that

$$0<\delta <\frac{1}{2k\left(2g^2+g+1\right)}$$

(34)

and define |$y := x^{\delta}$|⁠. In what follows, our |$\operatorname{O}$|-estimates will reflect the growth of various functions as |$x \rightarrow \infty$|⁠.

For each |$\ell$| and each |$p \nmid N_A$|⁠, we define

$${\delta }_{\ell }(p):=\{\begin{array}{ll}1\hfill & \text{if\hspace{0.5em}}\ell \text{|}{a}_{1,p},\hfill \\ 0\hfill & \text{else.}\hfill \end{array}$$

Then, for each integer |$1 \leq j \leq k$|⁠, upon applying (28)–(31) and (33), we obtain

$$\begin{array}{lll}\hfill & \hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\nu }_y}{(a_{1,p})}^j\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}}{\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}{\delta }_{{\ell }_1}}(p)\dots {\delta }_{{\ell }_j}(p)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}\#}\left\{p\le x:p\nmid N_A,a_{1,p}\ne 0,\mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\}|a_{1,p}\right\}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}\#}\left\{p\le x:p\nmid N_A,\mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\}|a_{1,p}\right\}+\mathrm{O}(\pi {(y)}^j{\pi }_A(x,0))\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}\#}\left\{p\le x:p\nmid \mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\}{N}_A,\mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\}|a_{1,p}\right\}\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}\#}\left\{p\le x:p\nmid N_A,p\left|\mathrm{lcm}\right\{{\ell }_1,\dots ,{\ell }_j\left\}\right|a_{1,p}\right\}+\mathrm{O}(\pi {(y)}^j{\pi }_A(x,0))\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\ell }_1,\dots ,{\ell }_j\le y}{\pi }_{C(\mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\},0)}}(x,\mathbb{Q}(A[\mathrm{lcm}\{{\ell }_1,\dots ,{\ell }_j\}])/\mathbb{Q})+\mathrm{O}\left(j\pi {(y)}^j\right)+\mathrm{O}\left({\pi }_A(x,0)\pi {(y)}^j\right)\hfill \\ \hfill & =\hfill & \mathbb{E}(R{(y)}^j)\pi (x)+{\mathrm{O}}_j\left(\pi (x){(\log \log y)}^{j-1}\right)+{\mathrm{O}}_{A,j}\left(\frac{y^{j(2g^2+g+1)}}{{(\log y)}^j}{x}^{\frac{1}{2}}\log x\right)+{\mathrm{O}}_j\left(\pi {(y)}^j{\pi }_A(x,0)\right).\hfill \end{array}$$

By the binomial theorem and the above, we deduce

$$\begin{array}{ll}\hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}({\nu }_y(}{a}_{1,p})-\log \log x{)}^k\hfill \\ \hfill & {\displaystyle \sum _{0\le j\le k}\left(\begin{array}{c}k\\ j\end{array}\right)}{(-\log \log x)}^{k-j}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\nu }_y}{(a_{1,p})}^j\hfill \\ \hfill & {\displaystyle \sum _{0\le j\le k}\left(\begin{array}{c}k\\ j\end{array}\right)}{(-\log \log x)}^{k-j}\mathbb{E}(R{(y)}^j)\pi (x)\hfill \\ \hfill & +{\mathrm{O}}_{A,k}\left(y^{k(2g^2+g+1)}{x}^{\frac{1}{2}}(\log x){(\log \log x)}^k\right)+{\mathrm{O}}_k\left(\pi {(y)}^k{\pi }_A(x,0){(\log \log x)}^k\right).\hfill \end{array}$$

Recalling the choice of |$\delta$| given in (34) and using part (i2) of Theorem 1, we see that the two |$\operatorname{O}$|-terms above become |$\operatorname{O}_{\varepsilon, A, k}\left( x^{1 - \varepsilon} (\log x) (\log \log x)^k \right)$|⁠, which is |$\text{o}\left(\pi(x) (\log \log x)^{\frac{k}{2}}\right)$|⁠. Then, upon applying the binomial theorem once again in order to rewrite the first term, we deduce

$$\frac{1}{\pi (x)}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}({\nu }_y(}{a}_{1,p})-\log \log x{)}^k~\mathbb{E}({(R(y)-\log \log x)}^k).$$

(35)

Finally, recalling (5) and (32) and applying (33) and (35) several times, we deduce

$$\begin{array}{lll}\frac{1}{\pi (x)}\hfill & \hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log x\right)}^k}\hfill \\ \hfill & =\hfill & \frac{1}{\pi (x)}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left({\nu }_y(a_{1,p})-\log \log x+\mathrm{O}\left(\frac{\log \left|a_{1,p}\right|}{\delta \log x}\right)\right)}^k}\hfill \\ \hfill & =\hfill & \frac{1}{\pi (x)}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left({\nu }_y(a_{1,p})-\log \log x\right)}^k}+{\mathrm{O}}_{k,g,\delta }\left({\displaystyle \sum _{0\le j\le k-1}\frac{1}{\pi (x)}}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left|{\nu }_y(a_{1,p})-\log \log x\right|}^j}\right)\hfill \\ \hfill & =\hfill & \frac{1}{\pi (x)}{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left({\nu }_y(a_{1,p})-\log \log x\right)}^k}+{\mathrm{O}}_k\left({(\log \log x)}^{\frac{k-1}{2}}\right)\hfill \\ \hfill & =\hfill & c_k{(\log \log x)}^{\frac{k}{2}}+\text{o}\left({(\log \log x)}^{\frac{k}{2}}\right).\hfill \end{array}$$

This completes the proof of Theorem 3.

 

Remark 16.

The first and second moments of |$\nu(a_{1, p})$| may be estimated directly, without any comparison with the model defined by |$R_{\ell}$|⁠. The strategy originates in Turán’s proof of the Hardy-Ramanujan Theorem, [47], and is summarized below. □

We choose |$0 < \delta < \frac{1}{8 g^2 + 4 g + 1}$| and let |$y = x^{\delta}$|⁠. Then, proceeding as in the proof of Theorem 3 but without the model |$R_{\ell}$|⁠, we obtain

$$\begin{array}{lll}\hfill & \hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log x\right)}^2}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}\nu }{(a_{1,p})}^2-2(\log \log x){\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}\nu }(a_{1,p})+{(\log \log x)}^2\#\{p\le x:p\nmid N_A,a_{1,p}\ne 0\}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left({\nu }_y(a_{1,p})+{\mathrm{O}}_A(1)\right)}^2}\hfill \\ \hfill & \hfill & -2(\log \log x){\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}\left({\nu }_y(a_{1,p})+{\mathrm{O}}_A(1)\right)}+\pi (x){(\log \log x)}^2+\mathrm{O}({\pi }_A(x,0){(\log \log x)}^2)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\nu }_y}{(a_{1,p})}^2-2(\log \log x){\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\nu }_y}(a_{1,p})+\pi (x){(\log \log x)}^2\hfill \\ \hfill & \hfill & +\mathrm{O}\left({\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\nu }_y}(a_{1,p})\right)+\mathrm{O}(\pi (x)\log \log x)+\mathrm{O}({\pi }_A(x,0){(\log \log x)}^2)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\begin{array}{c}{\ell }_1,{\ell }_2\le y\\ {\ell }_1\ne {\ell }_2\end{array}}\frac{|C({\ell }_1{\ell }_2,0)|}{|G({\ell }_1{\ell }_2)|}}\pi (x)+{\mathrm{O}}_A\left({\displaystyle \sum _{{\ell }_1,{\ell }_2\le y}|}C({\ell }_1{\ell }_2,0)|x^{\frac{1}{2}}\log x\right)-2(\log \log x){\displaystyle \sum _{\ell \le y}\frac{|C(\ell ,0)|}{|G(\ell )|}}\pi (x)\hfill \\ \hfill & \hfill & +{\mathrm{O}}_A\left({\displaystyle \sum _{\ell \le y}|}C(\ell ,0)|x^{\frac{1}{2}}(\log x)(\log \log x)\right)+\pi (x){(\log \log x)}^2+{\mathrm{O}}_A\left({\displaystyle \sum _{\ell \le y}\frac{|C(\ell ,0)|}{|G(\ell )|}}\pi (x)\right)\hfill \\ \hfill & \hfill & +{\mathrm{O}}_A\left({\displaystyle \sum _{\ell \le y}|}C(\ell ,0)|x^{\frac{1}{2}}\log x\right)+\mathrm{O}(\pi (x)\log \log x)+\mathrm{O}({\pi }_A(x,0){(\log \log x)}^2)\hfill \\ \hfill & =\hfill & \pi (x){(\log \log x)}^2+{\mathrm{O}}_A\left(\frac{x^{2\delta (2g^2+g+1)}}{\log x}{x}^{\frac{1}{2}}\right)-2\pi (x){(\log \log x)}^2\hfill \\ \hfill & \hfill & +\mathrm{O}\left(x^{\delta (2g^2+g+1)}{x}^{\frac{1}{2}}\log \log x\right)\hfill \\ \hfill & \hfill & +\pi (x){(\log \log x)}^2+{\mathrm{O}}_A\left(\pi (x)\log \log x\right)\hfill \\ \hfill & \hfill & +{\mathrm{O}}_A\left(x^{\delta (2g^2+g+1)}{x}^{\frac{1}{2}}\log x\right)+{\mathrm{O}}_A\left({\pi }_A(x,0){(\log \log x)}^2\right)\hfill \\ \hfill & =\hfill & {\mathrm{O}}_A\left(\pi (x)\log \log x\right).\hfill \end{array}$$

(36)

The cancellation of the |$\pi(x) (\log \log x)^2$| terms is essential and that the choice of |$\delta$| ensures that the largest emerging |$\operatorname{O}$|-term depending on |$y$|⁠, namely |$\operatorname{O}_{A}\left( \frac{ x^{2 \delta (2 g^2 + g + 1)} }{\log x} x^{\frac{1}{2}} \right)$|⁠, is sufficiently small; precisely, it is |$\ll_A \pi(x) \ll_A \pi(x) \log \log x$|⁠.

 

Remark 17.

That |$\nu(a_{1, p})$| has normal order |$\log \log p$| can be deduced easily from the second moment estimate (36). In particular, this is an immediate consequence of the following variation of (36):

$${\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log p\right)}^2}{\ll }_A\pi (x)\log \log x.$$

In turn, this is obtained by remarking that

$${\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log p\right)}^2}\ll {\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\nu (a_{1,p})-\log \log x\right)}^2}+{\displaystyle \sum _{\begin{array}{c}p\le x\\ \begin{array}{c}p\nmid N_A\\ a_{1,p}\ne 0\end{array}\end{array}}{\left(\log \frac{\log x}{\log p}\right)}^2},$$

using (36) for the first sum and splitting the last sum over |$p$| into a sum over |$p \leq \sqrt{x}$| and one over |$\sqrt{x} < p \leq x$|⁠, followed by elementary estimates. □

 

Remark 18.

The normal order of |$\nu(a_{1, p})$| may also be obtained via the ubiquitous large sieve; see [33, Proposition 2.15] for generalities related to such works. Moreover, the |$k$|th moments (27) may be estimated more precisely via sieve methods by applying the general result [23, Proposition 3]. □

5 Heuristic Reasoning for Conjecture 4

We devote this section to arguing heuristically towards Conjecture 4. Our main setting will be that of a principally polarized abelian variety |$A/\mathbb Q$| of dimension |$g$| for which |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| and which satisfies the Equidistribution Assumption. In particular, the function |$\Phi$| introduced in Section 1 is bounded, continuous, and nonzero on |$(-1, 1)$|⁠; this was proved in more than one way in email communication between Katz [29] and Serre; in Appendix 2 we include a letter from Serre to Katz that contains such a proof.

 

Definition 19.

For each integer |$m \geq 1$| and prime |$p$|⁠, define |$c_{p,m} \in (0, \infty)$| by

$$c_{p,m}=\frac{|G(m)|}{m{\displaystyle \sum _{\begin{array}{c}\tau \in \mathbb{Z}\\ \left|\tau \right|<2g\sqrt{p}\end{array}}\Phi }\left(\frac{\tau }{2g\sqrt{p}}\right)|C(m,\tau )|}$$

and define the function

$$\begin{array}{l}{f}_p^{(m)}:\mathbb{Z}\to [0,\infty ),\\ f_p^{(m)}(\tau ):=\{\begin{array}{cc}\Phi \left(\frac{\tau }{2g\sqrt{p}}\right)\cdot \frac{m|C(m,\tau )|}{|G(m)|}\cdot c_{p,m}& \text{if|}\tau \text{|}<\text{2g}\sqrt{\text{p}},\\ 0& \text{\hspace{0.5em}else.}\end{array}\end{array}$$

□

Note that

$${\displaystyle \sum _{\tau \in \mathbb{Z}}{f}_p^{(m)}}(\tau )=1.$$

 

Lemma 20.

For all integers |$m \geq 1$| and |$\tau_0 \in \mathbb Z$| we have

$$\underset{p\to \infty }{\lim }\frac{m}{2g\sqrt{p}}{\displaystyle \sum _{\begin{array}{c}\tau \in \mathbb{Z}\\ \begin{array}{c}\left|\tau \right|<2g\sqrt{p}\\ \tau \equiv {\tau }_0(\mathrm{mod}m)\end{array}\end{array}}\Phi }\left(\frac{\tau }{2g\sqrt{p}}\right)=1.$$

□

 

proof.

This follows by viewing the expression inside the limit as a Riemann sum approximation of the integral |$\displaystyle\int_{-1}^{1} \Phi (\tau) \; d \tau = 1$|⁠. For more details, see [35, pp. 31–32]. ∎

 

Lemma 21.

For all integers |$m \geq 1$| we have

$$\underset{p\to \infty }{\lim }2g\sqrt{p}{c}_{p,m}=1.$$

□

 

proof.

By the definition of |$c_{p, m}$| and Lemma 20,

$$\begin{array}{lll}\underset{p\to \infty }{\lim }\frac{1}{2g\sqrt{p}{c}_{p,m}}\hfill & =\hfill & \underset{p\to \infty }{\lim }\frac{1}{2g\sqrt{p}}{\displaystyle \sum _{{\tau }_0=0}^{m-1}}{\displaystyle \sum _{\begin{array}{c}\tau \in \mathbb{Z}\\ \begin{array}{c}\left|\tau \right|<2g\sqrt{p}\\ \tau \equiv {\tau }_0(\mathrm{mod}m)\end{array}\end{array}}\Phi }\left(\frac{\tau }{2g\sqrt{p}}\right)\frac{m|C(m,\tau )|}{|G(m)|}\hfill \\ \hfill & =\hfill & \underset{p\to \infty }{\lim }{\displaystyle \sum _{{\tau }_0=0}^{m-1}\frac{|C(m,{\tau }_0)|}{|G(m)|}}\left(\frac{m}{2g\sqrt{p}}{\displaystyle \sum _{\begin{array}{c}\tau \in \mathbb{Z}\\ \begin{array}{c}\left|\tau \right|<2g\sqrt{p}\\ \tau \equiv {\tau }_0(\mathrm{mod}m)\end{array}\end{array}}\Phi }\left(\frac{\tau }{2g\sqrt{p}}\right)\right)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\tau }_0=0}^{m-1}\frac{|C(m,{\tau }_0)|}{|G(m)|}}\hfill \\ \hfill & =\hfill & 1.\hfill \end{array}$$

∎

Now let us fix |$t \in \mathbb Z$| and assume that |$\displaystyle\lim_{m \; \widetilde{\rightarrow} \; \infty} f_p^{(m)}(t)$| models the likelihood of the event |$a_{1, p} = t$|⁠, as guided by the Chebotarev law for all |$m$|-division fields and by the behaviour of |$\frac{a_{1,p}}{2g\sqrt{p}}$| in the interval |$(-1,1)$|⁠. Then, recalling part (iv) of Lemmas 12 and 21, we reason heuristically as follows:

$$\begin{array}{lll}\#\{p\hfill & \le \hfill & x:p\nmid N_A,a_{1,p}=t\}\hfill \\ \hfill & \approx \hfill & \underset{m\tilde{\to }\infty }{\lim }{\displaystyle \sum _{p\le x}{f}_p^{(m)}}(t)\hfill \\ \hfill & =\hfill & \underset{m\tilde{\to }\infty }{\lim }{\displaystyle \sum _{p\le x}\Phi }\left(\frac{t}{2g\sqrt{p}}\right)\cdot \frac{m|C(m,t)|}{|G(m)|}\cdot c_{p,m}\hfill \\ \hfill & \approx \hfill & \left(\underset{m\tilde{\to }\infty }{\lim }\frac{m|C(m,t)|}{|G(m)|}\right){\displaystyle \sum _{p\le x}\Phi }\left(\frac{t}{2g\sqrt{p}}\right)\cdot \frac{1}{2g\sqrt{p}}\hfill \\ \hfill & =\hfill & \left(\underset{m\tilde{\to }\infty }{\lim }{F}_t(m)\right){\displaystyle \sum _{p\le x}\Phi }\left(\frac{t}{2g\sqrt{p}}\right)\cdot \frac{1}{2g\sqrt{p}}.\hfill \end{array}$$

Here, the symbol |$\approx$| means equality deduced purely heuristically. The last line is simply notation, as introduced in Section 2.2.

To understand the growth of the last sum, we use the properties of the function |$\Phi$|⁠. For any |$\varepsilon > 0$|⁠, by the continuity of |$\Phi$| at |$0$|⁠, there exists a |$\delta > 0$| such that

$$\left|\frac{t}{2g\sqrt{p}}\right|<\delta \Rightarrow \left|\Phi \left(\frac{t}{2g\sqrt{p}}\right)-\Phi (0)\right|<\epsilon .$$

(37)

We thus split the sum over |$p \leq x$| according to the above |$\delta$|-interval. By the boundedness of |$\Phi$|⁠, we obtain

$$\left|{\displaystyle \sum _{p<\frac{t^2}{4g^2{\delta }^2}}\left(\Phi \left(\frac{t}{2g\sqrt{p}}\right)-\Phi (0)\right)}\frac{1}{2\sqrt{p}}\right|{\ll }_{t,\epsilon ,g}1.$$

By (37) and by noting that |$\displaystyle\sum_{p \leq x} \frac{1}{2 \sqrt{p}} \sim \frac{\sqrt{x}}{\log x}$|⁠, we obtain

$$\left|{\displaystyle \sum _{\frac{t^2}{4g^2{\delta }^2}<p\le x}\left(\Phi \left(\frac{t}{2g\sqrt{p}}\right)-\Phi (0)\right)}\frac{1}{2\sqrt{p}}\right|\ll \frac{\epsilon \sqrt{x}}{\log x}.$$

Taking |$\varepsilon \rightarrow 0$| and returning to our heuristics, we are led to the possible prediction that

$$\#\{p\le x:p\nmid N_A,a_{1,p}=t\}~\frac{\Phi (0)}{g}\cdot \underset{m\tilde{\to }\infty }{\lim }{F}_t(m)\cdot \frac{\sqrt{x}}{\log x}.$$

(38)

When |$t \neq 0$|⁠, we proved in parts (iii) and (iv) of Lemma 12 that the limit over |$m \; \widetilde{\rightarrow} \; \infty$| exists and equals an infinite product; in this case, we conjecture that

$$\begin{array}{l}\#\{p\le x:p\nmid N_A,a_{1,p}=t\}~\\ \frac{\Phi (0)}{g}\cdot \frac{m_{A,t}|C(m_{A,t},t)|}{|G(m_{A,t})|}\cdot {\displaystyle \prod _{\ell \nmid m_A}\frac{{\ell }^{v_{\ell }(t)+1}\left|\right\{M\in {\mathrm{GSp}}_{2g}(\mathbb{Z}/{\ell }^{v_{\ell }(t)+1}\mathbb{Z}):\mathrm{tr}M\equiv t(\mathrm{mod}{\ell }^{v_{\ell }(t)+1})\left\}\right|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/{\ell }^{v_{\ell }(t)+1}\mathbb{Z})|}}\cdot \frac{\sqrt{x}}{\log x},\end{array}$$

(39)

where we recall

$$m_{A,t}=m_A{\displaystyle \prod _{\ell |m_A}{\ell }^{v_{\ell }(t)}}.$$

When |$t = 0$| and |$g = 1$|⁠, the limit over |$m \; \widetilde{\rightarrow} \; \infty$| exists and equals an infinite product by [35, Lemma 2, p. 34]; see Remark 22 below. When |$t = 0$| and |$g \geq 2$|⁠, we are currently unable to make a similar statement and relegate such a study to future work.

We conclude this section with several remarks about the above conjecture.

 

Remark 22.

Assume |$g = 1$| and |$\operatorname{End}_{\overline{\mathbb Q}}(E) \simeq \mathbb Z$|⁠. Then |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| (see [41]) and the Equidistribution Assumption holds (see [3, 11, 12]). In this case, |$\Phi(x) = \frac{2}{ \pi} \sqrt{1 - x^2}$| and (38) coincides with the formulation in (1) of the Lang-Trotter Conjecture on Frobenius traces of [35]. Combining this with the formula

$$|\mathbb{G}{L}_2(\mathbb{Z}/\ell \mathbb{Z})|=\ell (\ell -1)\left({\ell }^2-1\right)$$

and with [35, Lemma 2, p. 34], we obtain an equivalent reformulation of (38):

$${\pi }_A(x,t)~\frac{2}{\pi }\cdot \frac{m_A|C(m_A,t)|}{|G(m_A)|}\cdot {\displaystyle \prod _{\begin{array}{c}\ell \nmid m_A\\ \ell \mid t\end{array}}\frac{{\ell }^2}{{\ell }^2-1}}\cdot {\displaystyle \prod _{\ell \nmid t{m}_A}\frac{\ell \left({\ell }^2-\ell -1\right)}{(\ell +1){(\ell -1)}^2}}\cdot \frac{\sqrt{x}}{\log x}.$$

(40)

□

 

Remark 23.

Assume |$g=2$| and |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$|⁠. Then |$\Im \rho_A$| is open in |$\operatorname{GSp}_{2g}(\hat{\mathbb Z})$| ([43], [44]) and the Sato-Tate group of |$A$| is |$\operatorname{USp}(4)$| [21, Theorem 4.3], while the Equidistribution Assumption is an open question. The function |$\Phi(\cdot)$| may be calculated explicitly using the Weyl integration formula as in [31]. In particular, this calculation leads to the value

$$\Phi (0)=\frac{256}{15{\pi }^2}.$$

We explain the calculation of |$\Phi(0)$| here briefly. Let |$ L_p(A, T) := T^{4} P_{A, p} \left(\frac{1}{T}\right) $| be the |$p$|-Euler factor in the |$L$|-function of |$A$| and let |$ \bar{L}_p(A, T) = L_p\left(A, \frac{T}{\sqrt{p}}\right) $| be its normalization. Let

$$S:=\left\{(x_1,x_2)\in {ℝ}^2:x_2\ge 2x_1-2,x_2\ge -2x_1-2,x_2\le \frac{x_1^2}{4}+2\right\}$$

and let |$R(x_1)$| be the defining interval of |$x_2$| imposed by the constraints of |$S$|⁠. Recalling that the Sato-Tate group associated to |$A$| is |$\operatorname{USp}(4)$|⁠, the conjectured joint density function of the normalized coefficients |$\bar{a}_{1, p}$| and |$\bar{a}_{2, p}$| is

$$\frac{1}{4{\pi }^2}\sqrt{\max \{\rho ({\overline{a}}_{1,p},{\overline{a}}_{2,p}),0\}},$$

where

$$\rho (x_1,x_2):=\left(x_1^2-4x_2+8\right)\left(x_2-2x_1+2\right)\left(x_2+2x_1+2\right),$$

with support in the region |$S$| where |$\rho$| is non-negative. Consequently, for any interval |$I \subseteq [-4, 4]$|⁠, the set

$$\left\{p:{\overline{a}}_{1,p}\in I\right\}$$

is expected to have natural density

$${\displaystyle \underset{I}{\int }}{\displaystyle \underset{R(x_1)}{\int }\frac{1}{4{\pi }^2}}\sqrt{\max \{\rho (x_1,x_2),0\}}\text{\hspace{0.5em}d}{x}_2\text{\hspace{0.5em}d}{x}_1.$$

(For details, see the original source, specifically [21, p. 21 and p. 40].) Let

$$\Psi (x)=\frac{1}{4{\pi }^2}{\displaystyle \underset{R(x)}{\int }\sqrt{\max \{\rho (x,x_2),0\}}}\text{d}{x}_2.$$

In particular, |$R(0) = [-2, 2]$| and

$$\Psi (0)=\frac{1}{4{\pi }^2}{\displaystyle \underset{-2}{\overset{2}{\int }}\sqrt{(8-4x_2){(x_2+2)}^2}}\text{\hspace{0.5em}d}{x}_2=\frac{64}{15{\pi }^2}.$$

In our notation |$\Phi(x)=\Psi(4x)\cdot 4$|⁠, since one can rescale the variable and account for the fact that both functions are assumed to have integral 1. Therefore, |$\Phi(0)=\Psi(0) \cdot 4=\frac{256}{15 \pi^2}$|⁠. □

 

Remark 24.

For |$g=2$|⁠, |$t = \pm 1$|⁠, and |$\operatorname{End}_{\overline{\mathbb Q}}(A) \simeq \mathbb Z$|⁠, we have an equivalent reformulation of (39):

$${\pi }_A(x,t)~\frac{128}{15{\pi }^2}\cdot \frac{m_A|C(m_A,t)|}{|G(m_A)|}\cdot {\displaystyle \prod _{\ell \nmid m_A}\frac{\ell ({\ell }^6-{\ell }^5-{\ell }^4+\ell +1)}{(\ell -1)({\ell }^2-1)({\ell }^4-1)}}\cdot \frac{\sqrt{x}}{\log x}.$$

This is obtained by combining (22) with the value of |$\Phi(0)$| from the previous remark and with the formula

$$|{\mathrm{GSp}}_4(\mathbb{Z}/\ell \mathbb{Z})|={\ell }^4(\ell -1)({\ell }^2-1)({\ell }^4-1).$$

□

 

Remark 25.

For higher |$g$|⁠, the function |$\Phi$| is shown to have a certain general form in Appendix 2. It may again be calculated explicitly using, for example, [49, Theorem 7.8.B] and [30, 5.0.4] (see also the upcoming [7]). □

 

Remark 26.

For |$g=1$|⁠, a more refined version of (1) was proposed in [2]; for higher |$g$|⁠, similar refinements are relegated to future work. □

 

Remark 27.

Variations of our Conjecture 4 may be formulated for non-generic classes of abelian varieties such as the case of a CM elliptic curve |$E/\mathbb Q$| (which was already considered in [35]); in such cases, both the assumption on the image of |$\rho_A$| and the Equidistribution Assumption must be modified appropriately. We relegate such endeavours to future work. □

6 Computations

The Lang-Trotter Conjecture as formulated in (40) has been supported by numerical evidence (see [8, 13, 35]). Among the main ensuing difficulties are the computations of the integer |$m_A$| and of the quotient |$\frac{m_A |C(m_A, t)|}{|G(m_A)|}$|⁠. These may be resolved for |$g=1$| by working with a {Serre curve}, that is, an elliptic curve for which |$\left|\mathbb GL_2\left(\hat{\mathbb Z}\right) : \Im \rho_A\right| = 2$|⁠. For such a curve, the integer |$m_A$| is the least common multiple of |$2$| and the discriminant of |$\mathbb Q\left(\sqrt{\Delta_A}\right)$|⁠, where |$\Delta_A$| is the discriminant of any Weierstrass equation of |$A$|⁠; see [27, Section 4, p. 1558]. As proved in [27] and later in [14], in more than one sense almost all elliptic curves are Serre curves. Examples of such curves, as exhibited by Serre in [41, pp. 310–311] and by Daniels in [16, p. 227], have been used for numerical computations in [16, p. 227].

For higher |$g$|⁠, the investigation of |$m_A$| from a computational perspective is a solid problem in itself that remains to be tackled. In this section, while we do not provide numerical evidence for Conjecture 4, we do provide some computational data that complements our main theoretical results.

Fig. 1.

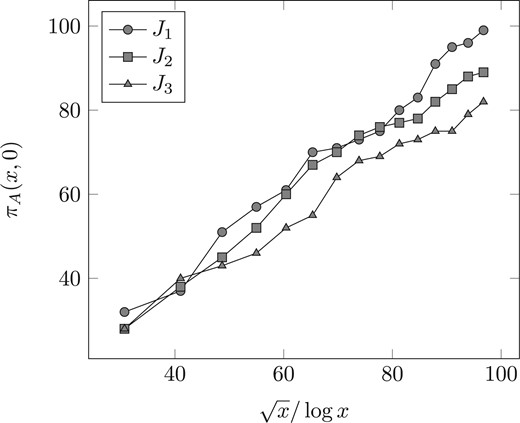
Values of |$\pi_A(x,0)$| versus |$\sqrt{x}/\log x$| for various Jacobians of hyperelliptic curves.

Fig. 2.

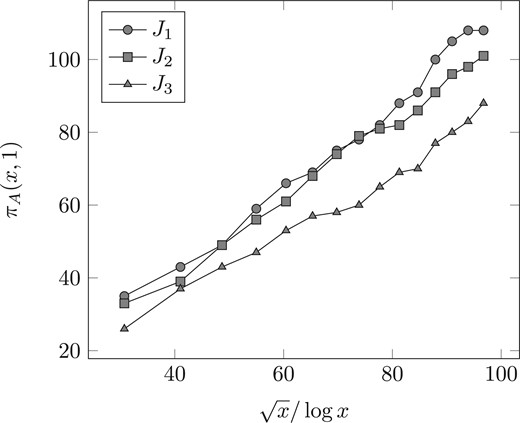
Values of |$\pi_A(x,1)$| versus |$\sqrt{x}/\log x$| for various Jacobians of hyperelliptic curves.

6.1 Values of |$\pi_A(x,t)$|

Figures 1 and 2 show the values of |$\pi_{A}(x, t)$| graphed versus |$\sqrt{x}/\log x$| for |$t \in \{0, 1\}$| and |$A \in \{J_1, J_2, J_3\}$|⁠, where |$J_1, J_2, J_3$| are the Jacobians of the hyperelliptic curves listed in Table 1. Prediction (38) would imply that these graphs approximate a straight line, whose slope is determined by the constant in front of |$\sqrt{x}/\log x$|⁠; the graphs are indeed consistent with this implication.

Table 1.

Jacobians of hyperelliptic curves used in computations

Jacobian	Hyperelliptic curve	Genus	Comments
|$J_1$|	|$y^2 = x^5 - x + 1$|	2	Good reduction outside |$\{ 2, 19, 151 \}$|⁠, |$\operatorname{End}(J_1) \cong \mathbb Z$| [18, p. 509]
|$J_2$|	|$y^2 = 4x^7 - 12x - 35$|	3	Everywhere semistable, |$\operatorname{End}(J_2) \cong \mathbb Z$| [51, p. 2]
|$J_3$|	|$y^2 = 4x^9 - 8x - 39$|	4	Everywhere semistable, |$\operatorname{End}(J_3) \cong \mathbb Z$| [51, p. 2]

Fig. 3.

Average number of |$ \nu(a_{1,p})$| for |$J_1$|⁠, |$J_2$|⁠, and |$J_3$|⁠, in the intervals |$[2^{i-1}, 2^{i}]$|⁠, |$i=2,\ldots, 21$|⁠. For comparison, the graphs of |$\log(\log(2^i))$| and |$\log(\log(2^{i-1}))$| are shown in dotted lines.

6.2 Converging products of Lemma 12

In part (iii) of Lemma 12, we showed that the following infinite product converges for all integers |$t$| and all integers |$g \geq 1$|⁠:

$$P_{g,t}:={\displaystyle \prod _{\ell }\frac{\ell \cdot \left|\right\{M\in {\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z}):\mathrm{tr}M\equiv t(\mathrm{mod}\ell )\left\}\right|}{|{\mathrm{GSp}}_{2g}(\mathbb{Z}/\ell \mathbb{Z})|}}.$$

The numerical value of this product depends on the genus |$g$| and the primes dividing the trace |$t$| (more precisely, the numerator of each factor depends only on whether or not |$\ell \mid t$|⁠). It is possible to compute its value for various |$g$| and |$t$|⁠. For example, when |$g=2$| we can use the explicit formulae of Remark 13. In that case, for |$t \in \{0, 1\}$|⁠, numerical computations show that the products appear to quickly converge to

$$P_{2,0}\approx 1.3547\dots ,P_{2,1}\approx 0.7988\dots .$$

6.3 The normal order of |$\nu(a_{1,p})$|

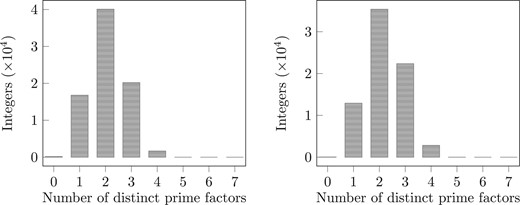
Figure 3 shows the average number of |$\nu(a_{1,p})$| for |$J_1$| of Table 1, for |$p$| in the intervals |$[2^{i-1}, 2^i]$|⁠, |$i = 2, \ldots, 21$|⁠. The graphs of |$\log \log 2^i$| and |$\log \log 2^{i-1}$| are shown for comparison. Figure 4 presents histograms of the values of |$\nu(a_{1,p})$| for |$J_1$| in two intervals: |$[1, 2^{20}]$| and |$[2^{20},2^{21}]$|⁠. The corresponding histograms for |$J_2$| and |$J_3$| are very similar.

Fig. 4.

Histograms of |$\nu(a_{1,p})$| for |$J_1$|⁠; on the left, the data are for primes |$p < 2^{20}$|⁠, and on the right, the data are for primes |$2^{20} < p < 2^{21}$|⁠. Primes of bad reduction and primes for which the trace is zero are excluded.

Funding

This work was partially supported by the National Science Foundation under agreement No. DMS-0747724 (to A.C.C.), by the European Research Council under Starting Grant 258713 (to A.C.C.), by the Simons Collaborative Grant under Award No. 318454 (to A.C.C.), by the National Science Foundation under agreement CNS-0831004 (to A.S.), by the National Science Foundation MSPRF 0802915 (to K.E.S.), by the Natural Sciences and Engineering Research Council of Canada PDF 373333 (to K.E.S.), and by the National Security Agency under Grant H98230-14-1-0106 (to K.E.S.). The United States Government is authorized to reproduce and distribute reprints notwithstanding any copyright notation herein.

Acknowledgments

The authors thank Jeff Achter, Alina Bucur, Hao Chen, Francesc Fité, Nathan Jones, Kiran Kedlaya, Emmanuel Kowalski, Antonella Perucca, Karl Rubin, Jean-Pierre Serre, Drew Sutherland, Cassie Williams, and Jonathan Wise for valuable discussions related to this paper. They are grateful for the hospitality of the Banff International Research Station, Alberta, Canada, and the support of the organizers Chantal David, Matilde Lalín, and Michelle Manes of the conference Women in Numbers 2 (2011), where this work was initiated. The last three authors thank the first author for her leadership and hard work on this project.

Appendix 1. Letter by J-P. Serre on Dimension of Conjugacy Classes in Symplectic Groups

Paris, May 8, 2015

Dear professor Cojocaru,

In case you want optimal estimates for the dimensions of conjugacy classes in |$\operatorname{Sp}$| and |$\operatorname{GSp}$|⁠, here is what one can say:

Let us consider the algebraic groups |$G = \operatorname{GSp}_{2n}$| or |$\operatorname{Sp}_{2n}$| over a field |$k$| of characteristic |$0$| (there are some small changes in char. |$p > 0$|⁠). Assume |$n > 1$|⁠, since the case of |$\mathbb GL_2$| and |$\operatorname{SL}_2$| is obvious. If |$g \in G(k)$|⁠, let |$d(g)$| be the dimension of the conjugacy class of |$g$|⁠, viewed as an algebraic subvariety of |$G$|⁠; we have |$d(g) = \dim G - \dim Z_G(g)$|⁠, where |$Z_G(g)$| is the centralizer of |$g$| in |$G$|⁠.

 

Theorem A.1.

Assume that |$g$| is not of the form |$cu$|⁠, where |$c$| is in the centre of |$G$| and |$u$| is unipotent. Then |$d(g) \geqslant 4n-4$|⁠. If moreover |$\operatorname{Tr}(g) = 0$| and |$n > 2$|⁠, we have |$d(g) \geqslant 4n-2$|⁠. □

A few remarks before giving the proof:

• (1) This is a ‘geometric’ statement: we may assume that the ground field is algebraically closed.

• (2) We may assume that |$G = \operatorname{Sp}_{2n}$|⁠; the case of |$\operatorname{GSp}_{2n}$| follows by writing |$g$| as product of a scalar and an element of |$\operatorname{Sp}_{2n}$|⁠; the dimension of the conjugacy class is the same.

• (3) If |$\operatorname{Tr}(g) = 0$|⁠, then the condition ‘|$g \neq cu$|’ is satisfied, thanks to the fact that the characteristic does not divide |$2n.$|

• (4) The bounds are optimal. One realizes them by using the obvious embedding |$\iota : \operatorname{SL}_2 \to G$|⁠, fixing a non-degenerate subspace of codimension 2. If one chooses |$g = \iota(-1)$|⁠, the centralizer of |$g$| in |$\operatorname{Sp}_{2n}$| is |$\operatorname{Sp}_{2n-2} \times \operatorname{SL}_2$|⁠; its dimension is |$2(n-1)^2 + n-1 + 3 = 2n^2 -3n +4$|⁠; hence the dimension of the conjugacy class of |$g$| is |$\dim G - (2n^2-3n+4) = 2n^2 + n - (2n^2-3n+4) = 4n-4$|⁠. If one chooses |$g = \iota(x)$|⁠, where |$x \in \operatorname{SL}_2$| is such that |$\operatorname{Tr}(x) = 2-2n$| (this is always possible and gives a non-central element because |$2-2n \neq \pm 2$|⁠), one gets an element of trace 0 with centralizer the product of |$\operatorname{Sp}_{2n-2} $| by a group of dimension 1; its dimension is |$2n^2 -3n +2$|⁠, and the dimension of its conjugacy class is |$4n-2$|⁠.

• (5) In the |$\ell$|-adic application, one needs the fact that, if |$g \in \operatorname{GSp}_{2n}(\mathbb Z_\ell)$|⁠, the dimension (as an |$\ell$|-adic manifold) of the conjugacy class of |$g$| is the same as its dimension in the sense of algebraic geometry.

For a given |$t \in \mathbb Z$|⁠, with |$t \neq \pm 2n$|⁠, one needs to choose |$\ell$| so that no element of trace |$t$| of |$\operatorname{GSp}_{2n}(\mathbb Z_\ell)$| can be of the forbidden shape |$cu$| ; as you explain in your paper, this is done by taking |$\ell$| such that |$v_\ell(t/2n) \neq 0$|⁠, which is always possible.

Proof of|$d(g) \geqslant 4n-4$|⁠.

We may assume that |$g$| is semisimple. Indeed, if we decompose |$g$| in Jordan form, as |$g = su = us$|⁠, where |$s$| is semisimple and |$u$| is unipotent, the centralizer of |$g$| is contained in the centralizer of |$s$|⁠, hence |$d(g) \geqslant d(s)$|⁠.

Let us decompose the vector space |$V = k^{2n}$| (with its chosen non-degenerate alternating form) as a direct sum of eigenspaces of |$g$|⁠, say |$V = \oplus V_{\lambda}$|⁠. These spaces have the following properties:

• (a) |$V_1$| and |$V_{-1}$| are non-degenerate, hence of even dimension;

• (b) If |$\lambda \neq 1,-1$|⁠, then |$V_\lambda$| is totally isotropic and in duality with |$V_{\lambda^{-1}}$|⁠.

Put |$n_\lambda = \dim V_\lambda$|⁠. The centralizer of |$g$| is :

$$Z_G(g)={\mathrm{Sp}}_{n_1}\times {\mathrm{Sp}}_{n_{-1}}\times {\Pi }^{\prime }\mathbb{G}L{n}_{\lambda },$$

where the symbol |$ \Pi'$| means a product on a set |$\Lambda$| such that |$k^\times$| is the disjoint union of |$\{1,-1\}, \Lambda$|⁠, and |$\Lambda^{-1}$|⁠.

(It might be more efficient to use the orthogonal decomposition of |$V$| given by the eigenspaces of |$g + g^{-1}$|⁠.)

This implies :

$$\dim Z_G(g)=\frac{1}{2}(n_1^2+n_1+n_{-1}^2+n_{-1})+{\Sigma }^{\prime }{n}_{\lambda }^2,$$

(A.1)

where |$\Sigma'$| means a summation over |$\lambda \in \Lambda$|⁠.

We also have:

$$2n=n_1+n_{-1}+2{\Sigma }^{\prime }{n}_{\lambda }.$$

(A.2)

We now need to give an upper bound for the sum (A.1). Let us simplify the notation by putting |$ x = n_1/2, y=n_{-1}/2, z = \Sigma' n_\lambda$|⁠. Equation (A.2) becomes:

$$n=x+y+z,$$

(A.3)

and equation (A.1) implies (using |$(\Sigma' n_\lambda)^2 \geqslant \Sigma' n_\lambda^2$|⁠):

$$\dim Z_G(g)⩽2x^2+x+2y^2+y+z^2.$$

(A.4)

Consider first the case |$z=0$| (i.e., the case where |$g$| as order 2). In that case, (A.1) shows that |$ \dim Z_G(g) = 2x^2+x+2y^2+y = 2n^2+n - 4xy$|⁠. We have |$xy \neq 0$|⁠, otherwise |$g$| would be central; hence |$x$| and |$y$| run between |$1$| and |$n-1$|⁠. In that range the product |$xy$| is minimum when either |$x$| or |$y$| is equal to 1, in which case its value is |$n-1$|⁠. Hence |$ \dim Z_G(g) \leqslant 2n^2 + n - 4(n-1)$|⁠, i.e., |$d(g) \geqslant 4(n-1)$|⁠, as wanted.

Suppose |$z \geqslant 1$|⁠; we have |$x,y \geqslant 0$|⁠. With the relation (A.2'), this shows that the point |$(x,y,z) \in \mathbb R^3$| belongs to the triangle with vertices the three points |$(0,0,n), (0,n-1,1), (n-1,0,1).$| Since the function |$2x^2+x+2y^2+y+z^2$| is convex, it attains its maximum at one of the vertices [6, Chapter II, Section 7.1, Proposition 1]; its values there are |$n^2, 2n^2-3n+2, 2n^2-3n+2$|⁠. Since |$n^2 \leqslant 2n^2-3n+2$| for |$n \geqslant 2$|⁠, this shows that |$ \dim Z_G(g) \leqslant 2n^2-3n+2$|⁠, hence |$d(g) \geqslant 4n-2$|⁠, and fortiori|$d(g) \geqslant 4n-4$|⁠, as wanted.

(The proof also shows that |$d(g) = 4n-4$| is only possible when |$g$| is an involution of type |$\pm \ \iota(-1)$|⁠, as in Remark 4.)

Proof of|$d(g) \geqslant 4n-2$| when |$\operatorname{Tr}(g)=0$|⁠.

We use the same notation as in the above proof. The case |$z=0$| is possible only if |$n$| is even, with |$x=y = n/2$|⁠. This gives a centralizer of dimension |$n^2+n$|⁠, hence |$d(g) = n^2$|⁠, which is |$> 4n-2$| when |$n \geqslant 4$|⁠. Hence |$z \geqslant 1$|⁠, in which case the computation given above shows that |$d(g) \geqslant 4n-2$|⁠.

Best wishes

J-P. Serre

Appendix 2. Letter by J-P. Serre on the Continuity of the Density Function

Paris, April 12, 2015

Dear Katz,

Thank you very much for your letter about the density problem for |$\operatorname{USp}(2n)$|⁠.

After writing to you I found a different way of getting the same result, based on an integration formula which is a combination of Weyl’s formula and a formula of Steinberg [46, Lemma 8.2].

Let me start with a simple simply connected group |$G$|⁠. Let |$T$| be a maximal torus and define the roots, weights, fundamental weights as usual. I need to number the fundamental weights: |$\omega_1,\ldots, \omega_n$|⁠, where |$n$| is the rank. Call |$\chi_i$| the traces of the corresponding fundamental representations and call |$\psi_i$| their restrictions to |$T$| (I am copying Steinberg’s notations). Steinberg’s formula is a formula relating the |$n$|-differential forms on |$T$| given on one hand by the exterior product of the |$d\psi_i$| and on the other hand by the exterior product of the |$d\omega_i/\omega_i$| (invariant differential on the torus). The formula is as follow:

$$d{\psi }_1\wedge \mathrm{...}\wedge d{\psi }_n=f.d{\omega }_1/{\omega }_1\wedge \cdots \wedge d{\omega }_n/{\omega }_n,$$

(A.5)

where |$f = \omega_0 \prod_{\alpha > 0} (1 - \alpha^{-1})$| and |$\omega_0 = \prod \omega_i$|⁠.

(Note that, here, I am forced to use a multiplicative notation for the roots, since I view them as functions on |$T$|⁠.) We may write |$f^2$| in a slightly simpler form:

$$f^2={\displaystyle \prod _{\alpha >0}(\alpha +{\alpha }^{-1}-2)}.$$

(A.6)

This shows that |$f^2$| is real and invariant by the Weyl group. It can thus be written as a polynomial in the |$\chi_i$| ; let me call |$D$| that polynomial (it is a kind of discriminant: it vanishes only on the singular elements of |$G$|⁠). We thus have:

$$f^2=D({\chi }_1,\dots ,{\chi }_n).$$

(A.7)

This formula of Steinberg gives an integration formula over any local field. Here I shall stick to |$\mathbb R$| but I have no doubt that the |$p$|-adic case should be useful, too. To simplify matters, I shall suppose that -1 is in the Weyl group |$W$|⁠.

Let now call |$UG$| the compact form of |$G$|⁠, and |$UT$| the corresponding torus. The roots |$\alpha$|⁠, and the characters |$\omega_i$| are now viewed as functions on |$UT$| with complex values of absolute value 1. The |$\chi_i$| are real-valued functions (because of my assumption on the Weyl group); let me call them |$x_i$|⁠; they give a map |$x: UG \to \mathbb R^n$| which is well known (since Elie Cartan [9, pp. 803–804]) to have the following properties:

• (a) It gives a homeomorphism of the space |$Cl(UG)$| on to a compact subset |$C$| of |$\mathbb R^n$|⁠.(When |$G$| has type |$G_2$|⁠, the set |$C$| is the one I asked you to draw for me.)

• (b) Let |$C_T$| be the standard fundamental domain of |$W$| (in the tangent space, it corresponds to the fundamental alcove); the map |$C_T \to C$| is a homeomorphism; the boundary of |$C$| corresponds to the singular classes. (I see that by using topological arguments.)

• (c) The function |$D(x_1,\ldots,x_n)$| (where |$D$| is as above) is a polynomial whose restriction to |$C$| is zero on the boundary and nowhere else.

By combining this with H. Weyl’s integration formula, one finds:

 

Theorem A.2.

The image by |$x : UG \to \mathbb R^n$| of the normalized Haar measure of |$G$| has a continuous density (with respect to the standard measure |$dx_1\cdots dx_n$|⁠), namely the function |$\varphi(x_1,\ldots,x_n)$| which is equal to |$0$| outside |$C$| and to |$ (2\pi)^{-n} |D(x_1,\ldots,x_n)|^{1/2}$| on |$C$|⁠. □

 

Corollary A.3.

The equidistribution measure associated with a fundamental character of |$G$| has a continuous density. □

More precisely, the density at a number |$c$| of the fundamental character |$\chi_1$| is equal to |$\int \varphi(c,x_2,\ldots,x_n) dx_2 \cdots dx_n.$|

Curiously, this point of view does not seem to give the fact that such densities are real analytic outside a finite number of values (namely, those taken by the character at the points of finite order of |$G$| corresponding to the vertices of the alcove, i.e. the points of |$G$| of order 1 or 2 when |$G = \operatorname{Sp}_{2n}$|⁠).

One can also say when the density is not 0; for instance, for the trace when |$G= \operatorname{Sp}_{2n}$| the density is nonzero when the trace |$c$| is such that |$-2n < c < 2n$|⁠.

When -1 is not in the Weyl group, some fundamental characters come in pairs of conjugate ones and instead of |$\mathbb R^n$| one should take a product of copies of |$\mathbb R$| and |$ \mathbb C$|⁠. The case of |$\operatorname{SL}_3$| is especially nice; the compact |$C$| lies inside |$\mathbb C$| and is the interior (+ boundary) of a ‘hypocycloid with 3 cusps’ (hypocycloïde á trois rebroussements—as I learned when preparing the ENS competition in 1944-45).

Best wishes

J-P. Serre

PS—The explicit formula for |$\varphi$| in the case of |$\operatorname{Sp}_4$| is given in the aritcle of Fité et al. [21]; see Table 5, last line. Their |$a_1$| is my |$x_1$| and their |$a_2$| is my |$x_2+1$|⁠.