-
PDF
- Split View
-
Views
-
Cite
Cite
M. C. Begelman, J. E. Pringle, Accretion discs with strong toroidal magnetic fields, Monthly Notices of the Royal Astronomical Society, Volume 375, Issue 3, 1 March 2007, Pages 1070–1076, https://doi.org/10.1111/j.1365-2966.2006.11372.x
Close - Share Icon Share
Abstract
Simulations and analytic arguments suggest that the turbulence driven by magnetorotational instability (MRI) in accretion discs can amplify the toroidal (azimuthal) component of the magnetic field to a point at which magnetic pressure exceeds the combined gas + radiation pressure in the disc. Arguing from the recent analysis by Pessah & Psaltis, and other MRI results in the literature, we conjecture that the limiting field strength for a thin disc is such that the Alfvén speed roughly equals the geometric mean of the Keplerian speed and the speed of sound in gas. We examine the properties of such magnetically dominated discs, and show that they resolve a number of outstanding problems in accretion disc theory. The discs would be thicker than standard (Shakura–Sunyaev) discs at the same radius and accretion rate, and would tend to have higher colour temperatures. If they transport angular momentum according to an α prescription, they would be stable against the thermal and viscous instabilities that are found in standard disc models. In discs fuelling active galactic nuclei, magnetic pressure support could also alleviate the restriction on accretion rate imposed by disc self-gravity.
1 INTRODUCTION
The standard theory of geometrically thin accretion discs (Shakura & Sunyaev 1973) has provided a successful framework for understanding the basic physical properties of these objects, and good progress towards understanding the main uncertainty in the theory, the viscosity, has been made since it was realized that the magnetorotational instability (MRI) can drive dynamo action to maintain magnetic stresses (Balbus & Hawley 1998). However, several aspects of disc theory have remained problematic over the years.
Four of these problems stand out. First, observed disc spectra in cataclysmic variables (CVs) deviate significantly from theoretical expectations, even when self-irradiation is taken into account. Moreover, different kinds of CV systems with similar accretion rates often show different spectra. Secondly, the discs in CVs and low-mass X-ray binaries (LMXBs) often appear to be geometrically thicker than expected, suggesting that some additional source of pressure supports the optically thick layers against gravity, over and above the usual mix of gas + radiation pressure. Thirdly, disc models in which the viscous stress is roughly proportional to the total pressure (‘α-models’) – an otherwise plausible assumption – are often predicted to be unstable to perturbations in temperature and surface density. Yet observations of many potentially unstable sources do not show clear evidence of such instabilities. Fourthly, the accretion discs thought to fuel active galactic nuclei (AGN) are predicted to be gravitationally unstable on scales exceeding a fraction of a parsec, yet mass transport does not seem to be disrupted by fragmentation and star formation in many AGN.
In this paper, we propose a mode of disc accretion in which the pressure of the organized toroidal magnetic field dominates over other forms of pressure. On the basis of published numerical simulations, we argue that the MRI-driven dynamo could amplify the toroidal field to a strength that greatly exceeds the gas pressure. Similar arguments were presented by Pariev, Blackman & Boldyrev (2003) and Blaes et al. (2006), but the former focused on the stochastic part of the field, and neither attempted to estimate the field strength from first principles. Arguing on the basis of analyses by Pessah & Psaltis (2005) and others, we suggest that MRI-driven turbulence could amplify the toroidal field to a maximum strength such that the associated Alfvén speed is roughly the geometric mean between the Keplerian speed and the speed of sound in gas. Such a strong field can dominate the disc structure even in regions where radiation pressure dominates over gas pressure. We construct a model of a magnetically dominated α-disc according to this prescription, and show that the additional pressure support both thickens the disc and increases its colour temperature, stabilizes thermal and viscous instabilities, and ameliorates the effects of gravitational instability.
The plan of this paper is as follows. In Section 2, we outline the evidence for anomalous spectra and disc thicknesses in CVs and LMXBs. We defer brief discussions of the stability problems to Section 4. In Section 3, we discuss the numerical evidence supporting strong toroidal fields in discs, and then focus on the Pessah & Psaltis (2005) analysis and results, as well as results in the literature for non-axisymmetric MRI, in order to justify our estimate for the characteristic disc field. In Section 4, we adopt equation (4) as the constitutive relation for the magnetic pressure, and construct a family of simple black hole disc models characterized by an α-viscosity under this assumption. We show that the resulting discs are hotter and thicker than standard discs. Most importantly, and in contrast to the inner regions of standard black hole disc models, they are not subject to thermal or viscous instabilities. In addition, in the outer regions of AGN discs, where self-gravity is important, they can carry much larger mass fluxes without fragmenting due to gravitational instability. Finally, we discuss our results and summarize our conclusions in Section 5.
2 PROBLEMS WITH CATACLYSMIC VARIABLE AND LOW-MASS X-RAY BINARY DISC MODELS
2.1 Spectral properties
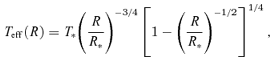
 , by
, by 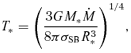
The astronomical objects to which this formula should be most straightforwardly applicable are the accretion discs in CVs, and in particular the discs in nova-like variables, and dwarf novae in outburst. In the nova-like variables, and in the Z Cam variables in standstill, the discs are in steady state in that the time-scale for variation in the accretion rate (measured by system brightness) is much longer than the viscous time-scale (as deduced empirically from the evolution time-scale for dwarf nova outbursts). Indeed, even in dwarf novae in outburst, and especially in superoutburst, the discs are close enough to being in steady state that their spectra should be readily calculable. Estimates of accretion rates and evolution time-scales imply that these discs are optically thick. Thus, if the accretion energy is deposited within the body of the disc (where most of the matter resides), computing the spectra should be closely akin to the well-understood problem of computing the spectra of stellar atmospheres, especially given that in this case the temperatures and gravities (densities) involved are in the standard range (Wade & Hubeny 1998).
However, it has long been known that this simple-minded approach does not give satisfactory results. Just from an empirical point of view it was already clear that there might be problem: in her review of IUE spectra, la Dous (1991) showed that in the range λλ1200–3000 the continuum spectra of dwarf novae at the peak of an outburst are significantly ‘bluer’ (i.e. have more flux at shorter wavelengths) than the continuum spectra of non-magnetic nova-like stars. For the nova-like variables, which should most closely approximate steady-state discs, it turns out that it is difficult, if not impossible, to replicate the ultraviolet (UV) data using steady-state disc models constructed from local thermal equilibrium (LTE) stellar atmospheres (Wade 1988; Long et al. 1994; Orosz & Wade 2003). In general, the models predict UV spectra that are too ‘blue’, and in addition it is not possible to match both the observed flux and the colour at the same time. Similar problems are found for dwarf novae at the peak of outburst (Knigge et al. 1997).
2.2 Disc thickness
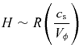
In order to fit the eclipse profiles of discs in CVs, it is necessary to allow for the fact that the disc is not flat, and for the fact that the disc photosphere is usually at a height of a couple of disc scaleheights above the disc mid-plane. Eclipse fitting does allow some estimation of the disc thickness, usually in terms of the value of H/R at the outer disc edge. The observationally inferred values of disc thickness required to fit eclipse observations are typically a couple of times larger than the theoretical estimates (Robinson, Wood & Wade 1999; Shafter & Misselt 2006).
There are other indications of material farther out of the plane than simple estimates would suggest, notably the ‘iron curtain’ material seen both in quiescent discs (Horne et al. 1994) and at high mass-transfer rates (Baptista et al. 1998), and transient non-axisymmetric features, possibly spiral structure seen in tenuous layers of the atmosphere (Steeghs, Harlaftis & Horne 1997), which may require an unusually hot, or thick, component of the atmosphere and/or additional tidal heating at the disc edge (Ogilvie 2002).
LMXBs (White & Mason 1985; Hakala, Muhli & Dubus 1999) and the Algol binary W Cru (Pavlovski, Burki & Mimica 2006) provide more evidence that the outer disc edge does not fit simply with standard disc theory, in that the outer disc edge seems to be thick and structured. In addition, the apparent paucity of eclipses among LMXBs, or bulge sources, indicates that the disc manages to obscure the view of the central X-ray source from a larger fraction of the sky than might be expected (Milgrom 1978; Joss & Rappaport 1979).
The disc rim may not be the ideal place to test standard disc theory, since the outer disc edge is subject to both the tidal dissipation and the impact of the accretion stream (Lubow 1989; Armitage & Livio 1998). Nevertheless, the soft X-ray transients do seem to indicate that in these objects the disc thickness is larger than expected at most radii, and not just at the outer disc edge. This is because, in order to explain the prolonged nature of the outbursts and the shape of the decay light curve, the simplest explanation appears to be that the disc is significantly irradiated from the centre (King 1998). According to standard disc models, such irradiation is not possible, since the inner parts of the disc screen the outer regions (Dubus et al. 1999). However, one can provide an adequate description of the outbursts of soft X-ray transients by assuming that the disc is thicker than simple models predict, allowing significant irradiation to occur (Dubus, Hameury & Lasota 2001).
3 HOW STRONG ARE DISC MAGNETIC FIELDS?
It seems likely that the problems discussed above (and several to be discussed later) could be resolved by considering the dynamical effects of magnetic fields in accretion discs. In standard disc theory, spectral predictions are based on two assumptions: first, that energy is deposited where most of the mass is, and secondly, that the density structure of the disc is smooth and homogeneous. However, it has long been realized that if the process that taps the shear energy, first converts it to magnetic energy, which is then dissipated, then much of the energy can be deposited in a small fraction of the mass (Lynden-Bell 1969; Mészáros, Meyer & Pringle 1977). Moreover, it has also long been known that if a disc is strongly magnetic, it is likely to be highly inhomogeneous (Pustilnik & Shvartsman 1974). In recent models of spectrum formation in the low/hard state of discs in LMXBs and for the hard X-ray flux in AGN, these ideas are taken to the limit in which all the accretion energy is assumed to be deposited in a low-density, extended magnetic corona (see e.g. Done & Nayakshin 2001; Życki, Done & Smith 2001; Barrio, Done & Nayakshin 2003, and references therein).
Numerical simulations give some support to these ideas. Hirose, Krolik & Stone (2006) and Fromang & Nelson (2006), following on from earlier work by Miller & Stone (2000), presented the results of shearing-box simulations of MRI-driven accretion discs, in which the vertical extent of the computational grid is large enough to encompass regions of low gas density. The typical structure that they found is a magnetic sandwich, with most of the mass forming a gas pressure dominated disc in the plane, but with extensive, low-density, magnetically supported layers on either side. In these simulations, most of the energy dissipation still occurs in the gas pressure dominated central layer, and therefore at high optical depth. However, the optical depth of the extended magnetic atmosphere is non-negligible, and this has two effects. First, the density at the effective photosphere is lowered, increasing the ratio of scattering to absorptive opacity, and so giving rise to a slightly harder spectrum (Blaes et al. 2006). Secondly, the height of the apparent photosphere is increased, making the disc appear thicker than a standard disc.
In this paper, we raise the possibility of there being a second equilibrium distribution for the magnetic flux in a disc, namely one in which the magnetic pressure (pB=B2/8π) dominates at all heights in the disc (or at least through most of the pressure scaleheight). The existence of such a distinct class of discs has been raised before by Shibata, Tajima & Matsumoto (1990). As we discuss below, such a possibility would be difficult to simulate numerically because of the small length-scales of the instabilities that maintain the magnetic dynamo. It is also likely that the formation of such a strongly magnetized disc requires special conditions of some kind. For example, Pringle (1989) discussed the formation of a strongly magnetized region in an accretion disc boundary layer, where the strong shear leads to a much higher formation rate for toroidal flux. A disc might also become strongly magnetically dominated as a result of thermal instability, for example, in the central regions of black hole accretion discs (Machida, Nakamura & Matsumoto 2006), or during the transit to quiescence in a CV disc (Tout & Pringle 1992). In these circumstances, the disc is originally hot, with pB∼αpg, where pg is the gas pressure and α is the Shakura & Sunyaev (1973) viscosity parameter. The disc then cools (reducing p but not pB) rapidly on a thermal time-scale (∼1/αΩ, where Ω is the angular speed). This would result in a disc in which β=pg/pB≪ 1.
Pariev et al. (2003) have considered the structure of a strongly magnetic disc in which β≪α∼ 1, but were unable to predict the strength of the field. In this paper, we attempt to quantify the characteristic strength of the toroidal magnetic fields likely to dominate accretion discs, and to explore the consequences of these strong fields for vertical and radial disc structures. We base our estimate of the limiting field strength on a recent analysis of the effects of strong toroidal fields on MRI by Pessah & Psaltis (2005), as well as other analyses in the literature. We assume that toroidal fields are amplified by dynamo action resulting from the turbulence driven by MRI, and are probably limited by buoyancy effects operating on some multiple of the dynamical (orbital) time-scale. As long as MRI grows on a dynamical time-scale, the azimuthal field, Bφ, continues to be amplified, but when the MRI growth rate is suppressed by magnetic tension the growth stops and Bφ saturates.
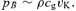
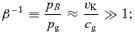
3.1 MRI and the limiting toroidal field strength
In this section, we analyse the physics behind the limiting field strength, and show its relationship to other stability results in the literature. Pessah & Psaltis (2005) considered a differentially rotating, cylindrical equilibrium flow with no z-dependence. In their analysis, they made approximations that correspond to assuming that the flow is of uniform density and contains a uniform poloidal field Bz≠ 0 and a uniform toroidal field Bφ (their results can be generalized to include a radial gradient of Bφ). The angular velocity is taken to be of the form Ω∝R−q. They considered only axisymmetric perturbations, and this enabled them to carry out a local stability analysis and to obtain a local dispersion relation relating wave frequency ω and wavevector k= (kR, 0, kz), in cylindrical polar coordinates (R, φ, z). Their analysis differs from previous work in that they took account of both compressibility and geometrical terms. They focused on the case kz≫kR in order to study how the MRI modes are affected by the strength of the azimuthal field.
In such a configuration, one might expect to encounter two different types of instability: (i) the MRI, which uses the magnetic field (here the poloidal component, which is why we require Bz≠ 0 and kz≫kR) to tap the energy in the shear, and (ii) buoyancy-driven instability, which makes use of the radial structure of the equilibrium configuration to tap the (radial) effective gravity. Pessah & Psaltis found three regions of instability. Regions I and II (see their figs 3 and 5) seem to correspond to the two types of instability mentioned above.
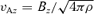 , to cross one (vertical) wavelength (λ∼ 1/kz) is longer than the orbital time 1/Ω. This is the standard criterion for instability to MRI, and corresponds physically to the situation in which a vertical field line is unable to straighten itself fast enough to counter rotational effects (centrifugal force). Thus, instability requires
, to cross one (vertical) wavelength (λ∼ 1/kz) is longer than the orbital time 1/Ω. This is the standard criterion for instability to MRI, and corresponds physically to the situation in which a vertical field line is unable to straighten itself fast enough to counter rotational effects (centrifugal force). Thus, instability requires 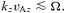
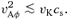
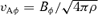 is the azimuthal Alfvén speed, vK is the Keplerian azimuthal velocity and cs is the speed of sound. The regime we are interested in corresponds to a suprathermal, strongly azimuthal field, so that cs≪vAφ≪vK and Bz≪Bφ. This regime differs from the situation in which the predominant field is Bz in two important respects. First, the azimuthal field exerts an additional restoring force for a kz perturbation, which, for a given kz, dominates at large Bφ. Secondly, the length of a field line corresponding to one vertical wavelength (λ∼ 1/kz) is now
is the azimuthal Alfvén speed, vK is the Keplerian azimuthal velocity and cs is the speed of sound. The regime we are interested in corresponds to a suprathermal, strongly azimuthal field, so that cs≪vAφ≪vK and Bz≪Bφ. This regime differs from the situation in which the predominant field is Bz in two important respects. First, the azimuthal field exerts an additional restoring force for a kz perturbation, which, for a given kz, dominates at large Bφ. Secondly, the length of a field line corresponding to one vertical wavelength (λ∼ 1/kz) is now 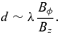
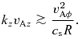
Pessah & Psaltis suggested that Type II instability corresponds to buoyancy modes, in line with the results of Kim & Ostriker (2000) for the limit cs→ 0. Modes of Type I and Type II are clearly linked in some way, as they undergo an exchange of stability at the critical azimuthal field strength. Type II modes are unstable only when both inequalities (6) and (9) are violated, and this only occurs for large values of the azimuthal field strength Bφ > Bcrit. Thus, for a given vertical field strength Bz, MRI modes – which tap the shear energy – are able to operate for small kz and Bφ < Bcrit, whereas for Bφ > Bcrit, radial buoyancy modes, with large kz, take over.
The derivation of the stability criterion by Pessah & Psaltis requires the presence of a vertical field (Bz≠ 0), however small. However, analogous behaviour is found for the case in which the field is purely azimuthal (Terquem & Papaloizou 1996). Since MRI draws its energy from the background shear, it is evident that instability can arise in this case only for non-axisymmetric modes. Terquem & Papaloizou used trial local displacements to show that the linear operator describing the evolution of the linearized equations has a dense or continuous spectrum of oscillation frequencies, ω, that satisfy a local dispersion relation. Their analysis is restricted to modes that are essentially incompressible in the (R, z)-plane.1 This eliminates the fast magnetosonic mode, which in any case is not involved in MRI, and means that the dispersion relation is only a quartic in ω.
In the limit we are considering, with kz≫kR and cs≪vA≪vK, the Terquem & Papaloizou dispersion relation simplifies considerably. For axisymmetric (m= 0) disturbances, ω is real, implying stability. For non-axisymmetric disturbances, we consider first modes with 0 < m≲vK/vA. For these modes, the time-scale for an azimuthal magnetic wave, with wavespeed vA, to cross one (azimuthal) wavelength (∼R/m), is longer than the orbital time 1/Ω (cf. condition 6). For this range of m, there are two low-frequency roots which can be unstable (in addition to two stable roots with ω+mΩ≈±Ω). What is interesting for our current discussion is that the criterion for instability corresponds approximately to condition (7) derived by Pessah & Psaltis. The growth rates are of the order of ∼mcs/R, and the (real parts of the) frequencies in the rotating frame are such that ω+mΩ∼mv2A/R2Ω≲vA/R.
For higher values of m, such that m≳vK/vA, one finds instability, provided that m≲vA/cs. Putting these two conditions together thus implies that for instability we require v2A > csvK, which is the reverse of condition (7). This may correspond to the exchange of stabilities found by Pessah & Psaltis between their modes of Type I and Type II. The growth rates for these high-m modes are ∼vA/R, and the real parts of the frequencies in the rotating frame are small, ω+mΩ∼Ω/m. The fact that these modes are almost stationary in the corotating frame and that the growth rates depend on the field strength suggests, as for the Pessah & Psaltis Type II modes, that they are driven by buoyancy.
The analogy between the findings of Pessah & Psaltis for axisymmetric modes in the limit of 0 < Bz≪Bφ, and the analysis of Terquem & Papaloizou for non-axisymmetric modes when Bz= 0, seems to imply that the same physical processes are at work in both cases.
The basic conjecture of this paper is that amplification of the toroidal magnetic field occurs only while MRI is available to drive a dynamo. Since MRI dies out as Bcrit is approached from below, we assume that Bφ saturates at roughly this level. Indeed, the growth rates of both Type I and Type II modes are small in the vicinity of Bcrit, where the exchange of stability between MRI and buoyancy modes occurs. However, even if Bφ managed to cross this bottleneck and buoyancy modes were excited, this does not mean that Bφ will continue to grow. Since buoyancy modes do not tap the shear, they are unlikely to drive a dynamo capable of amplifying the toroidal magnetic field.
4 CONSEQUENCES FOR DISC STRUCTURE
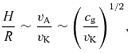
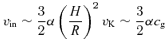
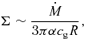
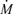 is the local mass-accretion rate through the disc.
is the local mass-accretion rate through the disc.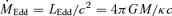 , where κ is the opacity and M is the mass of the central object. Defining
, where κ is the opacity and M is the mass of the central object. Defining 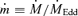 and x≡R/Rg, we obtain an expression for the transverse optical depth through the disc:
and x≡R/Rg, we obtain an expression for the transverse optical depth through the disc: 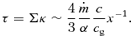
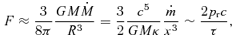
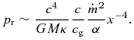
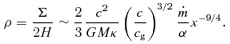
The results presented so far are fully general. To obtain numerical results from them, however, one must determine the value of cg and check whether vA > cr. This depends on the equation of state, the opacity, and the relative importance of radiation and gas pressure, which we now address.
4.1 The inner regions of black hole accretion discs
4.1.1 The disc structure
We consider here the inner regions of a standard Shakura–Sunyaev disc around a black hole where radiation pressure dominates over gas pressure at small radii for values of 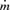 that are not too small. The opacity is dominated by electron scattering and we take κ=κes= 0.4 cm2 g−1. We begin by calculating the magnetically dominated disc structure under the assumption pB > pr. We then check the self-consistency of this assumption a posteriori, to find the radius within which pr >pB and magnetic support can be neglected.
that are not too small. The opacity is dominated by electron scattering and we take κ=κes= 0.4 cm2 g−1. We begin by calculating the magnetically dominated disc structure under the assumption pB > pr. We then check the self-consistency of this assumption a posteriori, to find the radius within which pr >pB and magnetic support can be neglected.
To determine both cg and pr, we assume that the radiation inside the disc is in LTE and set T=TLTE= (3pr/a)1/4. We then use equation (15) to solve for T with cg= (kT/μ)1/2, where μ≈ 0.6 mp is the mean mass per particle. We verify the LTE assumption a posteriori. We find that vA > cr for 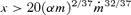 , implying that magnetic pressure dominates over other forms of pressure at all radii, except possibly for the region immediately outside a black hole or neutron star. Radiation pressure dominates over gas pressure for
, implying that magnetic pressure dominates over other forms of pressure at all radii, except possibly for the region immediately outside a black hole or neutron star. Radiation pressure dominates over gas pressure for 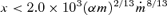 , but since magnetic pressure determines the vertical structure through most of this region, there is no difference in properties between the radiation and gas pressure dominated zones.
, but since magnetic pressure determines the vertical structure through most of this region, there is no difference in properties between the radiation and gas pressure dominated zones.
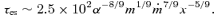
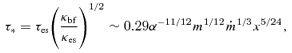
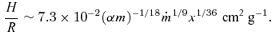
4.1.2 Thermalization and colour temperature
Photospheric colour temperatures typically exceed effective temperatures in the inner regions of standard accretion discs because the radiation is thermalized at a significant scattering optical depth. Colour corrections of luminous accretion discs, fcol≡Tcol/Teff, usually lie in the range ∼1.5–2 (Shimura & Takahara 1995; Davis et al. 2005), corresponding to a scattering optical depth ∼5–20 at the thermalization layer. When τ* > 1, the colour correction is given roughly by fcol∼ (κes/κ*)1/8, where κ* is the absorption opacity evaluated at the local disc colour temperature and at the density of the thermalization layer, ρ*.
An accurate calculation of the colour correction requires a detailed model for the structure of the disc photosphere, which is beyond the scope of our one-zone model for the vertical structure. However, it is clear that a magnetically supported disc should have a higher colour temperature than the equivalent Shakura–Sunyaev model (Blaes et al. 2006). Here, we make a crude estimate of this effect.
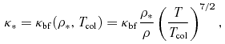
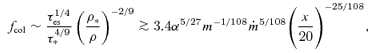
4.1.3 Thermal and viscous stability
A major problem with standard α-disc models is that they are viscously and thermally unstable in their inner regions where electron scattering dominates the opacity (Lightman & Eardley 1974; Pringle 1976; Shakura & Sunyaev 1976). In contrast, the magnetically supported disc models we propose here are not subject to these thermal and viscous instabilities. In all radiative α-disc models in which the opacity is dominated by electron scattering, the dissipative heating rate scales as Q+∝H2Σ and the radiative loss rate scales as Q−∝pr/Σ∝T4/Σ, where we assume LTE. From equation (10), we find T∝H4 at fixed R, implying that Q−∝H16/Σ. At constant Σ, losses increase with H much more rapidly than heating, implying that the magnetically supported discs are thermally stable. This result can be contrasted to a radiation pressure dominated α-disc, in which T∝H1/4, implying instability. (Gas pressure supported α-discs, on the other hand, are thermally stable.)
Now consider viscous instability. On viscous time-scales, thermal balance is maintained, implying Q+=Q−. Therefore, Σ∝H7 for the magnetically supported disc. The viscous couple satisfies G∝H2Σ∝Σ9/7. Since the viscous couple is an increasing function of surface density, the disc is stable (Lightman & Eardley 1974; Pringle 1981).
4.2 The thickness of CV and LMXB discs
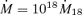 g s−1≈ 10−8 M⊙ yr−1. This corresponds to the outer regions of the disc of a dwarf nova in outburst or of a nova-like variable. Under the standard assumptions, the thickness of such a disc would be H/R∼ 0.05 (see e.g. Frank, King & Raine 2002). However, if we use the assumption of strong toroidal fields put forward in this paper, we find that the disc thickness is given by
g s−1≈ 10−8 M⊙ yr−1. This corresponds to the outer regions of the disc of a dwarf nova in outburst or of a nova-like variable. Under the standard assumptions, the thickness of such a disc would be H/R∼ 0.05 (see e.g. Frank, King & Raine 2002). However, if we use the assumption of strong toroidal fields put forward in this paper, we find that the disc thickness is given by 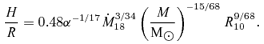
From this we see that the strongly magnetized discs proposed here are not only thicker than standard ones by about an order of magnitude, but also slightly more flared, with H/R∝R0.132 rather than the usual ∝ R0.125. Thus, such discs are more subject to irradiation from a central luminosity source.
4.3 Reduction in disc self-gravity
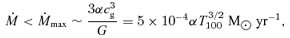
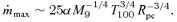
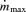 with R continues out to a radius RBH, where the gravitational potential of the galaxy is comparable to that of the black hole. If the galactic nucleus is represented by a singular isothermal sphere with velocity dispersion σ, the ‘bottleneck’ occurs at RBH∼GM/2σ2– beyond RBH, the carrying capacity of the disc, at fixed T, is independent of radius. If we use the M–σ relation (Ferrarese & Merritt 2000; Gebhardt et al. 2000; Tremaine et al. 2002), M9∼ 0.13(σ/200 km s−1)4, to eliminate σ in favour of M, we obtain
with R continues out to a radius RBH, where the gravitational potential of the galaxy is comparable to that of the black hole. If the galactic nucleus is represented by a singular isothermal sphere with velocity dispersion σ, the ‘bottleneck’ occurs at RBH∼GM/2σ2– beyond RBH, the carrying capacity of the disc, at fixed T, is independent of radius. If we use the M–σ relation (Ferrarese & Merritt 2000; Gebhardt et al. 2000; Tremaine et al. 2002), M9∼ 0.13(σ/200 km s−1)4, to eliminate σ in favour of M, we obtain 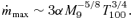
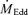 without an efficiency factor, so
without an efficiency factor, so 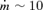 is required to produce an Eddington luminosity with an efficiency of 0.1.)
is required to produce an Eddington luminosity with an efficiency of 0.1.)5 DISCUSSION AND CONCLUSIONS
We are well aware of the speculative nature of some of the assumptions that have gone into our proposed disc model. Our proposal that vA saturates at ∼(csvK)1/2 is an educated guess based on a very simple interpretation of the likely conditions under which MRI is able to drive strong turbulence. We implicitly assume that MRI operates at all heights above the disc mid-plane, amplifying Bφin situ; however, Bφ may also be advected to high latitudes by buoyancy. If buoyant transport from below dominates, then vA could be even larger than we suggest.
The surviving MRI modes when vA≫cs have large kz, implying that the resulting turbulence would be driven on small scales. This is in contrast to the more common assumption in MRI calculations, that vA≪cs, in which case turbulence is driven on scales up to the disc thickness. In order to build up the strong, large-scale toroidal field in our picture, the dynamo might have to involve an inverse cascade, the possibility of which is by no means certain. If the production of a large-scale toroidal field is not efficient in this limit, then our proposed field strength could be a considerable overestimate.
Alternatively, we have suggested the possibility that accretion discs with strong toroidal fields of the kind we discuss here may form a second stable branch of accretion disc configurations, perhaps only accessible through some sudden change in properties – for example, a thermal instability (cf. Section 3). This kind of bimodality of thin discs could help explain the spectral differences of otherwise similar accreting white dwarf systems in CVs (cf. Section 2.1).
Whether or not our quantitative estimate of the saturated field strength is accurate and physically realized, we wish to emphasize the role that a magnetic ‘equation of state’– a relation between a suprathermal Bφ and other fluid variables – could play in altering the structure and stability properties of α-discs.
Note that this restriction still permits the effects of compressibility to operate in the azimuthal direction.
We thank Keith Horne, Frank Verbunt, Richard Wade and Gordon Ogilvie for helpful discussions. MCB acknowledges support from NSF grant AST-0307502 and from the University of Colorado Council on Research and Creative Work. He thanks the Institute of Astronomy and Trinity College, Cambridge for hospitality. JEP thanks the Fellows of JILA for their hospitality.
REFERENCES



