The evolution of triples with a Roche lobe filling outer star

Abstract

The evolution of triples has not attracted much attention in the literature, although their evolution can be dramatically different from binaries and single stars. Triples are quite common, and we find that for about 1 per cent of the triples in the Tokovinin catalogue of multiple stellar systems in the solar neighbourhood, the tertiary star will overflow its Roche lobe at some time in its evolution, before any of the inner stars leave the main sequence. For two of these systems, ξ Tau and HD 97131, we simulate in detail this phase of mass transfer, during which stellar evolution, gravitational dynamics and hydrodynamics all play an important role. We have used amuse to solve these physical processes in a self-consistent way. The resulting evolution, mass transfer and the effects on the inner as well as on the outer orbit are profound, although it is not trivial to predict the eventual consequence of the phase of mass transfer and the appearance of the resulting system.

gravitation, hydrodynamics, methods: numerical, binaries: close, stars: evolution

INTRODUCTION

Stars tend to be formed in pairs, and many of these binaries are found to be the member of a triple or even higher order system. Multiple star systems are generally hierarchical, i.e. a binary is orbited by another star or another binary, etc. (Hut & Bahcall 1983). Democratic triples (or higher order systems) tend to be short-lived and dissolve to lower order systems (van den Berk, Portegies Zwart & McMillan 2007).

The evolution of triples has not attracted much attention in the literature, in part due to the complications which already arise in the study of binary systems, and which only become more severe for higher order systems. Most studies of triples discuss the complicated dynamical evolution without paying much attention to the stellar aspect, whereas others focus on the stellar evolution aspects but ignore the non-regular dynamics (Eggleton & Kiseleva 1996; Iben & Tutukov 1999; Kuranov, Postnov & Prokhorov 2001). The majority of these studies focus on the formation of X-ray binaries (Eggleton & Verbunt 1986), millisecond pulsars (Portegies Zwart et al. 2011) and/or Type Ia supernovae (Hamers et al. 2013).

Some studies focus on how the evolution of the triple is affected by the non-linear gravitational dynamics of the three stars, for example, by the effect of Kozai resonances (Kozai 1962), but the hydrodynamical effects are often reduced to semi-analytic approximations (see Eggleton & Verbunt 1986). In all cases the presence of a third star has a major effect on the evolution of the entire system, and the resulting product is considered rather exotic. Triple evolution, for that reason, is often adopted to explain exotic systems.

Triples, however, are quite common (Tokovinin 2010) and a large fraction of stars, and therefore of binaries, are affected by the evolution of the third companion. In most cases these mutual influences are minor in the sense that the third, outer star affects the evolution on the inner binary at a level that is not reaching a part of parameter space inaccessible by normal binary evolution. In those cases the presence of a third star has no extraordinary effect on the evolution of an inner binary, and regular binary evolution plus a single star that happens to be relatively nearby can be adopted to describe the system. In some, relatively rare, cases there is strong mutual interaction, and topology and orbital parameters of the system require a special treatment to understand its future evolution. These cases are possibly less rare than we might think naively, and in this paper we will discuss a seemingly rare case of triple evolution in which gravity, stellar evolution and hydrodynamics play an important role.

The Tokovinin catalogue of multiple stellar systems in the solar neighbourhood contains 725 triples (Tokovinin 2010). In 130 (∼18 per cent) of these, the outermost star happens to be the most massive star in the system, and is therefore expected to leave the main sequence and evolve along the giant branch before any other star in the system. If the outer orbit is sufficiently small, the tertiary star may overflow its Roche lobe at some time in its evolution. The consequences of this rather exotic scenario are profound, and in this paper we study the effects of Roche lobe overflow (RLOF) of a tertiary star to an inner binary.

Upon a search for how often this scenario could possibly occur, we found a total of six systems in the Tokovinin (2010) catalogue that comply with our criteria. In these six systems we found that the semimajor axis of the outer orbit is sufficiently small for the tertiary star to overflow its Roche lobe at some time in its evolution, before any of the inner stars leave the main sequence. In those cases, mass will be transported from the outer star on to the inner binary.

We simulate in detail the consequence of the onset of mass transfer for two of these systems, ξ Tau and HD 97131, using a combination of stellar evolution, gravitational dynamics and hydrodynamics. The resulting evolution, mass transfer and the effects on the inner as well as on the outer orbit are profound, although it is not trivial to predict the eventual consequence of the phase of mass transfer and the appearance of the resulting system.

TRIPLES FOR WHICH THE TERTIARY STAR INITIATES RLOF FIRST

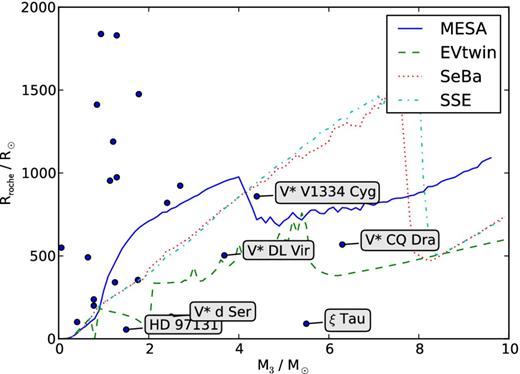
Adopting the Tokovinin (2010) catalogue of 725 multiple stellar systems in the vicinity of the Sun, we selected those triples for which the outer star exceeds the mass of any of the inner stars, leaving a total of 130 triples. In Fig. 1, we show, for the outer component of these triples, the mass and estimated Roche lobe radius (Eggleton 1983), using the orbital parameters provided in the catalogue (see also Table 1).

Figure 1.

Radius of the Roche lobe of the third component of known triple systems versus the mass of the third component (bullets). The curves give the maximum radius reached for a star of a certain mass according to the stellar evolution models mesa (Paxton et al. 2011), evtwin (Eggleton 1971, 2006; Glebbeek, Pols & Hurley 2008), seba (Portegies Zwart & Verbunt 1996) and sse (Hurley, Pols & Tout 2000) for solar metallicity. The triples below the curve are identified and their parameters are listed in Table 1.

Table 1.

Known triples for which the outer (tertiary) star is more massive than any of the two inner stars and the Roche radius is smaller than the maximum size of the star at the tip of the AGB. Columns 1 and 2 give the name and common name of the triple system; column 3 gives the record number within the Tokovinin (2010) catalogue; the numbered notes in column 4 are explained below; columns 5–7 give the masses of the triple components; columns 8–11 give the semimajor axis and eccentricity of the inner and outer orbits; column 12 gives the estimated size of the Roche lobe; columns 13 and 14 give the derived age and mass of the outer component at the onset of RLOF. Remarks: (1) masses from spectral type and therefore very uncertain; (2) orbits may be coplanar (i₁ = 26°, i₂ = 26°; Torres et al. 2003); (3) possibly not even a triple (Wheatley, Mukai & de Martino 2003); (4) tertiary mass uncertain; (5) Lee et al. (2013).

Name	Other name	Cat.	Note	M1	M2	M3	ain	aout	ein	eout	RRoche	tRLOF	MRLOF
		no.		(M⊙)			(au)				(au)	(Myr)	(M⊙)
HD 57061	τ CMa	236	1	17.8	17.8	50.0	0.076	2.49	0.00	0.285	0.95	4.3	41.49
HD 108907	V* CQ Dra	366	3	0.8	0.26	6.3	0.006	5.42	0.00	0.30	2.64	70.1	6.02
HD 21364	ξ Tau	94	1	3.2	3.1	5.5	0.133	1.23	0.00	0.15	0.42	83.7	5.50
HD 203156	V* V1334 Cyg	639		1.62	1.83	4.4	4.616	10.71	0.20	–	3.99	167.6	1.67
HD 120901	V* DL Vir	400	4	2.5	1.4	3.68	0.037	6.68	0.00	0.46	2.34	269.4	3.44
HD 169985	V* d Ser	547	1	2.02	1.94	2.5	0.047	1.94	0.00	0.47	0.62	799.3	2.46
HD 97131	HD 97131	328	2	1.29	0.9	1.5	0.037	0.80	0.00	0.191	0.26	2959.9	1.48
KIC002856960	–	–	5	0.24	0.22	0.76	0.008	0.73	0.0064	0.612	0.12	>H0	0.72

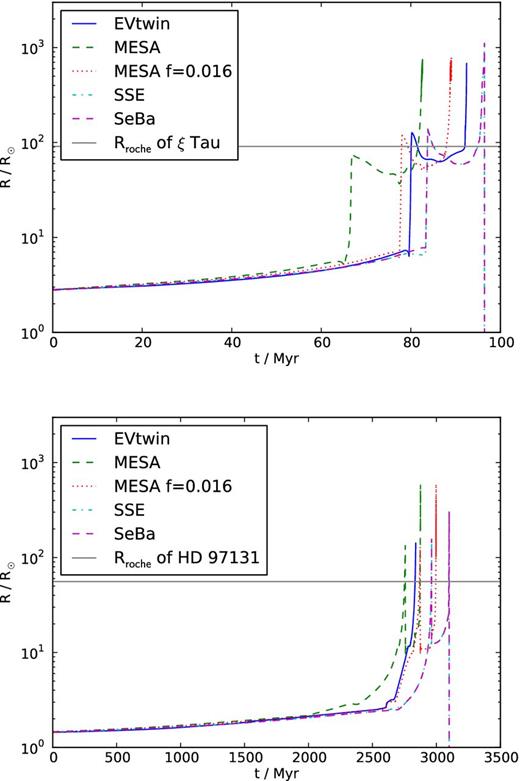
The curves in Fig. 1 give the maximum radius as a function of initial mass, for a series of stellar evolution calculations using a variety of codes. The two parametrized stellar evolution codes, seba and sse, give comparable radii, but because they are mainly based on the same evolutionary track this is not a surprise. The smallest radii come from evtwin, which is a one-dimensional Henyey stellar evolution code with an extensive nuclear network. The code was run until it failed to converge, which generally occurred at the helium flash (1 M_⊙ ≲ M_initial ≲ 2 M_⊙), thermal pulses on the asymptotic giant branch (2 M_⊙ ≲ M_initial ≲ 5 M_⊙) or the carbon flash (M_initial ≳ 5 M_⊙). mesa turns out to be somewhat more stable, in particular for the relatively low-mass ≲4 M_⊙ stars. The differences between mesa and evtwin are quite large, which we mainly attribute to the convergence problems of the latter.

The triples above the curves in Fig. 1 are not expected to engage in a phase of mass transfer initiated by the outer star. For these the tertiary is expected to evolve into a white dwarf. The final phase of these triples, however, can be quite interesting as the extended envelope will pass the inner binary system, much in the same way as was recently studied for planets in orbit around post-common-envelope binary systems (Portegies Zwart 2013). These systems regretfully are beyond the scope of our current study.

Six triples seem to have an orbital separation sufficiently small that the outer star, at some time after leaving the main sequence, will overfill its Roche lobe and transfer mass to the inner binary system. In Fig. 1, we identify those systems by their common name.

For further study we select two of these six systems, with relatively well-constrained orbital parameters. These are ξ Tau and HD 97131, which are likely to develop RLOF near the end and roughly half-way of the first ascend, respectively, both leading to type B mass transfer (Kippenhahn & Weigert 1967).

Interestingly, the third component in these systems tends to be less massive than the inner binary. In this respect, RLOF triples differ fundamentally from binaries, in which the star that first fills its Roche lobe is also the most massive dynamical component. RLOF in triples is therefore expected to be more stable as compared to binaries.

SIMULATIONS

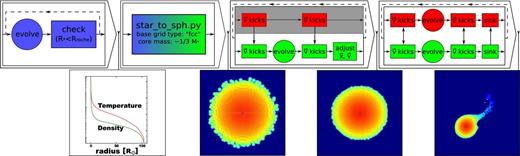
In the evolution of outer RLOF triples, physical processes that play an important role are stellar evolution, gravitational dynamics and hydrodynamics. We have used the Astrophysical Multi-purpose Software Environment (amuse;¹ Portegies Zwart et al. 2009, 2013) to solve all these physical processes in a self-consistent way. A stellar evolution code is used to model the evolution of the outer star prior to RLOF (Section 3.1). At the moment the outer star roughly fills its Roche lobe we stop the stellar evolution simulation and convert the one-dimensional stellar structure from the Henyey code to a three-dimensional hydrodynamical model (Section 3.2). This hydrodynamical model of the outer star is relaxed (Section 3.3) and put in orbit around the binary star (Section 3.4). The complex hydrodynamics of the mass transfer from the Roche lobe filling outer star to the inner binary is followed for several orbits of the outer star while keeping track of the gravitational dynamics of the three stars and the hydrodynamics of the gas from the outer star (Section 3.5). A schematic overview of all these steps is presented in Fig. 2. We advocate the initiative of Shamir et al. (2013) to require source code sharing for publication and make all amuse scripts that were used for these simulations available via the amuse website.

Figure 2.

Schematic overview of the steps taken to simulate triples with a Roche lobe filling outer star. Each of the four arrows describe the amuse solver designed for that step. Inside each combined solver, circles denote the parts performed in optimized component solvers, whereas rectangles denote operations implemented in python/amuse. Colours represent the various domains of physics: red, green and blue correspond to gravitational dynamics, hydrodynamics and stellar evolution, respectively. After each arrow a simple plot is included to illustrate the result of the last step. Note that for the hydrodynamics plots we reduced the SPH smoothing lengths with a factor of 4 for enhanced contrast.

Stellar evolution

Within the amuse framework we currently have the choice of four stellar evolution codes. Two of those utilize parametrized fitting formulae to pre-calculated stellar evolution tracks of full Henyey stellar evolution codes. These codes can be used to acquire a quick assessment of the estimated moment of RLOF of the outer star (like we did in Fig. 1), but are not suitable for the conversion to the hydrodynamical model of the star at the moment of RLOF because information of the internal stellar structure is essential for converting the stellar model to a hydrodynamical realization.

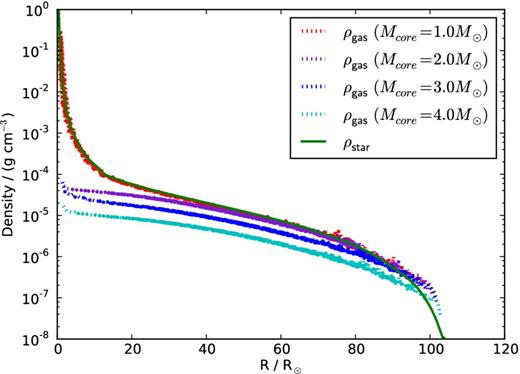
The two Henyey stellar evolution codes in amuse are mesa (Paxton et al. 2011) and evtwin (Eggleton 2006, 1971; Glebbeek et al. 2008). The stellar structure models used in our study are generated using evtwin, but there is no particular reason for this choice over mesa. All stellar evolution calculations in this paper are run with the standard amuse settings for these codes, adopting solar metallicity. By the time the outer star exceeds the radius of its Roche lobe, it already lost some mass and its radius is considerably larger than at birth. The calculated Roche radius R_Roche, along with the age and mass at RLOF, t_RLOF and M_RLOF, is also presented in Table 1. In Fig. 3, the radial density profile of the outer component of ξ Tau is shown at the moment of RLOF (green drawn line)

Figure 3.

Radial density profile of the outer component of ξ Tau at the onset of RLOF (green drawn line). The dotted lines represent SPH models with varying core mass M_core (red, purple, blue and cyan dotted lines for M_core = 1, 2, 3 and 4 M_⊙, respectively). These core masses correspond to a fraction of 0.18, 0.36, 0.55 and 0.73 of the total mass of 5.5 M_⊙.

Converting the Henyey 1D stellar evolution model to a gas particle distribution

Once the radius of the outer star exceeds its Roche limit, the one-dimensional Henyey stellar evolution model is converted to a set of smoothed particle hydrodynamics (SPH) particles. This is realized by inquiring the radial stellar structure profiles for density, temperature, mean molecular weight and radius from the stellar evolution code. Henyey codes divide a star into a set of spherical shells, represented by arrays in which these parameters are stored. Subsequently, we generate a kinematically cold set of N particles with mass M_RLOF/N in a uniform spherical distribution. We now scale the particle positions radially to match the density profile of the star, up to its outer radius R_RLOF. Each particle is subsequently assigned a specific internal energy derived from the temperature and mean molecular mass profiles, which came from the stellar evolution model. This procedure is coded in the standard amuse routine called star_to_sph.py.

This method works very well for stellar evolution models in all phases of the evolution. Because of the use of equal-mass particles and the high concentration of (sub)giant stars, most of the particles, and therefore the highest resolution, will be in the stellar core, whereas the outer edge of the star will remain barely resolved. Most computer time will be spend in the stellar core due to the high density and temperature, but in our triple evolution code, we desire to study the hydrodynamical effects that dominate the outer layers of the star. These outer layers are now ill resolved, and most computer time is spend on parts of the star that are unlikely to affect the dynamics of the outer layers on the short hydrodynamical time-scales associated with RLOF. Relaxing the assumption of equal-mass particles is tricky because of spurious dynamical effects associated with high–low-mass particle interactions. To prevent this, and because we are not particularly concerned about the barely affected (Deupree & Karakas 2005) interior of the Roche lobe filling star, we replace its core with a single mass point. To prevent the star to collapse on to itself, we soften the core particle using Plummer softening (ϵ) and treat it as a pure gravitational point mass without pressure or internal energy. The standard cubic spline of Monaghan & Lattanzio (1985) is used, which declines smoothly to zero at 2.8ϵ. The mass of the core particle is not related to the mass of the hydrogen-exhausted stellar core, but a solution to the numerical difficulties of modelling giant stars without affecting the behaviour of the stellar envelope. It turns out that a core mass of about M_core ≈ M_RLOF/3 gives satisfactory results, as illustrated for ξ Tau in Fig. 3 (red, purple, blue and cyan dotted lines for M_core = 1, 2, 3 and 4 M_⊙, respectively). The core masses used in this figure correspond to a fraction of 0.18, 0.36, 0.55 and 0.73 of the total mass of M_RLOF = 5.5 M_⊙. For lower core masses, M_core < 0.2M_RLOF, the problematic high density at the core remains, while for higher core masses, M_core > 0.5M_RLOF, the density in the envelope starts to deviate appreciably from the stellar structure model. We used a core mass of 2 M_⊙ for ξ Tau and 0.5 M_⊙ for HD 97131.

While replacing the stellar core by a single particle, we correct the density and internal energy profile and solve for the softening length of the core particle. The density and internal energy within the softened region are adapted in such a way that pressure equilibrium is maintained while conserving the original entropy profile. The resulting softening length depends on the mass of the core particle M_core, but typically we found ϵ ≈ 0.2R_RLOF.

Since each of our hydrodynamics simulations covers more than a thousand dynamical time-scales, we adopted a moderate mass resolution with 5 × 10⁴ gas particles. We have performed shorter (five orbits) convergence tests with up to a million particles. We noticed small variations in the orbital parameters, similar in magnitude as the temporal variations in Figs 7 and 8, but the general behaviour was very similar.

Bringing the giant in dynamic equilibrium

Even though the initial particle distribution is as smooth as possible, the initial particle accelerations as computed by the SPH code are not exactly zero. This is probably due a combination of (1) the stellar evolution code and the hydrodynamics code adopting a different equation of state (EOS), specifically using, respectively, a variable and a fixed adiabatic index γ, (2) numerical artefacts of using a (scaled) regular grid in low-density regions, (3) the details of the implementation of gravitational softening of the SPH code and (4) the treatment of particles at the surface, with anisotropic distributions of neighbours. If these non-zero particle accelerations are neglected, this will result in spurious turbulent velocities. Subsequently, viscous dampening will increase the internal energy of the particles. Therefore, some relaxation is still required for our models to prevent artificial heating. Since even at apocentre the giant is distorted from spherical symmetry, we perform the relaxation of the SPH model of the giant star in the potential of the inner binary. Performing relaxation on the giant in the gravitational presence of the inner binary is fairly straightforward in amuse. The combined solver is similar to the one that will be used for resolving the evolution of the triple, except for two minor changes. The gravitational interaction (see Section 3.5) between the giant system (the SPH code) and the inner binary system (the N-body code) is evaluated one-way only: the giant system evolves and feels the forces of the binary, but the binary system remains static. Furthermore, the positions |$\boldsymbol {x}_i$| and velocities |$\boldsymbol {v}_i$| of the particles in the SPH code are adjusted after each step, preserving the centre-of-mass position |$\boldsymbol {R}_\mathrm{com}$| and centre-of-mass velocity |$\boldsymbol {V}_\mathrm{com}$|⁠, and damping the internal velocities by multiplying with a factor f that increases adiabatically from 0 to 1:

\begin{eqnarray} &&{\boldsymbol {x}_{i\mathrm{,\,adjusted}} = \boldsymbol {x}_i - \boldsymbol {R}_\mathrm{com} + \boldsymbol {R}_\mathrm{com, initial}}\nonumber\\ &&{\boldsymbol {v}_{i\mathrm{,\,adjusted}} = f \times (\boldsymbol {v}_i - \boldsymbol {V}_\mathrm{com}) + \boldsymbol {V}_\mathrm{com, initial}.} \end{eqnarray}

(1)

Setting up the triple system

We set up the triple from the orbital parameters taken from the literature, which are listed in Table 1, and convert those to a realization in Cartesian coordinates. The parameters that determine the orientation of the outer orbit relative to the inner orbit are the orbital inclination i, the longitude of the ascending node Ω and the argument of periastron ω. Although the inclination of the inner and outer orbits of ξ Tau and HD 97131 (relative to the plane of the sky) have been measured, their relative orbital inclination is unknown, because the longitude of the ascending node of the outer orbit relative to the inner orbit is unknown for spectroscopic triples.

Of the three parameters defining the orientation, the orbital inclination is expected to have the strongest effects on the mass transfer. We study these effects in Section 4.1 for a wide range in relative orbital inclination. For the orientation of the line of nodes, we adopt the line initially connecting the two inner binary components, for the practical reason that in this case the triple configuration with the giant in hydrodynamical equilibrium is independent of the inclination, allowing us to study the effects of inclination with exactly the same initial conditions. For similar reasons we choose the argument of periastron to be ω = 90°, since for ω close to zero the effects of the inclination probably become negligible.

For both systems the similarity of the inclination of the inner to that of the outer orbit is suggestive of coplanarity. Therefore, we focus mainly on low-inclination systems in the rest of this paper. Note that, as the inclination approaches zero, the choice of longitude of the ascending node and the argument of periastron becomes essentially irrelevant, considering that the inner binary orbit is circular.

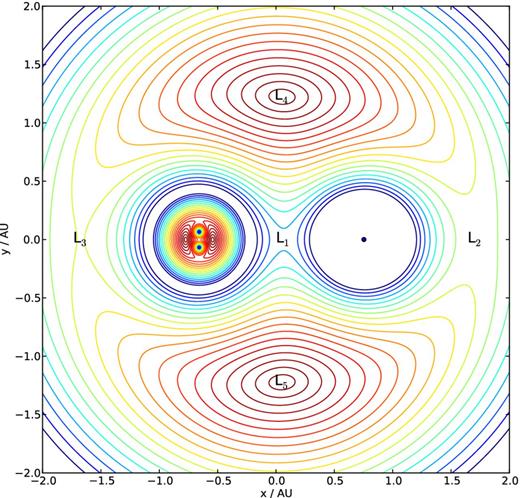
After having constrained all initial conditions, the Cartesian coordinates of the three stars and their masses, we can substitute the outer star (which up to now was considered as a point mass) with the hydrodynamical model from Section 3.3. The resulting triple is then composed of three point masses (the inner two stars and the central core particle of the outer giant star), and the gas particles representing the stellar envelope. A contour plot of the effective potential of ξ Tau in its initial configuration is shown in Fig. 4. The five Lagrangian points are indicated for the outer orbit. The additional set of contours, drawn inside the Roche lobe of the inner binary, also takes into account the centrifugal force due to the rotation of the inner binary.

Figure 4.

Contour plot of the effective potential of ξ Tau in its initial configuration. The five Lagrangian points are indicated for the outer orbit. The additional set of contours, drawn inside the Roche lobe of the inner binary, also takes into account the centrifugal force due to the rotation of the inner binary.

Coupling hydrodynamics with gravity in the evolution model

We perform the simulations of RLOF in triples using a coupled integrator to follow the complex hydrodynamics of the mass transfer from the Roche lobe filling outer star to the inner binary while keeping track of the gravitational dynamics of the stars. The equations of motion of the inner binary are solved using the semisymplectic direct N-body integrator Huayno (Pelupessy, Jänes & Portegies Zwart 2012). The hydrodynamics is performed with the SPH code fi (Pelupessy 2005), using an adiabatic EOS. This choice of EOS was inspired by the fact that the Kelvin–Helmholtz time-scale of the giant is longer than the duration of our simulations by two orders of magnitude. Therefore, we can neglect radiative heating and cooling of the giant's gas. Cooling may become important for the gas that overflows on to the inner binary if a circumbinary disc forms. That is, however, not expected, as discussed in Section 5. If the Kelvin–Helmholtz time-scale were very short, an isothermal EOS would be more applicable. For comparison we performed a test with an isothermal EOS. The giant model in this test was unstable, as expected. The envelope of the giant expands freely, since it is not affected by adiabatic cooling.

For the artificial viscosity the standard form of Monaghan (1992) is used, with α = 0.5, β = 1.0 and η² = 0.01. Although the two inner binary stars are treated as point masses, we allow them to accrete gas from the hydrodynamics particles. This is realized using sink particles which co-move with the mass points in the gravity code. When mass is accreted on to any of these two stars, the masses and momenta of the particles that represent the stars in the N-body integrator are also adjusted properly, and the effects of the increased gravity of the accreting stars are properly taken into account while integrating their equations of motion. For the radius of the sink particles, we adopt a value roughly twice the stellar radius, corresponding to 5 and 2 R_⊙ for the inner binary components of ξ Tau and HD 97131, respectively.

The N-body code as well as the hydrodynamics solver operates on their own internal time steps. The coupling between the two codes is realized using the Bridge method in the amuse framework (see section 4.3.1 in Portegies Zwart et al. 2013). This coupled integrator is based on the splitting of the Hamiltonian much in the same way as is done with two different gravity solvers by Fujii et al. (2007). The difference in our case is that one of the two codes is an SPH code. With the adopted scheme, the hydrodynamical solver is affected by the gravitational potential of its own particles as well as the gravitational potential of the inner binary. The hydrodynamics, in particular the gas drag, in turn affects the orbits of the two inner stars. With Bridge we realize a second-order coupling between the gravitational dynamics and the hydrodynamics. The interval at which the gravity and hydrodynamics interact via Bridge depends on the parameters of the system we study, but typically we achieve converged solutions when this time step is about a fraction of 1/64 of the inner binary orbital period.

RESULTS

Instead of simulating each of the triples in Table 1, we have selected two systems to study in more detail. We chose ξ Tau and HD 97131, without any particular reason other than that they bracket the age range for which the outer star is likely to fill its Roche lobe within a Hubble time and because their masses and orbital parameters are relatively well constrained.

It is infeasible to perform simulations of the hydrodynamics of stars on a stellar evolution time-scale of millions of years. We start our coupled gravity-hydrodynamics simulations when the radius of the outer star significantly exceeds its Roche radius (with overfilling factors R₀/R_Roche = 1.11 and 1.07 for ξ Tau and HD 97131, respectively), to increase the mass-transfer rate in order to better resolve the process of RLOF in triples. This allows us to reliably study the effects of RLOF on the orbital parameters of triples. Mass-transfer rates vary exponentially with the overfilling factor, so we will overestimate it and all consecutive rates of change of orbital parameters. Therefore, the analysis of rates of change is limited to the qualitative behaviour, but we can reliably study the relations between these rates of change.

The case of ξ Tau

The triple ξ Tau is a double-line spectroscopic binary of a 3.2 M_⊙ and a 3.1 M_⊙ star. The circular orbit has a period of ∼7 days. The binary is orbited by a 5.5 M_⊙ giant star in an ∼144 d orbit with an eccentricity of 0.15 (Fekel 1981). The outer star will start to overfill its Roche lobe at an age of ∼80 Myr at a radius of 0.42 au. The mass of the star has by that time reduced to 5.499 M_⊙, but we did not correct the initial orbital separation for this small amount (<0.1  per cent) of mass lost in the stellar wind.

In the top panel of Fig. 5, we present the evolution of the radius of the outer star of ξ Tau as a function of time. The various curves represent the results calculated with different stellar evolution codes. The predicted evolution by sse and seba virtually overlap and predict the longest lifetimes (cyan dash–dotted and magenta dashed line for sse and seba, respectively). evtwin (blue drawn line) gives similar results, but mesa (green dashed line) predicts significantly shorter lifetimes and a smaller radius at the tip of the first giant branch. Most codes indicate that the mode of mass transfer for ξ Tau would be consistent with case B (Kippenhahn & Weigert 1967; Paczyński 1967). With default parameters mesa predicts that it would be case C, but if we include some convective overshooting (as is the default setting for evtwin), mesa agrees on case B mass transfer as well. In Fig. 5, we also included a simulation of the evolution using mesa with a typical value of f = 0.016 (Herwig 2000) for the convective overshoot parameter (red dotted line).

Figure 5.

Evolution of the tertiary star in ξ Tau (top panel) and HD 97131 (bottom panel) as predicted by various stellar evolution codes: evtwin (blue drawn line), mesa with and without convective overshoot (red dotted and green dashed lines, respectively), and seba and sse (magenta dashed and cyan dash–dotted lines, respectively). The horizontal dotted curve gives the size of the Roche lobe of the outer star in ξ Tau and HD 97131 of 0.42 and 0.26 au, respectively.

The inclination i of the orbit is constrained by the observed individual orbital inclinations of the inner and outer orbits, indicating that i ≳ 9° (Fekel 1981). However, a too high inclination would induce Kozai (1962) cycles. Although we do not know the current age of the triple, it appears unlikely to be less than one Kozai cycle. If the relative inclination of the system exceeds i ≳ 45°, episodes of very high eccentricity in the inner binary would have had occurred, which would have initiated tidal effects, mass transfer or even a merger. We cannot formally rule out that some mass transfer may have occurred in the past of the inner binary, but we consider it highly unlikely that i ≲ 45°. We performed several simulations with inclination ranging from i = 9° to 69°.

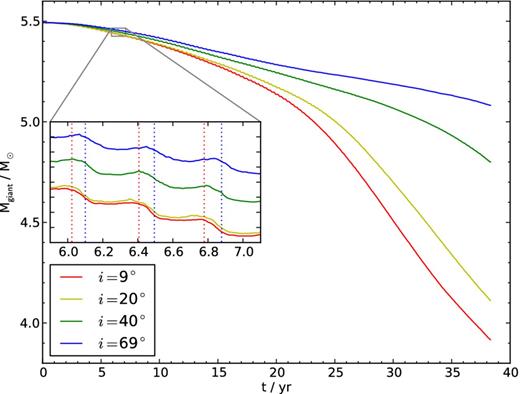
With the adopted parameters the outer star will fill its Roche lobe, while the other (inner binary stars) still reside on the main sequence and are well detached from their respective Roche lobes. In Fig. 6, we present the evolution of the mass of the outer star in four calculations for i = 9°, i = 20°, i = 40° and i = 69°. There is a clear trend, in which high inclination gives a considerably lower rate of mass-loss, and for a lower inclination the rate of mass lost is relatively high. This is expected, because each of the inner binary stars can approach the giant more closely for low inclination where the orbits lie roughly in the same plane.

Figure 6.

Mass of the donor in ξ Tau as a function of time, starting at the onset of RLOF, for a range in initial relative inclination: i = 9° (red), i = 20° (yellow), i = 40° (green) and i = 69° (blue).

The mass-loss from the outer giant is periodic, modulated with the periodicity of the outer orbit. This is a result of the slight eccentricity of the outer orbit, which causes the giant to overfill its Roche lobe at pericentre, whereas after semilatus rectum the star detaches from its Roche lobe, to re-establish RLOF when it again approaches pericentre. This periodicity is visible in the inset of Fig. 6, which zooms in on the time interval between 5.9 and 7.1 yr. The moments of pericentre crossing are indicated for the i = 9° and 69° simulations (dotted vertical lines with matching colours). In agreement with a study of RLOF in eccentric binaries (Lajoie & Sills 2011), there is a substantial delay between the moments of pericentre crossing and the peaks in mass transfer.

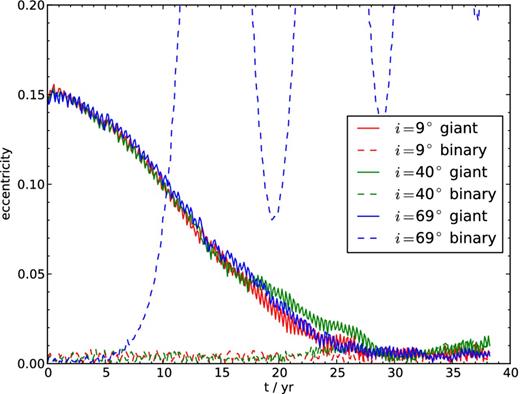
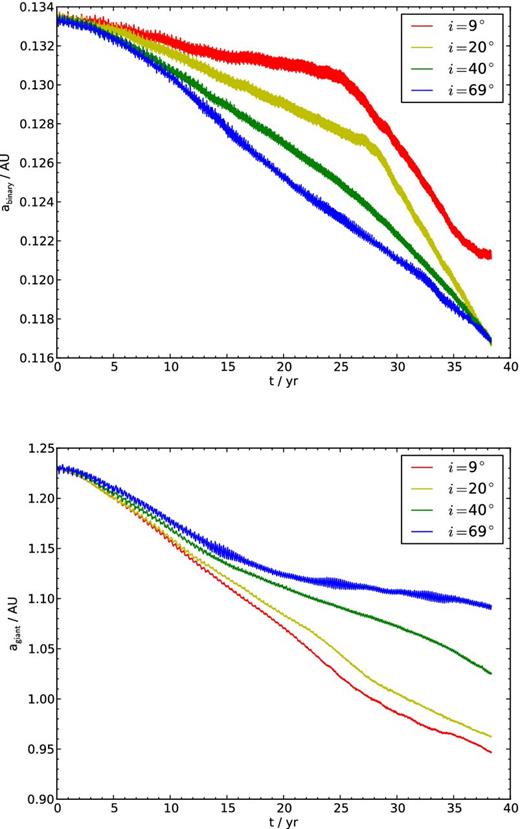
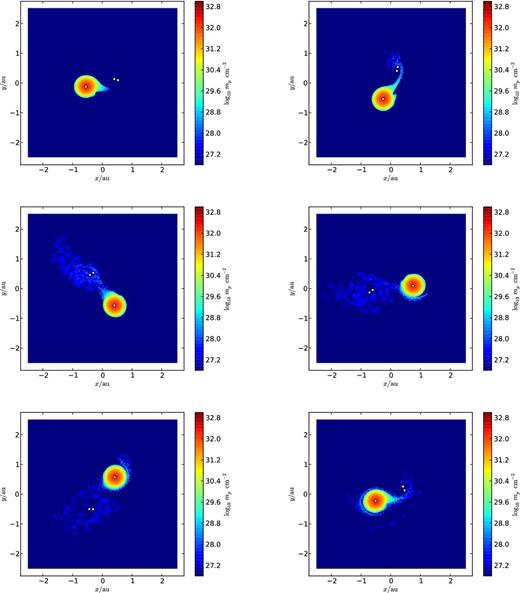
In Fig. 7, we present the evolution of the eccentricity of the inner and outer orbits of ξ Tau, starting from the moment of RLOF. In Fig. 8, we present the evolution of the semimajor axis. The high-inclination (i = 69°) orbit evolves towards a higher inner eccentricity, consistent with the Kozai effect. In itself it is interesting that our combined gravity-hydrodynamics code in amuse reproduces the Kozai effect accurately. We checked this by integrating the three-point-mass simulations using Huayno, which gives a very similar evolution of the eccentricity of the inner orbit. The rate of mass-loss from the giant is lower in the high-inclination orbit. Therefore, the semimajor axis of the outer orbit decreases slower in the highly inclined orbit than in the low-inclination orbit. As a consequence, the rate of mass-loss from the giant becomes even smaller for high inclinations (see Figs 6 and 8). The decay in the eccentricity of the outer orbit (see Fig. 7) is independent of inclination, and is caused by tidal effects in the interaction between the outer giant and the inner binary. The effect of the hydrodynamics on the eccentricity of the inner orbit is negligible. The short periodicity noticeable in Figs 7 and 8 is a reflection of the motion of the inner binary stars. In Fig. 9, we present six column density images of ξ Tau at various times shortly after the onset of RLOF.

Figure 7.

Eccentricity of the outer (drawn lines) and inner (dashed lines) orbit in ξ Tau as a function of time, for an initial relative inclination of i = 9° (red), i = 40° (green) and i = 69° (blue).

Figure 8.

Semimajor axis of the inner (top panel) and outer (bottom panel) orbit in ξ Tau as a function of time, for an initial relative inclination of i = 9° (red), i = 20° (yellow), i = 40° (green) and i = 69° (blue).

The case of HD 97131

The triple HD 97131 is a system in which a 1.5 M_⊙ star orbits a compact (a ≈ 8 R_⊙) binary of 1.29 and 0.90 M_⊙, with an ∼134 d period and an eccentricity of 0.191 (see Table 1). The outer star will start to overfill its Roche lobe at an age of ∼3 Gyr at a radius of 0.26 au, which is consistent with mass transfer case B (Kippenhahn & Weigert 1967; Paczyński 1967). The mass of the star has by that time reduced to 1.48 M_⊙, but like in the case of ξ Tau we did not correct the initial orbital separation for the small amount of mass lost in the stellar wind. Like is the case for ξ Tau, the outer star will fill its Roche lobe, while the two inner binary stars are still on the main sequence and are well detached from their respective Roche lobes.

We agree with Torres et al. (2003) that the inclination of the inner and outer orbits (i₁ = 26° and i₂ = 26°) are suggestive of coplanarity. Therefore, we only performed a simulation with relative inclination i = 0° for HD 97131.

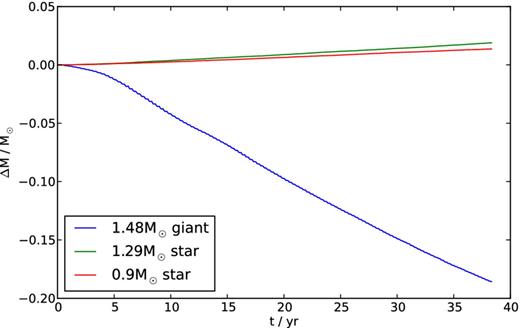
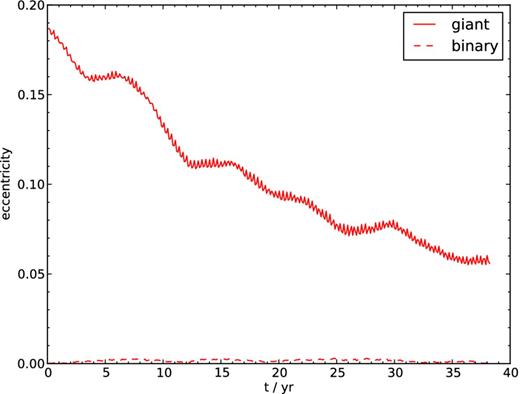
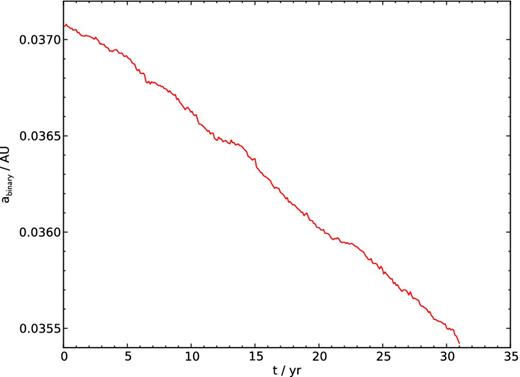
In Fig. 10, we present the evolution of the masses of the three stars. The 1.29 M_⊙ primary (green line) and 0.9 M_⊙ secondary (red line) accrete only a small fraction of the mass lost by the tertiary (blue line). After about 5 years (14 orbits) the mass-transfer rate becomes fairly constant, while the eccentricity of the outer orbit slowly declines (Fig. 11). Both the companion stars accrete about 1 per cent of their own mass from the giant's envelope. The less massive inner star accretes a slightly higher fraction, but in absolute numbers the accretion rate is smaller than that of its more massive companion. The outer star lost 0.19 M_⊙ (13 per cent) of its mass, while the semimajor axes of the inner and outer orbits decreased by 0.42 R_⊙ (5 per cent, see Fig. 12) and 25 R_⊙ (15 per cent, see black solid line in Fig. 13), respectively.

THEORY

Based on our hydrodynamical and gravitational simulations, we can measure the evolution of the orbital parameters and the masses of all three stars. This enables us to constrain some of the fundamental parameters in binary and triple evolution.

To keep the model simple we assume that the mass that is lost from the donor is either accreted on to the inner binary (either the primary star or the secondary) or it is lost from the triple system with a specific amount of angular momentum per unit mass. Upon inspection of our simulation results, no disc forms in either case, but all mass lost by the donor star escapes the triple via the L₂ and L₃ Lagrangian points of the outer orbit. The vast majority of mass lost by the outer star, however, is funnelled through the L₁ Lagrangian point to be ejected by the inner binary system through the L₃ Lagrangian point of the outer orbit. We did not see a circumbinary disc forming, which could be due to the limited resolution near the binary, or the fact that cooling is neglected. However, we do not even expect a circumbinary disc because of the relatively large orbital separation of the inner binary (see Fig. 4).

The evolution of the inner orbit

The mass that flows through the first Lagrangian point of the outer orbit on to the inner binary system can be considered as a gaseous cloud around the binary. The accretion stream intersects with the orbit of the inner binary and this redistributes the mass, angular momentum and energy of the accretion stream. We estimate the minimal distance between the centre of mass of the inner binary and the first periastron passage of the accretion stream using the fitting formula by Lubow & Shu (1975). Following this prescription, the accretion stream of the following systems: HD 57061, HD 108907, HD 21364 (ξ Tau) and HD 203156 intersects with the orbital trajectories of both stars of the inner binary. As a consequence, no disc forms in these systems and the mass dumped from the outer (giant) star on to the inner binary can be considered as some sort of a common envelope, in which the ejection of the matter coming from the outer star is ejected from the inner orbit by its orbital energy. This picture is inspired by the fact that in our calculations the majority of the mass that is provided by the giant is ejected from the inner binary. The amount of giant's material that is accreted by any of the inner stars is fairly small.

We can estimate the binding energy E_b of the material dM that enters the inner binary of mass m_in = m₁ + m₂:

\begin{equation} E_{\rm b} = - {G (m_1 + m_2)\, {\rm d}M \over \lambda a_{\rm in}}. \end{equation}

(2)

Here, λ is some structural parameter that describes the amount of binding energy in the mass that is supplied by the giant. The orbital energy lost due to the ejection of the giant's material is

\begin{equation} E_{{\rm orb}, i} - E_{{\rm orb}, f} = {G m_1 m_2 \over 2a_i} - {G(m_1+dm_1) (m_2+dm_2) \over 2a_f}. \end{equation}

(3)

Like in the classical common-envelope evolution, we can now compare the binding energy of the envelope with the change in binding energy and derive a value of the ratio in energies and the efficiency factor α. Because we do not really know the structure of the common envelope in this case, we keep the two parameters together as αλ, like is proposed by Portegies Zwart & Verbunt (1996).

From the hydrodynamical calculations we now measure all parameters in equations (2) and (3). The results are presented in Table 2, with the name of the simulated triple in column 1, the relative orbital inclination in column 2 and the measured value of αλ in column 3. The presented values of the common-envelope efficiency parameter αλ are averages over about 100 orbits. The error estimates are derived from the temporal variations. The consistency of the result from HD 97131 and the low-inclination simulation of ξ Tau is remarkable, in particular because both systems have quite different parameters. For our simulations with high relative inclination, the measurements of αλ agree with the value derived for an observed post-common-envelope binary with a moderate mass giant (Casewell et al. 2012), and with the value found by high-precision measurements using planets in orbit around a post-common-envelope binary (Portegies Zwart 2013). The simulations with lower relative inclination result in higher values for αλ, which means that it takes less orbital energy from the inner binary to expel the gas. Indeed, when the angular momentum vectors of the inner binary and the inflowing gas are (almost) aligned, less angular momentum needs to be transferred to speed up the gas to the escape velocity.

Table 2.

Averaged values of the common-envelope efficiency parameter αλ over about 100 orbits. The error estimates are derived from the temporal variations. Column 1 gives the name of the simulated triple; column 2 the relative inclination; column 3 the measured value of αλ.

Object name	i	αλ
ξ Tau	9°	5.8 ± 0.8
ξ Tau	20°	5.0 ± 0.6
ξ Tau	40°	3.7 ± 0.3
ξ Tau	69°	2.9 ± 0.3
HD 97131	0°	6.8 ± 0.9

The evolution of the outer orbit

For low-inclination orbits, the evolution of the orbital separation for ξ Tau and HD 97131 is driven by the mass-loss of the donor star during RLOF. During RLOF mass leaving the outer donor star will either be accreted on to the binary stars, form a disc around them or is ejected from the triple system altogether. The orbit will be affected depending on what actually happens to the mass. We can express this in the amount of angular momentum that is carried with the mass that leaves the donor star.

We derive the expression for the effect of mass transfer in the system starting from a binary with primary mass |$m^0_{\rm g}$| and secondary mass |$m^0_{\rm in}$| to the situation after mass transfer with masses m_g and m_in for the primary and secondary stars, respectively. The degree of conservatism is then expressed in the parameter |$f = (m_{\rm g}+m_{\rm in})/(m^0_{\rm g}+m^0_{\rm in})$|⁠. Ignoring internal angular momentum of the outer giant star and the inner binary system, we can express the evolution of the semimajor axis according to the redistribution of mass, which can be expressed as (Huang & Taam 1990):

\begin{eqnarray} {{\dot{a}} \over a} = -2{{\dot{m}}_{\rm g} \over m_{\rm g}} \times \left(1 - \beta {m_{\rm g} \over m_{\rm 2}} - {1 \over 2} {(1-\beta )m_{\rm g} \over m_{\rm g}+m_{\rm 2}} -f {(1-\beta )m_{\rm g} \over m_{\rm g}+m_{\rm 2}} \right). \nonumber\\ \end{eqnarray}

(4)

Here, β is the specific angular momentum of the mass that leaves the system as a fraction of the specific angular momentum of the accreting system (in this case the centre of mass of the inner binary system). Integrating equation (4), assuming that β and the fraction of mass lost f are constant, gives (Portegies Zwart 1995)

\begin{equation} {a \over a_0} = \left( {m_{\rm in} m_{\rm g} \over m_{\rm in}^0 m_{\rm g}^0} \right)^{-2} f^{2\beta + 1}. \end{equation}

(5)

This equation reduces to the classical conservative case

\begin{equation} {a \over a_0} = \left( {m_{\rm g} m_{\rm in} \over m_{\rm in}^0 m_{\rm g}^0} \right)^{-2} \end{equation}

(6)

when we adopt f = 1, in which case the evolution of the orbital separation becomes independent of β.

The specific angular momentum of the mass that leaves the system is uncertain. We can measure the amount of angular momentum lost from the system by applying conservation of angular momentum in the non-conservative case, like for binaries was discussed by Portegies Zwart (1995).

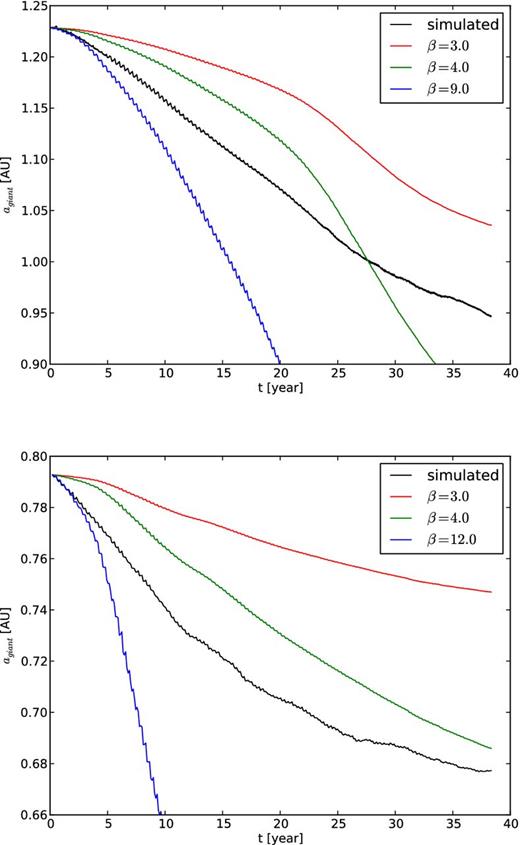
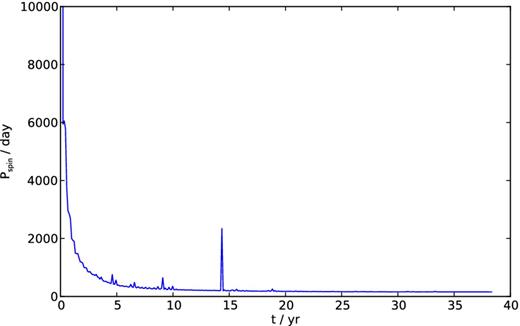
In Fig. 13, we present the orbital evolution of ξ Tau and HD 97131 (solid black curves). The coloured curves give the results of equation (5) with comparable models, adopting values for β of 3 (red curve), 4 (green curve), and 9 and 12 for ξ Tau and HD 97131, respectively (blue curve). The models with lower values for β do not match the simulations very well in the beginning, but we argue that this is because the giant's orbit and spin are not yet in corotation. The time-scale on which the giant gets into corotation is similar to the time-scale at which the models with lower β values start to match the slope of the orbital evolution, as can be seen by comparing Figs 13 and 14. After about 35 years the evolution of the semimajor axis of both ξ Tau and HD 97131 matches the model with β ≃ 3.

THE FUTURE OF ξ TAU AND HD 97131

The future of ξ Tau

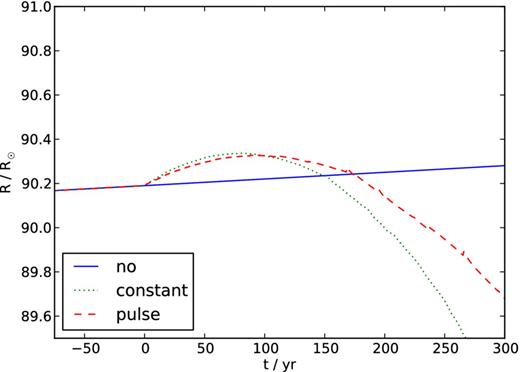
At the start of our hydrodynamics simulations the outer star has a radius of ∼90 R_⊙ and due to evolution it continues to grow at a rate of about 0.0004 R_⊙ yr⁻¹. With the observed orbital parameters the size of the Roche lobe is ∼82 and ∼111 R_⊙ at pericentre and apocentre, respectively, which means that the star at pericentre overfills its Roche lobe but at apocentre is detached. The outer orbit will quickly circularize. By that time the separation decreased to 1.0 au for low initial inclination angles. The size of the Roche lobe at that moment will be about 78 R_⊙, and naively speaking the star will continuously be filling its Roche lobe. However, the mass-loss causes the giant to shrink at an accelerated rate and in about 300 years after the onset of mass transfer it detaches from its Roche lobe. In Fig. 15, we present the evolution of the size of the outer star as calculated by mesa for different mass-loss schemes. The blue drawn line shows the radius evolution with no mass-loss, for comparison. The green dotted line shows the radius evolution when the star loses mass at a constant rate. The red dashed line corresponds to the ‘pulsing’ mass-loss for eccentric orbits we see in our simulations, with no mass-loss for 80 per cent of the orbit, and for 20 per cent of the orbit a mass-loss five times higher compared to the constant mass-loss scheme. We realize that when the radius drops significantly, the giant will detach from its Roche lobe and the radius evolution will continue the normal stellar evolution track (no mass-loss), until RLOF is re-established. This will result in a radius evolution with a series of bumps like the one in Fig. 15.

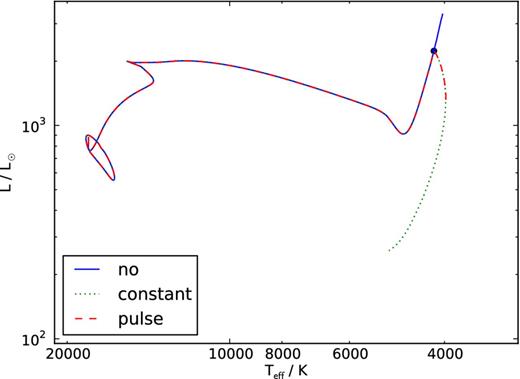
In Fig. 16, we present the Hertzsprung–Russel diagram for ξ Tau. The mass-loss causes the outer star to drop in magnitude and become first red and later blue, below the giant branch but to the right of the main sequence. The extraordinary location of the star in the Hertzsprung–Russel diagram would place it where some of the sub-subgiants reside (Mathieu et al. 2003). This position in the Hertzsprung–Russel diagram is consistent with several sub-subgiants or red stragglers² found in NGC 6791 (in particular star nos. V9, V17 and V76) (Kaluzny 2003), which in their interpretation are variable stars. Similar objects have also been found in NGC 6752 (Rubenstein & Bailyn 1997), 47Tuc (Albrow et al. 2001) and M67 (Mathieu et al. 2000, 2003) (S1036 and S1113). The red stragglers in M67 and V9 in NGC 6791 are confirmed binaries, and it cannot be excluded that the others have an unseen binary companion. The argument for the donor in the binary in our calculation to become a sub-subgiant is consistent with the explanation given earlier (van den Berg, Verbunt & Mathieu 1999).

During the first half of the simulation, the outer orbit quickly circularizes and the giant's orbit and spin are driven into corotation. Subsequently, for low-inclination angles, the rate of change of the inner binary semimajor axis steepens significantly, while the evolution of the outer orbit slightly flattens off (see Figs 7 and 8). For example, for an initial inclination of i = 9°, the outer star loses 0.69 M_⊙ (15 per cent) of its mass during the past 10 years of the simulation, while the semimajor axes of the inner and outer orbits decreased by 1.3 R_⊙ (4.9 per cent) and 10 R_⊙ (4.7 per cent), respectively. Since the ratio of the fractional rates of change of the inner and outer semimajor axes is approximately unity,

\begin{equation*} {(\dot{a}_{{\rm in}} / a_{{\rm in}}) \over (\dot{a}_{\rm out} / a_{\rm out})} \simeq 1, \end{equation*}

the triple remains dynamically stable. The system as a whole shrinks significantly during the RLOF phase, but not enough to initiate RLOF in the inner binary.

After the outer star has turned into a white dwarf, the inner binary will eventually acquire Roche lobe contact and an entirely new phase in the evolution of the triple starts. We will not dwell on the further evolution of the system, but the intermediate phase where a white dwarf has a circular orbit around a close (also circularized) binary could be interesting from an observational point of view.

The future of HD 97131

RLOF in HD 97131 sets in around 3 Gyr when the 1.5 M_⊙ donor has grown to a 56 R_⊙ giant. Upon the initial Roche lobe contact the accretion stream of the donor arrives at a distance of ∼6.2 R_⊙ from the centre of mass of the inner binary, i.e. it comes within the orbit of the inner binary (which has an orbital separation of about 8 R_⊙). The absence of an accretion disc in this system is then not a surprise.

Initially, the outer orbit shrinks faster than the inner orbit, with a low ratio of the rates of change of the inner and outer semimajor axes

\begin{equation*} {(\dot{a}_{{\rm in}} / a_{{\rm in}}) \over (\dot{a}_{\rm out} / a_{\rm out})} \simeq 0.3. \end{equation*}

While circularizing, this ratio approaches unity, similar to the value found for ξ Tau. In this case, however, the initial semimajor axis of the inner orbit is already very small, and the inner binary can possibly initiate RLOF.

DISCUSSION AND CONCLUSIONS

We performed a series of simulations using the amuse software environment in order to study the gravitational dynamics, hydrodynamics and stellar evolution of hierarchical triple systems. In the triples we selected, the outer star is sufficiently massive and the outer orbit sufficiently small for RLOF from the outer star on to the inner binary to occur. These systems are relatively rare ≲1 per cent (6/725 in the catalogue), but the consequences of this RLOF phase can be profound.

We follow the onset of RLOF for two cases in detail for a few decades using a combination of codes. We used a gravitational N-body code to follow the dynamical evolution of the three stars, an SPH code to study the accretion stream from the outer star on to the inner binary system and a stellar evolution code to continue the evolution of the outer Roche lobe filling star.

In neither of the cases we studied an accretion disc formed, not even a circumbinary disc. The mass that leaves the outer star is funnelled through the first Lagrangian point of the outer orbit to land very near the inner binary system. The interaction between the gas and the inner binary causes the former to be ejected from the binary system like in a common envelope. For systems with a high relative inclination, the evolution of the inner binary is adequately described by the common-envelope prescription with an efficiency parameter αλ ≃ 3, which is consistent with the values derived for observed post-common-envelope binaries (Casewell et al. 2012; Portegies Zwart 2013). Simulations with lower relative inclination result in higher values for αλ, which is expected since the angular momentum vectors of the inner binary and the inflowing gas are aligned, and less angular momentum needs to be transferred to speed up the gas to the escape velocity. For the mass-loss from the outer binary system we measure a value of β ≃ 3–4, which means that the mass lost from the binary carries less angular momentum per unit mass compared to that is available in the second Lagrangian point. However, also here the values of both systems studied in detail give a consistent result.

The rapid mass-loss causes the outer giant to shrink and it may even detach from its Roche lobe, which temporarily would interrupt the mass transfer. The orbital separation of the inner binary therefore shrinks in time until the inner binary will itself engage in a phase of RLOF or the envelope of the outer star is depleted.

In one of our studied cases, ξ Tau, the mass transfer causes the inner and outer orbits to shrink at the same fractional rate,

\begin{equation*} {(\dot{a}_{{\rm in}} / a_{{\rm in}}) \over (\dot{a}_{\rm out} / a_{\rm out})} \simeq 1, \end{equation*}

and this system is therefore likely to remain dynamically stable, while the entire envelope of the outer star is transferred to the inner binary. After the main-sequence phase of the inner binary stars, a common-envelope phase with all three stars embedded is likely to result in a collision between all three stars, although we did not explicitly test this hypothesis.

In the other case, of HD 97131, the ratio of the rates of change of the inner and outer semimajor axes also approaches unity, and initially the triple is dynamically stable as well. However, the inner binary is much more compact in this system, and the decrease in semimajor axis can possibly lead to simultaneous RLOF in the inner binary.

In both cases the detailed evolution, for as long as we followed it hydrodynamically, resulted in systems that have interesting observational implications. The phase we followed, however, is very short. The chance of observing the mass transfer in action is therefore rather small. The long-term effects, however, are more likely to be observable. A merger between a giant and two main-sequence stars could lead to some sort of curious stellar object with non-canonical atmospheric and spectral features, but also the white dwarf in a circular orbit around a tight binary would be an interesting finding.

Although our theoretical analysis is limited in scope and detail, we would like to point out, and we are not to first to say this, that the evolution of triples is quite complicated, and not a simple extension of binary evolution with some third component. The mutual interaction in terms of hydrodynamics, stellar evolution and the dynamical complications makes for a challenging topic to study, and very hard to get a general consensus on triple evolution.

It is a pleasure to thank Adrian Hamers, Edward P. J. van den Heuvel, Inti Pelupessy, Arjen van Elteren and the anonymous referee for comments on the manuscript and discussions. This work was supported by the Netherlands Research Council NWO (grant nos. 612.071.305 [LGM], 639.073.803 [VICI] and 614.061.608 [amuse]) and by the Netherlands Research School for Astronomy (NOVA). We made use of pynbody (http://code.google.com/p/pynbody) for generating the column density images (Fig. 9) in this paper.

Figure 9.

Column density images of ξ Tau after 76, 92, 116, 148, 172 and 224 d (from left to right and from top to bottom) since the onset of RLOF.

Figure 10.

Mass of each component of HD 97131, as a function of time, starting at the onset of RLOF.

Figure 11.

Eccentricity evolution of the inner (dashed line) and outer (drawn line) orbit of HD 97131.

Figure 12.

Semimajor axis evolution of the inner orbit of HD 97131.

Figure 13.

Semimajor axis as a function of time for ξ Tau (top panel) and HD 97131 (bottom panel). The black solid curve gives the actual calculated evolution using the simulations from Section 4. The coloured curves give the orbital separation as a function of time using equation (5) for different values of β.

Figure 14.

Evolution of the spin period of the outer star as a function of time for HD 97131.

Figure 15.

Evolution of the size of the tertiary star in ξ Tau starting from the moment of the RLOF phase (t = 0). In the first millennium after the onset of RLOF, the star grows quite dramatically to eventually drop.

Figure 16.

Hertzsprung–Russel diagram of the tertiary star in ξ Tau. The evolution of the ZAMS star starts at the lower-left corner, and the star evolves through a series of evolutionary phases until it reaches RLOF near the tip of the AGB (indicated with a bullet). During the RLOF phase the star loses mass in episodes which causes the evolution to be quenched, as indicated in the track to the bottom right after the bullet point.

1

http://www.amusecode.org

2

It is interesting to note that in each of the papers that classify ‘red stragglers’ the authors make the claim that they coin the term. The earliest mention of the term that we could find was in Foy & Proust (1981).