Search for wormhole candidates in active galactic nuclei: radiation from colliding accreting flows

ABSTRACT

The underlying hypothesis of this work is that the active galactic nuclei (AGNs) are wormhole mouths rather than supermassive black holes. Under some – quite general – assumptions such wormholes may emit gamma radiation as a result of a collision of accreting flows inside the wormholes. This radiation has a distinctive spectrum much different from those of jets or accretion discs of AGNs. An observation of such radiation would serve as evidence of the existence of wormholes.

accretion, accretion discs, black hole physics, galaxies: active, galaxies: nuclei, galaxies: Seyfert, gamma-rays: galaxies

1 INTRODUCTION

According to an interesting recent hypothesis, active galactic nuclei (AGNs) are not supermassive black holes (SMBHs), but rather mouths of primordial macroscopic wormholes (Kardashev, Novikov & Shatskiy 2007; Bambi 2013; Li & Bambi 2014; Zhou et al. 2016). In this paper, we show that the validity of such a hypothesis may have observable consequences.

2 MODEL AND BASIC EQUATIONS

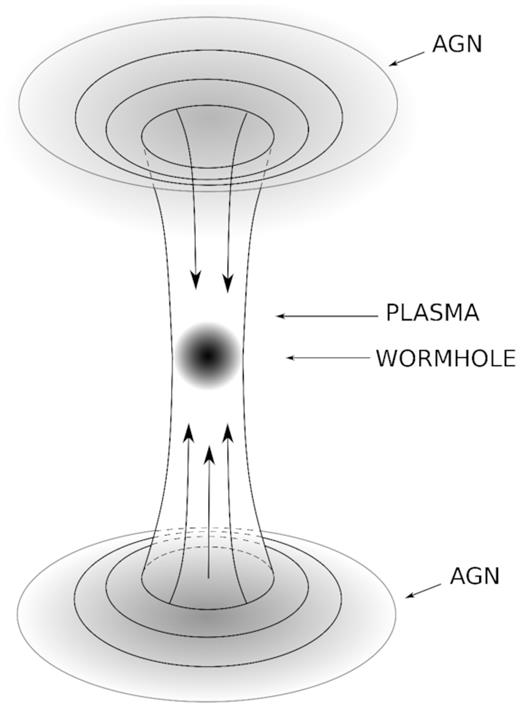
Consider a traversable wormhole connecting two galactic centres (see Fig. 1). To make the situation as simple as possible, assume that the wormhole is spherically symmetric, static, and empty everywhere beyond a spherical layer L. Assume further that the gravitational force acting on a radially falling test particle in any point of that wormhole is directed towards the throat.

Figure 1.

Traversable wormhole connecting two AGNs.

An example of a wormhole satisfying all these requirements is a ‘Schwarzschild-like wormhole’

$$\begin{eqnarray*} \mathrm{d}s^2 =-e^{2 h(l)}c^2\mathrm{d}t^2 + \mathrm{d}l^2 + r^2(l) (\mathrm{d}\theta ^2 +\sin ^2 \theta \, \mathrm{d}\phi ^2), \, l\in \mathrm{I\!R}, \end{eqnarray*}$$

(1)

studied in its capacity as a particle accelerator in Krasnikov (2018). c in (1) is the speed of light, l is (up to the sign) the proper radial distance from the wormhole’s throat (Morris & Thorne 1988), and r(l) and h(l) are smooth even functions monotone increasing at positive l (almost all these conditions may be weakened, but we consistently keep avoiding unnecessary complications) and obeying the following relations:

$$\begin{eqnarray*} \mathrm{d}r = \sqrt{ 1-1/x}\, \mathrm{d}l, \qquad x\equiv r/r(0), \end{eqnarray*}$$

(2)

$$\begin{eqnarray*} h(x)|_{r\gt r_*}=\tfrac{1}{2}\ln (1-1/x), \end{eqnarray*}$$

(3)

where r_* is some constant greater than r(0). We choose this constant to be close to the radius of the wormhole’s throat

$$\begin{eqnarray*} 2r(0) \gt r_* \gt r(0), \end{eqnarray*}$$

(4)

i.e. the wormhole is required to be short (again, this condition might be dropped and r_* be made a free parameter of the model, but we do not need such generality, while the hypothesis 4 will be helpful for the subsequent calculations). Thus, for all r > r_* the metric (1) is that of Schwarzschild with mass

$$\begin{eqnarray*} M\equiv \frac{c^2}{2G}r(0)\approx \frac{c^2}{2G}r_*. \end{eqnarray*}$$

(5)

At smaller r, the shape of h(l) [not of r(l)] differs from its Schwarzschild counterpart h_Sch, i.e. from |$\tfrac{1}{2}\ln (1-1/x)$|⁠, which means that this region is non-empty (it is, in fact, the layer L mentioned above). As shown in Morris & Thorne (1988), if the Einstein equations hold, the matter filling L unavoidably is exotic, i.e. its energy density as measured by some observers in some points (including the points of the sphere l = 0) is negative. There are several proposals in the literature on what could serve as exotic matter, see e.g. Lobo (2017) and Visser (1995) for a review, but in this paper we shall not consider them (for lack of need: as long as the matter supporting the wormhole does not interact electromagnetically, its nature is irrelevant). Two remarks, however, are in order:

1. The idea that the Einstein equations require exotic matter to have T_tt < 0 and a Schwarzschild-like wormhole to have M < 0 is oversimplification. In particular, the wormhole (1) has T_tt = 0 and M > 0 (Krasnikov 2018). This can be seen from equation 12 in Morris & Thorne (1988) given that the function b appearing there is constant in our case.

2. As ‘normal’ matter – with the stress-energy tensor t_μν accretes to a wormhole (in such a manner that t_μν remains diagonal in the coordinate basis), the matter inside the latter presumably becomes ‘less and less exotic’ (assuming that the stress-energy tensor near the throat is the sum T_μν + t_μν, which is justified by our condition that the two kinds of matter do not directly interact). Consequently, in some time |$\mathcal {T}_\text{stab}$| the components of t_μν may cease to be negligible and the wormhole may lose stability and collapse. Unfortunately, for the reasons discussed in the previous item, it is hard to find an estimate on |$\mathcal {T}_\text{stab}$| valid for all types of wormhole.

The most important difference between h_Sch and h is that the latter, in contrast to the former, is bounded. That is to say the spacetime (1) is a wormhole rather than a black hole. It has no horizon and is therefore traversable (Morris & Thorne 1988). This fact makes it possible to use a Schwarzschild-like wormhole as super accelerator. Indeed, the matter attracted by mouths of such a wormhole will form two fluxes colliding at the throat. To analyse this process, consider, first, a particle of mass μ that falls freely from infinity (with zero initial velocity) and in the throat of the wormhole (1) hits head-on exactly the same oncoming particle. The energy of this collision (in the centre-of-mass system) is, see equation 12 in Krasnikov (2018),

$$\begin{eqnarray*} E_{\rm c.m.} &=& 2 \mu c^2\Gamma [1+\mathcal {O}(\Gamma ^{-2})],\\ \Gamma &\equiv& c \max \Bigl (|g_{tt}|^{-1/2}\Bigr) =e^{-h _\text{min}}, \end{eqnarray*}$$

(6)

where g_tt is the corresponding component of the metric (1). Note that the function h attains its minimal value h_min at the throat l = 0. So, h(0) is the only wormhole’s characteristic on which E_c.m. depends. Though h(0) is fixed for any given wormhole, one may call the Schwarzschild-like wormhole a super accelerator, because that fixed value can be arbitrarily high.

As a result of the pair collisions discussed above, an observer watching the wormhole will see two spheres (these are the spheres with radii r_* bounding L) of ultrarelativistic plasma. These spheres radiate with a distinctive spectrum, see bellow, much different from those of jets or accretion discs, which makes it possible to identify the wormhole.

3 ESTIMATES

3.1 Assumptions

The phenomenon in discussion is rather complex and to explore it we will make as much simplifying assumptions as possible. Specifically, we consider a pair of AGNs with the masses M ≈ 5 × 10⁸ M_⊙ connected by a Schwarzschild-like wormhole (1). We assume that

• the galaxies in question are Narrow-line Seyfert 1 Galaxies (NLS1) (Madejski & Sikora 2016; Baghmanyan & Sahakyan 2018; Kynoch et al. 2019; Paliya et al. 2019), which have a fairly weak gamma radiation, so our supposed wormhole (WH) gamma radiation will be less diluted;

• the plasma layer is heated (only) by the collision of the fluxes;

• the magnetic field, the interaction of the infalling matter with the outcoming radiation, and the backreaction of the spheres on the metric of the wormhole are negligible.

Now we can roughly estimate plasma temperature and spectrum.

3.2 Plasma parameters

The characteristic accretion rates of NLS1 lie (Bian & Zhao 2003; Collin & Kawaguchi 2004) within the range of

$$\begin{eqnarray*} \dot{m} \approx 0.1 - 1 \,\mathrm{ M}_{\odot }\, \textrm {yr}^{ -1}. \end{eqnarray*}$$

(7)

According to estimates of duty cycles of AGNs of this type (Shankar, Weinberg & Miralda-Escudé 2013; Aversa et al. 2015; Tucci & Volonteri 2017), this accretion regime should exist for at least 10⁸ yr. So, the mass of the plasma spherical layer is at least

$$\begin{eqnarray*} m \approx 10^8\, \mathrm{ M}_{\odot }, \end{eqnarray*}$$

(8)

where the layer’s mass m is understood as the integral of density rather than a characteristic of the wormhole’s metric.

Now let us estimate the proton concentration in the accreting plasma. To that end assume (following Bian & Zhao 2003; Collin & Kawaguchi 2004) that the region external to a sphere r = const ≫ r_* is left by M_⊙ of matter in a year. Then (since the matter does not accumulate between that sphere and the sphere r = r_*) the latter will be left by exactly the same amount of plasma every year of the coordinate time t. This plasma moving with (almost) the speed of light, will fill the layer of proper (with respect to an observer whose r-, ϕ-, and θ-coordinates are constant) volume |$V_\text{prop} =4\pi r_*^2 \cdot \sqrt{-g_{tt}(r_*)}\cdot 1\,$|ly. So, the proton concentration is

$$\begin{eqnarray*} n_{\mathrm{ acc}} &=& N/V_\text{prop}\approx M_{\odot }\Gamma / \left(m_\mathrm{ p} 4\pi r_*^2 \times 1\, \mathrm{ly}\right) \\ &\approx& \frac{\Gamma }{(M/\mathrm{ M}_{\odot })^2} \frac{M_{\odot }}{ m_\mathrm{ p}} \frac{1}{\pi \, (10^{11}\, \mathrm{cm}^2)\times (1\, \mathrm{ly})} \\ &\approx& \frac{\Gamma }{ (M/\mathrm{ M}_{\odot })^2} \frac{2\times 10^{30}}{ 1.7 \times 10^{-27}} \frac{10^{-18}\, \mathrm{cm}^{-1} }{\pi \, (10^{11}\, \mathrm{cm}^2) } \\ &\approx& \frac{\Gamma }{ (M/\mathrm{ M}_{\odot })^2}\times 4\times 10^{27}\, \mathrm{cm}^{-3} , \end{eqnarray*}$$

(9)

where m_p is the proton mass and N is the number of protons in V_prop.

If we take an AGN mass value of M ≈ 5 × 10⁸ M_⊙ and Γ ≈ 10, then |$n_{\mathrm{ acc}} \approx 1.6\times 10^{11}\, \mathrm{ cm}^{-3}$|⁠.

3.3 Temperature and spectrum

By equation (6), the temperature T of the plasma cloud is approximately

$$\begin{eqnarray*} T \approx \Gamma m_\mathrm{ p} c^2 / k \approx 10^{13} \Gamma \, \mathrm{ K}, \end{eqnarray*}$$

(10)

where m_p is the proton mass and k is the Boltzmann constant.

The plasma with such a temperature and proton concentration was considered, for example, in Marscher, Vestrand & Scott (1980). So in what follows we will use their results.

3.3.1 Spectral peak

At such high temperatures in the plasma the production of π⁰ mesons begins (Kolykhalov & Syunyaev 1979; Marscher et al. 1980; Dermer 1986). π⁰ mesons decay into two photons with energies ∼68 MeV. For T = 2.5 × 10¹³ K and T = 10¹⁴ K the gamma-ray production spectra of plasma for this radiation mechanism (in Minkowski space) were found in Marscher et al. (1980). The latter spectrum has a peak value of |$Q_\text{max} \approx 10^{-13.4}\, \mathrm{ erg}\, \mathrm{ cm}^{-3}\, \mathrm{ s}^{-1}$| at about 68 MeV, where Q is the gamma-ray production value. To find the spectrum of the wormhole (as measured by an observer resting out of the wormhole), we extrapolate Marscher’s result (fig. 3 from Marscher et al. 1980) and assume that the peak value in the spectrum is reached at |$\sim 68 \Gamma ^{-1} \,$|MeV (the factor Γ⁻¹ is due to the red shift experienced by a photon on its way from the throat to infinity) and equal to Q_max(T) ≈ Q_max(T = 10¹⁴ K)(T/10¹⁴ K)^0.25/Γ.

3.3.2 Observability

In order to evaluate possible observed flux value of plasma cloud we will use the relation (Marscher et al. 1980):

$$\begin{eqnarray*} F(E_\gamma) = \frac{V}{4\pi D^2} Q(E_\gamma), \end{eqnarray*}$$

(11)

where E_γ is the photon energy, F is the flux value, V is the total volume of the plasma cloud, and D is the distance to the observer.

In order to obtain peak flux value comparable in order of magnitude to observed values for NLS1 (⁠|$\sim 10^{-13}\, \mathrm{ erg}\, \mathrm{ cm}^{-2}\, \mathrm{ s}^{-1}$|⁠) using equation (11), we have to assume that V/(4πD²) ≥ 0.1cm. Characteristic distance for observed AGNs of this type is about 10⁹ light-years or ∼10²⁷ cm, so the volume of the radiating plasma must be at least 10⁵⁴ cm³. In Marscher et al. (1980) the plasma is optically thin, so we consider radiation only from outer layers of plasma cloud with a volume of 10 per cent of the total volume of cloud. Thus full cloud volume will be ∼10⁵⁵ cm³. Taking into account (9) we obtain the mass of the plasma cloud

$$\begin{eqnarray*} m = n_{\mathrm{ acc}}m_\mathrm{ p}V \approx 2.4 \times 10^{38}\, \mathrm{ kg} \sim 10^8\, \mathrm{ M}_{\odot } . \end{eqnarray*}$$

(12)

Comparing this with characteristic mass of accreted matter for NLS1 10⁸ M_⊙ (8), we see that the NLS1 observed accretion rate 0.1−1 M_⊙ yr⁻¹ (7) is sufficiently high for WH radiation to be observable.

The resulting spectrum for |$V/(4\pi D^2) \approx 0.1\, \mathrm{ cm}$| (11) looks (qualitatively) as shown in Fig. 2.

Figure 2.

The spectrum of the ultrarelativistic plasma [for |$V/(4\pi D^2) \approx 0.1\, \mathrm{ cm}$| (11)] for Minkowski case (Γ = 1) and for wormhole case (⁠|$\Gamma = 10,\, 100$|⁠).

4 CONCLUSIONS

We can conclude that a peak at about |$68 \Gamma ^{-1} \,$|MeV should appear on the AGN spectrum. It should be emphasized that this peak in the spectrum can be quite high (⁠|$\sim 10^{-13}\, \mathrm{ erg}\, \mathrm{ cm}^{-2}\, \mathrm{ s}^{-1}$|⁠), comparable to flux value of jet radiation of NLS1.

ACKNOWLEDGEMENTS

SK is grateful to RFBR for financial support under grant no. 18-02-00461 ‘Rotating black holes as the sources of particles with high energy’.

DATA AVAILABILITY

The data underlying this article are available in the article.