-
PDF
- Split View
-
Views
-
Cite
Cite
Hiroshi Tanaka, Soichi Ogishima, Network biology approach to epithelial–mesenchymal transition in cancer metastasis: three stage theory, Journal of Molecular Cell Biology, Volume 7, Issue 3, June 2015, Pages 253–266, https://doi.org/10.1093/jmcb/mjv035
Close - Share Icon Share
Abstract
Epithelial–mesenchymal transition (EMT) plays a critical role in promoting cancer metastasis. In this study, cancer EMT is considered as an overall structural change in the gene regulatory network (GRN), and its essential features are elucidated by the network biology approach. We first defined the state space of GRN as a set of all possible activation patterns of GRN, and then introduced the quasi-potential field into this space to show the relative stability distribution of each state. The quasi-potential was determined empirically by collecting gene expression profiles from public databases. Changes of GRN states during the EMT process were traced in the state space, by using time-course data of gene expression profiles of a cell line inducing EMT from the database. It was found that cancer EMT occurred in three sequential stable stages, each of which formed a potential basin along the EMT trajectory. As confirmation, structural changes of GRN were estimated by applying the ARACNe algorithm to the same time-course data, and then applying master regulator analysis to extract the main regulations. Each group of master regulators was found to be alternatively active in the subsequent three stages to cause overall structural changes of GRN during cancer EMT.
Introduction
The epithelial–mesenchymal transition (EMT) is a molecular program through which an epithelial cell loses its intercellular adhesion and acquires a migratory mesenchymal phenotype (Boyer and Thiery, 1993; Hay, 1995). During EMT, fixed, polarized epithelial cells, which are connected laterally via cellular junctions, dissolve the junctions and convert into individual, non-polarized, motile mesenchymal cells. The primary function of EMT is well-known as a necessary step in development such as mesoderm formation (gastrulation) and neural crest delamination during embryogenesis as well as wound healing in adulthood.
With accumulating evidence, EMT has now been widely acknowledged as a critical step in promoting metastasis in epithelium-derived carcinoma (Thiery, 2002; Kalluri and Weinberg, 2009). Cancer metastasis is known to cause of about 90% of human cancer deaths. Hence, one of the major challenges of cancer research is to elucidate the mechanism of metastasis in order to eradicate it. Thus, studies on the EMT process in cancer are now attracting wide interest and have been advancing remarkably in recent years.
Despite rapid increases in detailed knowledge about cancer EMT, however, we have not yet understood the essential nature of cancer EMT, nor have we found an appropriate approach to draw a whole picture of the cancer EMT process. In this study, we tried to clarify the essence of cancer EMT process by the network biology approach. We consider that the cancer EMT process is not just an incidental aberration of the cellular process, but a biologically deep, overall structural change in the gene regulatory network (hereinafter gene network or GRN) in promoting cancer metastasis. Hence, a dynamical network approach is most appropriate to grasp the essential features of cancer EMT.
To conduct investigations on EMT from this point of view, we first defined ‘state space of the gene network’ (hereinafter GRN space), which comprises all possible activation patterns of the gene network, as a basic framework to deal with its temporally varying activity. Then, we introduced a quasi-potential distribution into this GRN space to indicate the relative stability of each state in the GRN space. In doing so, we referred to the concept of Waddington's epigenetic landscape (hereinafter Waddington's landscape) (Waddington, 1957). Waddington proposed an epigenetic landscape as a metaphor for a developmental process where a ball (cell) is rolling down a series of branching valleys separated by ridges on an inclined surface. Waddington's landscape is considered as a quasi-potential distribution defined on all the cell states, where the elevation of the potential surface is inversely related to the likelihood of occurrence of the corresponding cell state. Waddington's landscape had been considered as just a metaphor without physical evidence, but recently Huang et al. (2009) and Wang et al. (2014) have proposed a mathematical quasi-potential model to quantify Waddington's landscape for a gene network regulating cell fate.
In this study, we proposed a new method to create Waddington's landscape quantitatively, which is essentially empirical and different from the previous studies. We collected a number of samples of gene expression profiles, each of which shows a particular GRN activation pattern, from public databases of gene expression profiles, such as GEO (Gene Expression Omnibus) (Barrett et al., 2009) of NCBI (National Center for Biotechnological Information) or ArrayExpress of EBI (European Bioinformatics Institute) (Brazma et al., 2003). By using collected samples, we calculated an empirical frequency distribution (denoted by φ) of GRN states. The quasi-potential (denoted by ψ) is then obtained by applying a negative logarithm transformation to this empirical frequency distribution, if we assume that the Boltzmann formula: ψ = −k log φ (k: const.) is applicable to the GRN space. We consider the quasi-potential distribution on GRN space (hereinafter GRN-space landscape) thus obtained to be the same as a quantified Waddington's epigenetic landscape.
Terminally differentiated cell types stay in stable cellular states to form basins within this potential field. The cancer EMT process is considered to draw a trajectory in this GRN space; starting from a basin of epithelial cell states, climbing over a separating ridge or ‘epigenetic barrier’, and then falling down to a basin of mesenchymal cell states. We depicted this EMT movement, by utilizing the time-course data of gene expression profiles during EMT reported by Takahashi et al. (2010), where they used a cell line of retina pigment epithelial cells, which induces EMT in response to treatment with TGF-β and TNF-α. We traced the state movement of EMT in the GRN space and found that the cancer EMT process undergoes three sequential stable stages, each of which forms a potential basin along the EMT trajectory.
To confirm the three-staged transition of cancer EMT, we estimated structural changes of the gene network during cancer EMT from the gene expression profile data. We again used the same time-course data of EMT reported by Takahashi et al., and applied the ARACNe (Algorithm for the Reconstruction of Accurate Cellular Networks) algorithm by Margolin et al. (2006), which is one of the well-used methods for interring the gene network from the gene expression profile data. The result of inference by ARACNe was, however, rather complex to interpret. Therefore, we applied the master regulator analysis (Carro et al., 2010) to this gene network estimated by ARACNe, to identify the main regulations conducted by master regulators of the gene network, which significantly controls differentially expressed genes along the time-course of EMT. The main structures of the estimated gene network during EMT were investigated by each group of major master regulators, which are alternatively active in subsequent time spans to cause the large-scale structural changes of GRN during cancer EMT.
Results
Creation of GRN space and calculation of statistical and quasi-potential distribution in GRN space
Definition of the state space of the gene network (GRN space)
A state space representation was introduced as a basis for the study in order to deal with temporally varying activity of the gene network. Wired structure of the gene network is innately coded in the congenital genome, such that it is the same in all cells of the body, but activation patterns (expressed genes and activated interactions between genes) of the gene network differ among cell types. We defined a state space as a set of all the activation patterns of a gene network, denoted as GRN space. Actually each state of the gene network (a unique point in this GRN space) is represented by a particular gene expression profile corresponding to that state, so that GRN space is considered to be substantially the same as a whole set of gene expression profiles. GRN space is a multi-dimensional space where the number of its dimensions is equal to the total number of genes for gene expression profiles.
Collection of gene expression profiles of the epithelial and mesenchymal cell states
We introduced a statistical distribution (φ) of cell states into GRN space, especially that of epithelial and mesenchymal cell types. To do this, we empirically collected a large number of gene expression profiles of the epithelium and mesenchyme from GEO and ArrayExpress. We carefully extracted gene expression profiles of these two cell types and obtained 14 datasets (13 datasets from GEO and 1 dataset from ArrayExpress, see Materials and methods and Supplementary Table S1).
In addition to these datasets, time-course gene expression profiles during the cancer EMT process, which were observed by Takahashi et al. were included for use in later analyses of cancer EMT process. Experimental data by Takahashi et al. were obtained by using a human retinal pigment epithelium (RPE) cell line (ARPE-19) that induces cancer EMT in response to the combined treatment of TGF-β and TNF-α. In Takahashi et al.'s experiment, total RNA was extracted and gene expression profiles were measured at six time points from the start of the treatment with TGF-β and TNF-α, to 60 h after that. We used Takahashi et al.'s data at the start for epithelial states and those at 60 h after the start for mesenchymal states.
Selection of the genes for the subspace coordinates
In creating a statistical distribution in the GRN space in the vicinity of epithelial and mesenchymal cell states, a full dimensioned GRN space was not used, but it was projected onto a specific subspace where distributions of epithelial and mesenchymal states could be sufficiently and clearly separated. To explore this specific GRN subspace, we selected a set of coordinate variables (genes), whose expression profiles differ significantly between the epithelial and mesenchymal cell states (significance level, P = 0.1 × 10−5). Following the procedure described in Materials and methods, we obtained specific coordinates (genes) for this GRN subspace, the dimension of which was sixty one (gene name/IDs, probe IDs, medians of gene expression and descriptions by NCBI GENE are shown in Supplementary Table S1).
Principal components used for depiction of statistical distribution of epithelial and mesenchymal states
To draw a three-dimensional view of the statistical distribution of epithelial and mesenchymal states, we applied the principal component analysis (PCA) to this GRN subspace comprising of 61 genes. The first and second components were used as the x-y axis, and the statistical distribution was drawn on this two-dimensional plane along the direction of the z axis.
For interpretation of meanings of the obtained principal components, the genes with the top 20 highest principal component loadings are listed in Table 1 for the first and second components. As shown in Table 1, the first component (PC1) represents the main component that would distinguish between epithelial and mesenchymal cell states. Among the genes with the top highest PC1 loadings, mesenchymal markers such as fibronectin (FN1) and two types of collagen (COL1A1, COL13A1) are involved, and in addition, genes related to cell adhesion (NEGR1, TNC) and cell motility (ARHGAP24) are also included. They are typical marker genes that discriminate the epithelial and mesenchymal states.
The top 20 principal components loadings of the first and second components.
| (a) The top 20 PC1 loadings . | ||
|---|---|---|
| Gene symbol . | Gene name . | PC1 loading . |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.261823 |
| FN1 | Fibronectin | 0.238429 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.206869 |
| COL1A1 | Collagen, type I, alpha 1 | 0.203478 |
| NEGR1 | Neuronal growth regulator 1 | 0.190520 |
| FBN1 | Fibrillin 1 | 0.187782 |
| ARMCX1 | Armadillo repeat containing, X-linked 1 | 0.182721 |
| WNT5B | Wingless-type MMTV integration site family, member 5B | 0.182222 |
| XK | X-linked Kx blood group | 0.172636 |
| BAALC | Brain and acute leukemia, cytoplasmic | 0.163815 |
| GAP43 | Growth associated protein 43 | 0.157189 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.156683 |
| COL13A1 | Collagen, type XIII, alpha 1 | 0.156403 |
| DSC2 | Desmocollin 2 | 0.154287 |
| PLSCR4 | Scramblase 4 | 0.148105 |
| TNC | Tenascin C | 0.143167 |
| RCAN2 | Regulator of calcineurin 2 | 0.140531 |
| 1560208_at | 0.135836 | |
| ARHGAP24 | Rho GTPase activating protein 24 | 0.135123 |
| (b) The top 20 PC2 loadings | ||
| Gene symbol | Gene name | PC2 loading |
| DSC2 | Desmocollin 2 | 0.266742 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.264823 |
| ASPM | Asp (abnormal spindle) homolog, microcephaly associated | 0.258160 |
| HMMR | Hyaluronan-mediated motility receptor (RHAMM) | 0.246326 |
| PBK | PDZ binding kinase | 0.238582 |
| CKMT1A/1B | Creatine kinase, mitochondrial 1A/1B | 0.221564 |
| AP1S3 | Adaptor-related protein complex 1, sigma 3 subunit | 0.217856 |
| MIR222HG | mir host gene | 0.216734 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.192942 |
| MAD2L1 | MAD2 mitotic arrest deficient-like 1 | 0.189140 |
| CCNB1 | Cyclin B1 | 0.173976 |
| CLIP3 | CAP-GLY domain containing linker protein 3 | 0.171328 |
| KCND3 | Potassium channel, voltage gated Shal related subfamily D, member 3 | 0.169711 |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.159304 |
| HPS3 | Hermansky–Pudlak syndrome 3 | 0.144361 |
| GAP43 | Growth associated protein 43 | 0.133483 |
| PVRL3 | Poliovirus receptor-related 3 | 0.132407 |
| BRI3BP | BRI3 binding protein | 0.132175 |
| XK | X-linked Kx blood group | 0.128981 |
| (a) The top 20 PC1 loadings . | ||
|---|---|---|
| Gene symbol . | Gene name . | PC1 loading . |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.261823 |
| FN1 | Fibronectin | 0.238429 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.206869 |
| COL1A1 | Collagen, type I, alpha 1 | 0.203478 |
| NEGR1 | Neuronal growth regulator 1 | 0.190520 |
| FBN1 | Fibrillin 1 | 0.187782 |
| ARMCX1 | Armadillo repeat containing, X-linked 1 | 0.182721 |
| WNT5B | Wingless-type MMTV integration site family, member 5B | 0.182222 |
| XK | X-linked Kx blood group | 0.172636 |
| BAALC | Brain and acute leukemia, cytoplasmic | 0.163815 |
| GAP43 | Growth associated protein 43 | 0.157189 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.156683 |
| COL13A1 | Collagen, type XIII, alpha 1 | 0.156403 |
| DSC2 | Desmocollin 2 | 0.154287 |
| PLSCR4 | Scramblase 4 | 0.148105 |
| TNC | Tenascin C | 0.143167 |
| RCAN2 | Regulator of calcineurin 2 | 0.140531 |
| 1560208_at | 0.135836 | |
| ARHGAP24 | Rho GTPase activating protein 24 | 0.135123 |
| (b) The top 20 PC2 loadings | ||
| Gene symbol | Gene name | PC2 loading |
| DSC2 | Desmocollin 2 | 0.266742 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.264823 |
| ASPM | Asp (abnormal spindle) homolog, microcephaly associated | 0.258160 |
| HMMR | Hyaluronan-mediated motility receptor (RHAMM) | 0.246326 |
| PBK | PDZ binding kinase | 0.238582 |
| CKMT1A/1B | Creatine kinase, mitochondrial 1A/1B | 0.221564 |
| AP1S3 | Adaptor-related protein complex 1, sigma 3 subunit | 0.217856 |
| MIR222HG | mir host gene | 0.216734 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.192942 |
| MAD2L1 | MAD2 mitotic arrest deficient-like 1 | 0.189140 |
| CCNB1 | Cyclin B1 | 0.173976 |
| CLIP3 | CAP-GLY domain containing linker protein 3 | 0.171328 |
| KCND3 | Potassium channel, voltage gated Shal related subfamily D, member 3 | 0.169711 |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.159304 |
| HPS3 | Hermansky–Pudlak syndrome 3 | 0.144361 |
| GAP43 | Growth associated protein 43 | 0.133483 |
| PVRL3 | Poliovirus receptor-related 3 | 0.132407 |
| BRI3BP | BRI3 binding protein | 0.132175 |
| XK | X-linked Kx blood group | 0.128981 |
The top 20 principal components loadings of the first and second components.
| (a) The top 20 PC1 loadings . | ||
|---|---|---|
| Gene symbol . | Gene name . | PC1 loading . |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.261823 |
| FN1 | Fibronectin | 0.238429 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.206869 |
| COL1A1 | Collagen, type I, alpha 1 | 0.203478 |
| NEGR1 | Neuronal growth regulator 1 | 0.190520 |
| FBN1 | Fibrillin 1 | 0.187782 |
| ARMCX1 | Armadillo repeat containing, X-linked 1 | 0.182721 |
| WNT5B | Wingless-type MMTV integration site family, member 5B | 0.182222 |
| XK | X-linked Kx blood group | 0.172636 |
| BAALC | Brain and acute leukemia, cytoplasmic | 0.163815 |
| GAP43 | Growth associated protein 43 | 0.157189 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.156683 |
| COL13A1 | Collagen, type XIII, alpha 1 | 0.156403 |
| DSC2 | Desmocollin 2 | 0.154287 |
| PLSCR4 | Scramblase 4 | 0.148105 |
| TNC | Tenascin C | 0.143167 |
| RCAN2 | Regulator of calcineurin 2 | 0.140531 |
| 1560208_at | 0.135836 | |
| ARHGAP24 | Rho GTPase activating protein 24 | 0.135123 |
| (b) The top 20 PC2 loadings | ||
| Gene symbol | Gene name | PC2 loading |
| DSC2 | Desmocollin 2 | 0.266742 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.264823 |
| ASPM | Asp (abnormal spindle) homolog, microcephaly associated | 0.258160 |
| HMMR | Hyaluronan-mediated motility receptor (RHAMM) | 0.246326 |
| PBK | PDZ binding kinase | 0.238582 |
| CKMT1A/1B | Creatine kinase, mitochondrial 1A/1B | 0.221564 |
| AP1S3 | Adaptor-related protein complex 1, sigma 3 subunit | 0.217856 |
| MIR222HG | mir host gene | 0.216734 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.192942 |
| MAD2L1 | MAD2 mitotic arrest deficient-like 1 | 0.189140 |
| CCNB1 | Cyclin B1 | 0.173976 |
| CLIP3 | CAP-GLY domain containing linker protein 3 | 0.171328 |
| KCND3 | Potassium channel, voltage gated Shal related subfamily D, member 3 | 0.169711 |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.159304 |
| HPS3 | Hermansky–Pudlak syndrome 3 | 0.144361 |
| GAP43 | Growth associated protein 43 | 0.133483 |
| PVRL3 | Poliovirus receptor-related 3 | 0.132407 |
| BRI3BP | BRI3 binding protein | 0.132175 |
| XK | X-linked Kx blood group | 0.128981 |
| (a) The top 20 PC1 loadings . | ||
|---|---|---|
| Gene symbol . | Gene name . | PC1 loading . |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.261823 |
| FN1 | Fibronectin | 0.238429 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.206869 |
| COL1A1 | Collagen, type I, alpha 1 | 0.203478 |
| NEGR1 | Neuronal growth regulator 1 | 0.190520 |
| FBN1 | Fibrillin 1 | 0.187782 |
| ARMCX1 | Armadillo repeat containing, X-linked 1 | 0.182721 |
| WNT5B | Wingless-type MMTV integration site family, member 5B | 0.182222 |
| XK | X-linked Kx blood group | 0.172636 |
| BAALC | Brain and acute leukemia, cytoplasmic | 0.163815 |
| GAP43 | Growth associated protein 43 | 0.157189 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.156683 |
| COL13A1 | Collagen, type XIII, alpha 1 | 0.156403 |
| DSC2 | Desmocollin 2 | 0.154287 |
| PLSCR4 | Scramblase 4 | 0.148105 |
| TNC | Tenascin C | 0.143167 |
| RCAN2 | Regulator of calcineurin 2 | 0.140531 |
| 1560208_at | 0.135836 | |
| ARHGAP24 | Rho GTPase activating protein 24 | 0.135123 |
| (b) The top 20 PC2 loadings | ||
| Gene symbol | Gene name | PC2 loading |
| DSC2 | Desmocollin 2 | 0.266742 |
| ENPP1 | Ectonucleotide pyrophosphatase/phosphodiesterase 1 | 0.264823 |
| ASPM | Asp (abnormal spindle) homolog, microcephaly associated | 0.258160 |
| HMMR | Hyaluronan-mediated motility receptor (RHAMM) | 0.246326 |
| PBK | PDZ binding kinase | 0.238582 |
| CKMT1A/1B | Creatine kinase, mitochondrial 1A/1B | 0.221564 |
| AP1S3 | Adaptor-related protein complex 1, sigma 3 subunit | 0.217856 |
| MIR222HG | mir host gene | 0.216734 |
| CNN1 | Calponin 1, basic, smooth muscle | 0.192942 |
| MAD2L1 | MAD2 mitotic arrest deficient-like 1 | 0.189140 |
| CCNB1 | Cyclin B1 | 0.173976 |
| CLIP3 | CAP-GLY domain containing linker protein 3 | 0.171328 |
| KCND3 | Potassium channel, voltage gated Shal related subfamily D, member 3 | 0.169711 |
| ELTD1 | EGF, latrophilin and seven transmembrane domain containing 1 | 0.159304 |
| HPS3 | Hermansky–Pudlak syndrome 3 | 0.144361 |
| GAP43 | Growth associated protein 43 | 0.133483 |
| PVRL3 | Poliovirus receptor-related 3 | 0.132407 |
| BRI3BP | BRI3 binding protein | 0.132175 |
| XK | X-linked Kx blood group | 0.128981 |
The second principal component (PC2) is thought to be related to cancer metastasis, because in the top 20 PC2 loadings, genes that are highly expressed in the cancer metastatic stage are involved, such as HMMR, PBK, CKMT1A/1B, and BRI3BP. Furthermore, several genes have high PC2 loadings, which are deeply related to the cell cycle (especially the mitotic phase) such as cyclin B1 and MAD2L1, the aberrations of which are found in various cancers.
The statistical and quasi-potential distribution of epithelial and mesenchymal cell states
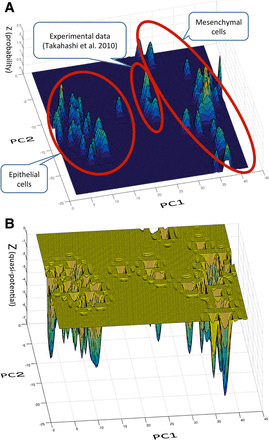
The statistical distribution of GRN states in the vicinity of the epithelial and mesenchymal cell states in the GRN subspace is shown in Figure 1 A. As we can see in Figure 1A, the obtained statistical distribution is multi-modal, showing several peaks in both the major epithelial and mesenchymal cell groups (encircled respectively in Figure 1A). This is because, even if a cell belongs to the epithelial or mesenchymal cell type, there are various subtypes within that cell type, respectively. But the peaks of the same cell types are located almost together in the same respective vicinity to make major groups, respectively. In Figure 1A, the peaks located on the left-hand side belong to major epithelial cell group and peaks located on the right-hand side belong to the major mesenchymal cell group. The epithelial and mesenchymal cell groups are separate along with the axis of PC1.
Statistical and quasi-potential distribution of epithelial and mesenchymal states. (A) Statistical distribution of epithelial and mesenchymal states. We created a statistical distribution of cell states of epithelial and mesenchymal cells in the state space of the gene network. To do this, we empirically collected samples of gene expression profiles from GEO and ArrayExpress (Supplementary Table S1). We chose coordinate variables (genes) by extracting genes whose expression profiles differed significantly between the epithelial and mesenchymal cell states. To depict a three-dimensional view of the statistical distribution, we further applied principal component analysis to the above selected coordinate variables. We depicted a statistical distribution with the first and second component (PC1-PC2) as the x-y axis. In A, the peaks located on the left-hand side belong to the major epithelial cell groups and peaks located on the right-hand side belong to the major mesenchymal cell groups (encircled, respectively). On the contrary, the peaks of Takahashi et al.'s time-course gene expression profiles for experimental EMT were located along the axis of the second component (PC2), whereas the major groups of epithelial and mesenchymal cell states are aligned mostly along the PC1 axis. (B) Quasi-potential distribution in the state space of the gene network. By application of Boltzmann's formula (ψ = −k log φ) to the empirical statistical distribution in A, we obtained a quasi-potential distribution which is considered the same as Waddington's epigenetic landscape. Basins located on the left-hand side area belong to the epithelial states group, and basins on the right-hand side area belong to the mesenchymal state group. The basin in the middle space comprises the time-course potentials by Takahashi et al.'s experimental data (Takahashi et al., 2010).
In contrast, the epithelial and mesenchymal states in the time-course gene expression profiles for experimental EMT, reported by Takahashi et al., were found to be located separately both from the major epithelial and mesenchymal cell groups: they were located in the middle between those two groups and along the axis of the second component (PC2), which is different from and almost vertical to the direction in which major groups of epithelial and mesenchymal cell states are aligned, mostly along with PC1 axis.
This is because, as we have previously described in the interpretation of the principal components, PC1 is the component that generally distinguishes between epithelial and mesenchymal cell states, whereas PC2 represents a component more specific to the cancer metastatic changes of the cell state. The peaks of statistical distribution of Takahashi et al.'s data in this GRN subspace are the initial (epithelial) and terminal (mesenchymal) states of the EMT process during cancer metastasis, which would progress along the PC2 axis.
The quasi-potential distribution, which was obtained by application of Boltzmann's formula (ψ = −k log φ) to the statistical distribution is shown in Figure 1B, also in a wider view.
The EMT trajectory in the GRN-space landscape
Two-dimensional depiction of the trajectory of EMT and cluster analysis
The state loci on the GRN space during the process of EMT were depicted by again using the time-course gene expression data of Takahashi et al. In Takahashi et al.'s experiment, gene expression profiles were measured at six time points (0, 1, 6, 16, 24, 42, and 60 h) after the onset of EMT, where observations at each time point were repeated three times, except for those at 1 h after the onset of EMT, which were repeated twice.
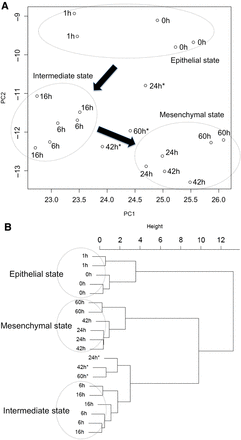
The EMT states corresponding to all the measured gene expression profiles by Takahashi et al.'s experiment were projected onto the z = 0 plane of PC1-PC2 coordinates, as shown in Figure 2A. We applied the Ward's hierarchical clustering method to the totally 17 EMT states. The result in the form of dendrogram is shown in Figure 2B. The classification by the dendrogram clearly shows the three state groups, which could be called epithelial, mesenchyma and intermediate states, with several outliers (denoted by an asterisk). The resultant grouping of the states is also depicted in Figure 2A with dotted circles. From Figure 2A, in the cancer EMT process, epithelial states do not directly transit to mesenchymal states but first transit along a considerably different direction to intermediate states and then, turning direction, transit to mesenchymal states. This suggests that the course of EMT occurs in three stages and that the intermediate stage has a certain degree of individuality.
The loci of cancer EMT obtained by using Takahashi et al.'s time-course gene expression data (Takahashi et al., 2010) in the PC1-PC2 coordinates and a dendrogram of Ward's hierarchical clustering of those states. (A) The loci of cancer EMT obtained by using Takahashi et al.'s time-course gene expression data in PC1-PC2 coordinates during the cancer EMT. The loci of the states are depicted in (PC1-PC2) coordinates. The results of Ward's hierarchical cluster analysis are indicated by encircled points with three outliers (noted by asterisks). (B) The dendrogram of results classified by Ward's hierarchical cluster analysis: three states groups (epithelial, intermediate, and mesenchymal states) and outliers (noted by asterisks).
The trajectory of the EMT in GRN-space landscape
We depicted the EMT trajectory indicated by Takahashi et al.'s data in three-dimensional GRN-space landscape by the following procedures: The sequence of the state points on the quasi-potential surface during the EMT process forms the trajectory of cancer EMT.
All the gene expression profiles at each time point were averaged to obtain the ‘centroid state’ for each time in the PC1-PC2 coordinates,
The quasi-potential values (z-axis depths) of the centroid states were calculated and mapped onto the quasi-potential distribution surface.
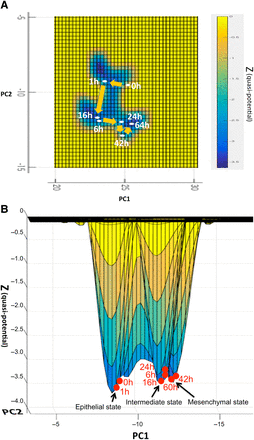
The overhead view of the trajectory of the centroid states in the GRN-space landscape was depicted on the PC1-PC2 plane (z = 0) in Figure 3A, showing the depth of quasi-potential values of the centroid states by the varying shades. From Figure 3A, we could clearly discern three basins formed along with the trajectory of cancer EMT. A lateral view of the EMT centroid states at six time points on the quasi-potential surface is shown in Figure 3B. The trajectory can be estimated from these loci of the EMT states: starting from the epithelial basin of the RPE cell, staying in an intermediate basin, then climbing over the epigenetic barrier (separating ridge), and finally falling down to settle on the bottom of the mesenchymal basin of the RPE cell. There are three basins on the trajectory of cancer EMT.
Trajectory of the averaged (centroids) states during the cancer EMT process. (A) Overhead view of the EMT process on quasi-potential distribution (quantified Waddington's epigenetic landscape). Trajectory of the averaged (centroid) states at six time points (0, 1, 6, 16, 24, 42, and 64 h) of the EMT process are plotted on the (PC1-PC2) plane (z = 0). This is an overhead view of the trajectory of EMT states on the quasi-potential distribution (quantified Waddington's epigenetic landscape) in the state space. The degree of depth of the quasi-potential distribution is indicated by the varying shades. We can see that there are three basins on the trajectory of the EMT process. (B) Lateral view of EMT process on quasi-potential distribution (quantified Waddington's epigenetic landscape). Trajectory of the averaged (centroid) states of the EMT process at each time point (0, 1, 6, 16, 24, 42, and 64 h) is depicted on the quasi-potential surface (quantified Waddington's epigenetic landscape). We can easily see that three basins along the EMT process.
Estimation of overall structural change of the gene network during EMT
To confirm whether this three stage transition takes place in the activation pattern of a gene network during the cancer EMT process, we estimated overall structural changes of a gene network by using the time-course gene expression profile data of Takahashi et al. (2010) again.
Selection of genes to infer activation pattern of the gene network during EMT
In estimating structural changes of the gene network during cancer EMT, we first selected genes that are expected to comprise building components (genes) of an estimated gene network. We selected the following genes, which are thought to contribute significantly to the structural changes of the gene network caused by cancer EMT.
Genes that showed large variations between time points during EMT
We first selected genes with expression levels that vary significantly between sequential time points. As a result, 3421 probe sets were selected in the microarray, which corresponds to 1766 genes.
Genes monotonously increasing and decreasing during EMT
Secondly, we selected genes with expression levels that increased or decreased monotonously throughout the time-course of cancer EMT. We used accumulated chi-squared test (Hirotsu, 1986) to detect those genes. In this way, we selected 1689 probe sets, which is equal to 1203 genes.
Known epithelial/mesenchymal marker genes and EMT related genes.
Finally, we also selected 34 genes frequently cited as marker genes of epithelial or mesenchymal cells and also as EMT-related genes in the literature. Totally, by eliminating the overlapping genes, we selected 5183 probe sets, equal to 2988 genes, to infer the gene network of cancer EMT.
Inference of the gene network of cancer EMT by ARACNe
We used gene expression profile data of Takahashi et al. (2010) to estimate the gene network by ARACNe algorithm. We used only the gene expression profile data of the above selected genes. The ARACNe algorithm is a method that infers a gene network from the gene expression profile observed by microarray.
In estimating the gene network of cancer EMT by ARACNe, we used all of the time-course data at six time points of the gene expression profiles for the 2988 selected genes. One reason for doing this is because we had only two or three samples in each time point. Thus, we could not infer the gene network at each time point with sufficient reliability. Another reason is that we reasonably assumed that the mode of interaction (regulation) between genes is essentially the same throughout the course of EMT, although the interaction between genes becomes active in some stages but silent in others. Hence, we adopted the following strategy to deal with a network temporally changing in its activation structure. We first used all of the temporal data to estimate an ‘intrinsically’ connected structure of the gene network during the EMT process, and then divided the total time span into several segments, and for each, the active part of the connections in the whole gene network is depicted. The estimated intrinsic gene network is shown in Figure 4 with 2988 nodes (genes) and 17368 connections (regulations) of the network.
Inferred gene regulatory network of cancer EMT. We used time-course gene expression data (Takahashi et al., 2010) of cancer EMT of selected genes (2988 genes) to infer the gene regulatory network (17368 regulations) by the ARACNe algorithm (P < 1.0 × 10−10; bootstrap >90%).
Master regulator analysis applied to estimated gene network
The estimated gene network was too complex to understand the main structural changes. We conducted the master regulator analysis on the above gene network of cancer EMT inferred by ARACNe. In the master regulator analysis, most of the transcription factors (TFs) in major TF databases (about 1800 TFs) were investigated to see whether they regulate a significantly greater number of differentially expressed genes in the network inferred by ARACNe, than expected. We used Fisher exact test for this purpose with significance level, P < 0.05. We obtained the 11 master regulators listed in Table 2.
List of the selected master regulators.
| Transcription factors . | N of DEG (SAM; P < 0.0001, FC > 1.5) . | P-value (Fisher exact test) . |
|---|---|---|
| TCF3 | 86/135 | 2.20 × 10−16 |
| ZEB1 | 46/592 | 8.58 × 10−16 |
| SMAD2 | 36/317 | 0.000209 |
| TWIST1 | 16/154 | 0.005634 |
| TP63 | 6/7 | 0.01302 |
| FOSL2 | 5/6 | 0.02516 |
| PPARA | 5/7 | 0.03732 |
| ARNTL2 | 15/38 | 0.03843 |
| MXD1 | 4/5 | 0.04918 |
| MITF | 4/5 | 0.04918 |
| NR2F2 | 4/5 | 0.04918 |
| Transcription factors . | N of DEG (SAM; P < 0.0001, FC > 1.5) . | P-value (Fisher exact test) . |
|---|---|---|
| TCF3 | 86/135 | 2.20 × 10−16 |
| ZEB1 | 46/592 | 8.58 × 10−16 |
| SMAD2 | 36/317 | 0.000209 |
| TWIST1 | 16/154 | 0.005634 |
| TP63 | 6/7 | 0.01302 |
| FOSL2 | 5/6 | 0.02516 |
| PPARA | 5/7 | 0.03732 |
| ARNTL2 | 15/38 | 0.03843 |
| MXD1 | 4/5 | 0.04918 |
| MITF | 4/5 | 0.04918 |
| NR2F2 | 4/5 | 0.04918 |
In the middle column, ratio shows the number of the significantly differential genes, which are controlled by the master regulator, divided by the number of genes it controls. If the ratio is significantly high, then the transcription factor is acknowledged as a master regulator. N: number, DEG: differentially expressed gene.
List of the selected master regulators.
| Transcription factors . | N of DEG (SAM; P < 0.0001, FC > 1.5) . | P-value (Fisher exact test) . |
|---|---|---|
| TCF3 | 86/135 | 2.20 × 10−16 |
| ZEB1 | 46/592 | 8.58 × 10−16 |
| SMAD2 | 36/317 | 0.000209 |
| TWIST1 | 16/154 | 0.005634 |
| TP63 | 6/7 | 0.01302 |
| FOSL2 | 5/6 | 0.02516 |
| PPARA | 5/7 | 0.03732 |
| ARNTL2 | 15/38 | 0.03843 |
| MXD1 | 4/5 | 0.04918 |
| MITF | 4/5 | 0.04918 |
| NR2F2 | 4/5 | 0.04918 |
| Transcription factors . | N of DEG (SAM; P < 0.0001, FC > 1.5) . | P-value (Fisher exact test) . |
|---|---|---|
| TCF3 | 86/135 | 2.20 × 10−16 |
| ZEB1 | 46/592 | 8.58 × 10−16 |
| SMAD2 | 36/317 | 0.000209 |
| TWIST1 | 16/154 | 0.005634 |
| TP63 | 6/7 | 0.01302 |
| FOSL2 | 5/6 | 0.02516 |
| PPARA | 5/7 | 0.03732 |
| ARNTL2 | 15/38 | 0.03843 |
| MXD1 | 4/5 | 0.04918 |
| MITF | 4/5 | 0.04918 |
| NR2F2 | 4/5 | 0.04918 |
In the middle column, ratio shows the number of the significantly differential genes, which are controlled by the master regulator, divided by the number of genes it controls. If the ratio is significantly high, then the transcription factor is acknowledged as a master regulator. N: number, DEG: differentially expressed gene.
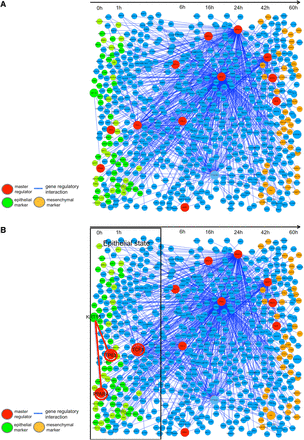
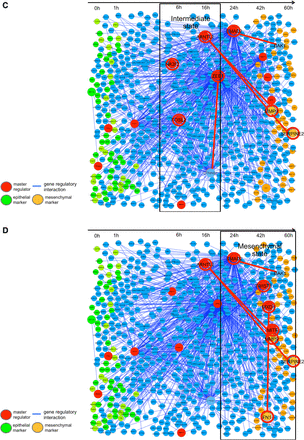
We inferred the intrinsic gene network, as the first step, throughout the whole time-course of cancer EMT in Figure 5A. This gene network comprises the genes that are directly regulated by the 11 selected master regulators (major transcription factors). For this depiction, we arranged genes (nodes) along with the time axis in such an order that each of the genes reaches its peak expression levels along the time axis.
Master regulators and their regulation activity in the cancer EMT gene network. Inference of the gene network EMT directly regulated by 11 master regulators was obtained. (A) The Intrinsic network of EMT inferred by ARACNe is shown in the whole time axis. The master regulators that significantly regulate the differentially expressed genes with a significance level, P < 0.05, and the gene network regulated by them are depicted. (B) The first stage (epithelial state stage). KRT18 and TP63 are expressed in the epithelial stage. A master regulator, TP63, was estimated to regulate KRT18. (C) The middle stage (intermediate transient stage). A transcription factor, CTNNB1, is shown inducing the expression of ZEB1. The CTNNB1 is known to be a key factor inducing the EMT process. ZEB1 is also a master regulator and was known to down-regulate epithelial marker genes like CDH1. (D) The final stage (mesenchymal state stage). SMAD2 is a master regulator, and induced such mesenchymal marker genes as MMP9, and FN1, and SERPINE2. TWIST1 is also a master regulator, and in fact, has been reported to be essential for induction of the EMT process.
Three staged process of cancer EMT
Corresponding to the three stage structure found by analysis of the EMT state trajectory, we divided the entire time-course changes of the gene network into three temporal spans corresponding to the above three stages, within each of which the cellular state stayed in separate potential basins in the GRN-space landscape.
In the first stage of the cancer EMT process, which lasts from 0 to 1 h, the representative master regulators are tumor protein p63 (TP63) and transcription factor 3 (TCF3). TCF3 is a well-known EMT inducer, and TP63 plays an important role in the development and maintenance of stratified epithelial tissues (Tucci et al., 2012), thus regulating the expression of keratin, type I cytoskeletal 18 (KRT18). In this stage, global features of the cell state still exhibit epithelial characteristics. KRT18 and TP63 are both key marker genes for epithelial cells.
During this stage, the cell states remain in the potential basin for the epithelial stage. Because of a shortage of strong mutual information, the well-known epithelial marker gene CDH1 (e-cadherin) was dropped from this master regulator network, but KRT18 and TP63 remain in the network of this stage as epithelial marker genes (Figure 5B). The role of TCF3 is in long-term maintenance and wound repair of epidermis (Nguyen et al., 2009). Thus these two master regulators TP63 and TCF3, as estimated by master regulator analysis in this stage, are concerned with epithelium maintenance and this stage remains in the basin of epithelial cell types.
In the second stage of cancer EMT, CTNNB1 (catenin β1), which is connected with and controls the epithelial marker CDH1, was inferred to induce the expression of ZEB1 (zinc finger E-box binding homeobox 1). This regulatory link showed that the EMT process is triggered by CTNNB1, which is part of a protein complex that constitutes the adherents junctions necessary for the creation and maintenance of epithelial cell layers, by regulating cell growth and adhesion between cells. CTNNB1 in complex with TCF4 induces EMT-activator ZEB1 to regulate tumor invasiveness (Sánchez-Tilló et al., 2011). ZEB1 induces epithelial cells to abandon their tight adhesion and assume a more mobile and loosely associated mesenchymal phenotype by suppressing CDH1 and promoting the expression of vimentin, fibronectin and collagen type 1. ZEB1 is known as the most influential activator of EMT, by down-regulating epithelial maker genes and promoting the mesenchymal marker genes. ZEB1 maintains the stemness by repressing expression of stemness-inhibiting miRNAs (Wellner et al., 2009). We denoted this stage as an intermediate transient stage that is the main driving stage for the cancer EMT process (Figure 5C). In this stage, the estimated master regulators were ZEB1 and aryl hydrocarbon receptor nuclear translocator-like 2 (ARNTL2). ARNTL2 is the master regulator of the mesenchymal marker genes of matrix metallopeptidase 9 (MMP9) and serpin peptidase inhibitor, clade E genes, member 2 (SERPINE2). In this stage, ARNTL2 becomes active to bring about the activity of mesenchymal marker genes (Mazzoccoli et al., 2011). We can consider this stage as the most important intermediate stage to drive EMT.
The stage beginning at 24 h after the start of the EMT process is a critical time point staying at the ridge between the second stage basin and the final stage mesenchymal basin, which might belong to either the second intermediate or the third stage. In this study, we classified this state at 24 h after the onset of EMT as belonging to the third stage.
In the third stage, SMAD family member 2 (SMAD2) becomes a master regulator, and was inferred to induce such mesenchymal marker genes as MMP9, fibronectin 1 (FN1), and SERPINE2 (Islam et al., 2014). SMAD2 is triggered by the TGF-β signaling pathway and contributes to maintaining the mesenchymal phenotype. SMAD2 modulates the extracellular matrix for the mesenchymal state to prepare the final stage of cancer EMT. Twist-related protein 1 (TWIST1) was also an estimated master regulator, and in fact, was reported to be essential for repressing epithelial marker genes and inducing the mesenchymal state (Galván et al., 2015) (Figure 5D).
Structural changes in the gene network were observed with respective groups of major master regulators alternatively taking important roles along the time-course to regulate the different activation patterns of the gene network Figure 5B–D.
Discussion
A new empirical method to create a quantitative Waddington's epigenetic landscape
In this study, it was considered that Waddington's landscape is the same as a quasi-potential distribution defined on all the cell states, where the elevation of the potential surface is inversely related to the likelihood that the corresponding cell state will occur. As mentioned before, the studies by Huang and Wang have been conducted to create Waddington's epigenetic landscape mathematically. In this study, we proposed a new method for creating Waddington's epigenetic landscape.
The first feature of our method is to create a quasi-potential distribution empirically, by collecting samples of gene expression profiles from repository databases such as GEO or ArrayExpress. The gene expression profiles are determined by activation patterns of gene networks, so that we consider the state of a gene network and a gene expression profile as being essentially the same and use these concepts interchangeably.
The mathematical approach to construct a quantitative Waddington's epigenetic landscape as described in Huang's and Wang's studies has a limitation in that they deal with a very simple landscape created by two or three variables (genes), such as a landscape of a mutually suppressing loop of two genes (Huang et al., 2009; Wang et al., 2014). Although these mathematical methods could clarify theoretical characteristics of the Waddington's landscape, those would not be useful to help solve real problems, for example, to utilize the trajectory of cancer EMT to clarify the mechanism of cancer metastasis or to explore the best reprogramming pathway in regenerative medicine.
As for the individual quasi-potential distribution of each cell type , its calculation from datasets of gene expression profiles of cell type i, would become more unbiased (accurate) toward a true distribution as the number of sample profiles increases. Such a trend might well be expected, as seen from the current speed of sample accumulation in the databases.
On the other hand, it is not so straightforward to determine exact values of pi. The prior probability pi affects the depth of a potential basin of cell type i in the landscape. The sample number of gene expressions of different cell types in the various databases may be biased due to the aforementioned reasons. For this problem, when the tissue or organ in which we create the quasi-potential distribution is well defined, a possible solution is to estimate the ratios among the numbers of cell types contained in that tissue or organ. A rough estimate would be obtained from anatomical studies of that tissue or organ, or from repository databases containing a vast number of cell types, such as CELPEDIA (Hatano et al., 2011). A more rigorous solution is to directly measure the ratio among the numbers of cell types in the tissue or organ by utilizing automatic cell counters which are now available (Grishagin, 2015). In our study, the main concern is the configuration of potential basins. Furthermore, the data we use for the analysis of cancer EMT is confined to the single experiment by Takahashi et al. Hence, in this study there is not a serious problem of unbiased sampling.
Coordinate system of GRN space and principal components
The next feature of our empirical method for Waddington's landscape is our way of constructing a coordinate system in which statistical and quasi-potential distributions are created. Gene expression profiles are multi-dimensional data with dimensions equal to the total number of genes or probes on microarray. To explore the best coordinate system suitable for the given problem with the reduced number of variables (genes) is a crucial issue. In this study, the EMT process is the main subject; thus, we selected a set of coordinate variables (genes), whose expression profiles differ significantly between the epithelial and mesenchymal cell states.
We then applied a principal component analysis to expression data of the above selected genes. By using the obtained first and second components as x-y coordinates, we depicted the statistical and quasi-potential distribution for GRN states along the direction of the z axis. We estimated the meaning of the first and second principal components by investigating genes with the top 20 highest PC loadings. As already mentioned in ‘Results’, we consider that the first principal component (PC1) means the general features distinguishing the epithelial and mesenchymal cell states, whereas the second principal component (PC2) represents the state change in the cancer metastasis. From the statistical distribution of various epithelial and mesenchymal states collected from the gene expression databases, at least these two principal components (PC1 and PC2) are necessary to locate the various types of epithelial and mesenchymal states separately. As mentioned before, major epithelial and mesenchymal cell groups are aligned along the PC1 axis and the cancer EMT process by Takahashi et al.'s experiment is along the PC2 axis. We should take note that collected epithelial and mesenchymal cell data contain not only those from cancer cell lines but also those from the reprogramming experiment where fibroblasts are transited to iPS cells for example (GSE9832 in Supplementary Table S1). Hence, to locate the various epithelial and mesenchymal states separately in the GRN space, two principal components are found to be at least necessary.
The quantified Waddington epigenetic landscape
In the quasi-potential field (GRN-space landscape), each stable cell state forms a potential basin, the bottom of which is the most stable and commonly observed state. By depicting the EMT process of Takahashi et al.'s data, we demonstrated that cancer EMT is movement departing from an epithelial basin, staying in an intermediate basin, climbing over an epigenetic barrier, and finally falling down to a mesenchymal basin; thus, transitioning through three sequential stages.
The equivalence between the GRN space landscape and quantified Waddington's epigenetic landscape is straightforward when dealing with a subspace of terminally differentiated adult cell types. All the terminally differentiated adult cell types, as would appear at the end-stage of development, can be equally dealt with in the GRN state space. Other cell types, however, which appear in early or middle stages of development, such as ES/iPS cells or various stem/progenitor cells, are not dealt with the same as terminally differentiated cells in the GRN space created by our method.
There must be another axis or specified potential parameter that locates ES/iPS cells or stem/progenitor cells upstream from the terminally differentiated cell types in Waddington's epigenetic landscape. Presently, we cannot find the appropriate axis or parameter that represents the sequential order in development to produce the overall inclined surface of Waddington's epigenetic landscape. Consequently, in this study we depict Waddington's landscape only within the restricted subspace of terminally differentiated adult cells. Although our quantified Waddington's landscape depicts only the ‘flat’ space comprising the terminally differentiated adult cell types at the foot of the landscape, it might be useful for depicting the cancer EMT process as described in this study or the direct reprogramming between the cell types in regenerative medicine that, without returning to upstream ES/iPS cell states, moves transversally from one matured cell type to another.
Trajectory of the EMT process and three stages of cancer EMT
We depicted temporal locations of averaged (centroids) states of the cancer EMT process of Takahashi et al.'s data in the GRN-space landscape. Although the number of experimental samples was small, we succeeded in depicting the quasi-potential distribution trajectory along the process of cancer EMT, upon which we traced the average gene expression profiles (centroid states) of each time point for 0, 1, 6, 16, 24, 42, and 64 h after the start of EMT.
At 0 and 1 h after the onset of EMT, the gene network still remains in an epithelial basin, showing that the location for this state of the gene network is in the first basin. At 6 and 16 h after the onset of EMT, the gene network is transitioned into the second intermediate basin which we will discuss in detail below. After leaving the intermediate stage, the trajectory proceeds to climb up the epigenetic barrier to overcome the adjoining epigenetic barrier (24 h) to reach the final basin of the mesenchymal state.
From this trajectory on the GRN-space landscape, we found that during the process of cancer EMT, three groups of states form the separate basins. The first basin is epithelial and the final basin is mesenchymal, but the intermediate basin is near both basins and, even though in the process of moving to the mesenchymal state, it is a relatively stable state to form a potential basin. The intermediate basin is on the epigenetic barrier located within the course from the epithelial to the mesenchymal states, but the trajectory stays with relative time so that a stable basin is formed around that state.
As for the meaning of the second stage of cancer EMT process, we would refer to the dynamical network theory of complex disease proposed by Chen et al. (2012) and Liu et al. (2014). From the theoretical analysis of nonlinear dynamical systems, Chen divided the disease progression process into three stages: a normal state, a pre-disease state (or a critical state), and a disease state. He especially characterized the second stage as a critical transition state, in that, when the system reached the critical transition state, a strongly and dynamically correlated gene subnetwork (‘dominant group of molecules’) (Chen et al., 2012) emerges and brings the system to the state of critical transition, where the expression level of the members of this subnetwork increasingly fluctuates in a cooperative way. Based on these features, Chen introduced the dynamical network biomarker (DNB) and found many DNSs from various complex diseases.
Following Chen's concept, the second stage of EMT could be considered as a critical transition stage from the epithelial to the mesenchymal state. Since the number of samples at each time point of Takahashi et al.'s data is so scarce, we cannot reach a definite conclusion. It is suggested, however, that at least two of the master regulators (ZEB1, TCF3) and a key molecule CTNNB1 might satisfy the necessary conditions that would allow the critical transition to take place. That is, in the second stage, the correlation coefficients among these three genes are increasing as their variances become larger (Supplementary Figure S1). Thus, we might consider the second stage to be Chen's critical transition state, and several key molecules, such as ZEB1, TCF3, and CTNN1, are suggested to be involved in the ‘dominant group of molecules’ that brings the cell state to the critical transition in cancer EMT.
Biological meanings of three stages and interrelation among the major master regulators
In this study, the essential features of cancer EMT were investigated from the network biology view point. We consider that cancer EMT is not just an incidental aberration of the cellular process but a biologically deep structural change of the gene network, which would compare to ‘phase transition’ in physics. From this perspective, we created a quantified Waddington epigenetic landscape that is a quasi-potential representation of the likelihood of all the possible activation patterns of a gene network. Within this framework, we have succeeded in depicting the trajectory of the time-course gene expression profiles of the cancer EMT process onto the quasi-potential distribution in this landscape. By means of this representation, we can understand the essential features of the cancer EMT process from a broader and more dynamical point of view.
Another important result is the estimation of structural changes in a gene network during the cancer EMT. The master regulator analysis applied to the gene network inferred by ARACNe revealed various findings which are summarized as follows: We will consider the biological meaning of these findings. First, it is suggested that cancer EMT would be driven by a hand-over process of major master regulators: from the epithelial state to intermediate state, the activity of TCF3 as a major master regulator is handed over to ZEB1 in cooperation with CTNNB1 to bring about the critical transition state, and from the intermediate state to mesenchymal state, the role of major master regulator ZEB1 is handed over to SMAD2 which brings the cell state to a stable mesenchymal one. An activation sequence of the master regulators TCF3–ZEB1–SMAD2 drives the progression of cancer EMT. Among these major master regulators, ZEB1 is considered to be the most important regulator that suppresses the epithelial differentiation, maintains the stemness, and promotes the mesenchymal state.
Cancer EMT is three-staged process comprising epithelial, intermediate, and mesenchymal states, all of which are relatively stable states forming respective potential basins.
From the structural changes occurring in the gene network during cancer EMT, major master regulators alternatively take a main role along the subsequent three stages to regulate the stage-specific activation patterns of the gene network. From our master regulator analysis, the major master regulators in each stage are, TCF3 and TP63 in the epithelial state, ZEB1 with relation to CTNNB1 in the intermediate state, and SMAD2 and TWIST in the mesenchymal state.
The intermediate state of the cancer EMT is considered to correspond to the specific features of Chen's critical transition state, whereby several key molecules such as TCF3, CTNNB1, and ZEB1 are highly correlated with increasing variances in the intermediate state.
CTNNB1 is not a transcription factor, but, together with TCF3, exhibits transcriptional activity for various genes. Furthermore, CTNNB1 plays a central role in various signaling pathways. Especially this molecule exhibits an important role in cooperation with TCF3 and ZEB1, one of which is to promote the critical transition.
The expression levels of master regulators that suppress the epithelial activity or promote the mesenchymal activity such as TP63, PPARA, and TWIST are expressed only in a stage-specific way, whereas expression levels of the major master regulators, such as TCF3, ZEB1, SMAD2, and key molecule CTNNB1, are constantly high throughout the three stages, but the degree of their fluctuations and the mutual correlation patterns among them vary with time.
Carro et al. (2010) applied master regulator analysis to the GRN in malignant glioma which is inferred by ARACNe, and concluded that a small regulatory module containing C/EBPβ and STAT3 initiates and controls the mesenchymal transformation. Similarly to Caro's conclusion, we might consider that the subnetwork involving TCF3, ZEB1, CTNNB1, and SMAD acts as a central regulator network to govern the whole process of EMT, whereby stage-specific activation of this central regulator subnetwork causes the three stages of EMT, and especially TCF3, ZEB1, and CTNNB1 become tightly correlated to cause the intermediate stage (critical transition).
Materials and methods
Construction of the GRN-space landscape and the EMT trajectory
Collection of gene expression profiles and construction of the GRN-space with statistical and quasi-potential distribution
We collected gene expression profiles both of epithelial cell types and mesenchymal cell types from the GEO and ArrayExpress. Actually, we collected 13 datasets (71 data samples) from the GEO and 1 dataset from ArrayExpress (3 data samples) (Supplementary Table S1). All the profiles are measured by GeneChip (Affymetrix HGU133 Plus 2.0).
As for epithelial cells, we retrieved gene expression data of epithelial cells from the above datasets, but we restricted datasets to those of cell lines because gene expression profiles from clinical samples may have some interference. Hence, our collected samples included a human lung adenocarcinoma epithelial cell line from the NCI60 panel, a human breast cancer cell line, and a human stomach gastric adenocarcinoma cell line. As for mesenchymal cells, we retrieved gene expression data of mesenchymal cells. Also only the gene expression data of cell lines were included. Gene expression data such as fibroblast cells and fibroblast-like cells were collected. Some are from the reprogramming experiment where fibroblasts are transited to iPS cells (GSE9832 in Supplementary Table S1).
In addition to the above dataset, time-course gene expression profiles during the EMT process, which were observed by Takahashi et al. (GSE12548 of GEO), were included in this stage of the study depicting a GRN-space landscape for EMT. These experimental EMT data were obtained from a human retinal pigment epithelium (RPE) cell line (ARPE-19) in response to combination treatment with TGF-β and TNF-α, which induces cancer EMT. In Takahashi et al.'s experiment, total RNA was extracted and gene expression profiles were measured at six time points (0, 1, 6, 16, 24, 42, and 60 h) from the start of the treatment with TGF-β and TNF-α, by GeneChip (Affymetrix HGU133 Plus 2.0). Observations at each time point were repeated three times, with the exception of those at 1 h, which were repeated two times. Gene expression data were normalized and analyzed by the robust multi-array average (RMA) (Irizarry et al., 2003).
We used Takahashi et al.'s data at the start (0 h) for epithelial states and those at 60 h after the start for mesenchymal states for creation of the statistical distribution of epithelial and mesenchymal cell states.
In depicting the GRN-space landscape in the vicinity of epithelial and mesenchymal cell types, a full dimension GRN space was projected onto a subspace where the trajectory of cancer EMT could be sufficiently and clearly depicted. We chose a set of coordinate variables (genes) for this subspace, whose expression profiles differ significantly between the epithelial and mesenchymal cells. We used SAM (Significant Analysis of Microarray) (Tusher et al., 2001) to select the differentially expressed genes between the epithelial and mesenchymal cell groups with a significance level, P < 0.001. Thus, the selected 61 genes were used as coordinate variables for the GRN subspace depicting the EMT trajectory (see Supplementary Table S1 for gene name, gene ID, medians of gene expression and description by NCBI GENE).
To depict the GRN-space landscape in three dimensions, we applied the principal component analysis (pca) in R by using Bioconductor and its associated packages. The first and second components were used as x-y axes, and the statistical distribution is drawn onto this two-dimensional plane along the direction of the z axis. Then, a quasi-potential field was obtained by applying a negative logarithm transformation to the statistical distribution, as described above.
Time-course gene expression data of cancer EMT and drawing the EMT trajectory onto the GRN-space landscape
The EMT trajectory on the GRN-space landscape was depicted by again using the time-course gene expression data given in Takahashi et al.'s experiment.
The EMT trajectory obtained was depicted as follows: We depicted an overhead view and a lateral view of the trajectory of EMT states on a surface of quasi-potential distribution; a quantified Waddington epigenetic landscape.
All the gene expression profiles (two or three samples) at each time point were averaged to obtain the ‘centroid state’ for each time in the PC1-PC2 coordinates,
The quasi-potential values (z-axis quasi-potential depths) of the centroid states described with PC1 and PC2 coordinates were calculated and mapped onto the quasi-potential distribution surface.
Inference of in-large structural change of gene network during EMT
To confirm what is occurring in the gene network during the cancer EMT process, we inferred in-large structural changes of the gene network by again using Takahashi et al.'s time-course gene expression profile data.
Selection of genes used for inference of the gene network of cancer EMT
We selected the following genes which are thought to be contributing significantly to the structural changes of the gene network caused by cancer EMT.
Genes that show a large variation between the time points during EMT
We first selected genes with expression levels that varied significantly between the sequential time points. We utilized SAM to extract differentially expressed genes between the sequential time points with the significance level P < 0.001 and fold change >1.5 (or <0.75).
Genes monotonously increasing and decreasing during EMT
Secondly, we selected genes whose expression level had been increasing or decreasing monotonously throughout the time-course of the cancer EMT. We used the accumulated chi-squared test to detect those genes.
Known epithelial/mesenchymal marker genes and EMT related genes.
We included 34 marker genes of epithelial or mesenchymal cells and also as EMT-related genes in the literature.
Inference of the gene network of cancer EMT
From Takahashi et al.'s gene expression profile data, we estimated the gene network by the ARACNe algorithm. We used the gene expression profile data of the above selected genes. The ARACNe algorithm is a method that estimates a gene network from a gene expression profile observed by microarray. This method uses mutual information of gene expression profiles between any pair of two genes to eliminate the majority of indirect interactions often providing high apparent correlations. We executed 1000 times bootstrap, by using the ARACNe algorithm and chose the network links (regulations) with a significance level P < 1.0 × 10−10 and bootstrap value >90%.
Master regulator analysis and structural changes of the gene network during EMT
To extract structural changes of the gene network during cancer EMT, we applied master regulator analysis to the gene network estimated by ARACNe. In the master regulator analysis, most of the transcription factors (TF) in major TF databases (about 1800 TF) were investigated as to whether they regulate a significantly higher number of differentially expressed genes, than expected, in the network inferred by ARACNe. We used the Fisher exact test for this purpose with the significance level, P < 0.05. Visualization of the obtained gene network (transcriptional factor network) was conducted with Cytoscape (Smoot et al., 2011).
Supplementary material
Supplementary Material is available at Journal of Molecular Cell Biology online.
Funding
This work was supported by JSPS KAKENHI Grant-in-Aid for Scientific Research (B) Grant Number 25290070.
Conflict of interest: none declared.
Acknowledgements
We appreciate Prof. Saya of Keio University for providing detailed experimental information on the time-course of epithelial–mesenchymal transition of retina pigment epithelium. We also appreciate Prof. Nishibori of the International University of Health and Welfare and Ms Miwa for support in writing this article.
References
Author notes
These authors contributed equally to this work.